2026年山东省中考试卷精选九年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年山东省中考试卷精选九年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第52页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
19.(本小题满分 10 分)综合与实践
[活动背景]
数学活动课上,老师提供了如下素材:某窗户生产厂家要用一根长为 $6 m$ 的铝合金型材制作一个“日”字形窗户框架 $ABCD$(如图),要求恰好用完整条铝合金型材(接缝及型材宽度忽略不计).
[活动任务]
结合素材信息,运用所学数学知识,给出合理的窗户框架设计方案.
[方案一]
甲学习小组从美观角度出发,计划把窗户框架长宽之比设计为接近黄金分割比的 $5:3$.请帮助甲学习小组求出此时窗户框架的宽 $AB$.
[方案二]
乙学习小组从实用角度出发,计划把窗户面积设计得尽可能大,从而使采光效果更好.请帮助乙学习小组求出窗户的最大面积.
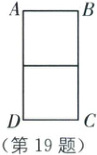
[活动背景]
数学活动课上,老师提供了如下素材:某窗户生产厂家要用一根长为 $6 m$ 的铝合金型材制作一个“日”字形窗户框架 $ABCD$(如图),要求恰好用完整条铝合金型材(接缝及型材宽度忽略不计).
[活动任务]
结合素材信息,运用所学数学知识,给出合理的窗户框架设计方案.
[方案一]
甲学习小组从美观角度出发,计划把窗户框架长宽之比设计为接近黄金分割比的 $5:3$.请帮助甲学习小组求出此时窗户框架的宽 $AB$.
[方案二]
乙学习小组从实用角度出发,计划把窗户面积设计得尽可能大,从而使采光效果更好.请帮助乙学习小组求出窗户的最大面积.

答案:
19.[解析]本题考查了二次函数在实际生活中的运用及求函数最值的方法.
解:[方案一]由题意,设窗户框架的宽AB为xm,AD长为ym.
$\because$“日”字形框架由3条横向边和2条纵向边组成,总型材长度为6m,
$\therefore 3x+2y=6.\because$长宽之比为$5:3$,
$\therefore y:x=5:3$,即$y=\frac{5}{3}x$.
将$y=\frac{5}{3}x$代入$3x+2y=6$,得$3x+2×\frac{5}{3}x=6$,解得$x=\frac{18}{19}$.
故窗户框架的宽AB为$\frac{18}{19}m$.
[方案二]由题意,设窗户框架的长AD为xm,则宽AB为$\frac{6-2x}{3}m,\therefore S=\frac{6-2x}{3}· x$,即$S=-\frac{2}{3}x^{2}+2x$,
$\therefore$要使窗户框架的面积最大,则$x=-\frac{2}{2×(-\frac{2}{3})}=1.5$,
于是宽为$\frac{6-2x}{3}=\frac{6-2×1.5}{3}=1(m)$,
$\therefore$当$x=1.5$时,S最大值为1.5,
$\therefore$要使做成的窗户面积最大,故该窗户框架的宽AB,长AD分别为1米,1.5米时,窗户的面积最大,最大值为$1.5m^{2}$.
解:[方案一]由题意,设窗户框架的宽AB为xm,AD长为ym.
$\because$“日”字形框架由3条横向边和2条纵向边组成,总型材长度为6m,
$\therefore 3x+2y=6.\because$长宽之比为$5:3$,
$\therefore y:x=5:3$,即$y=\frac{5}{3}x$.
将$y=\frac{5}{3}x$代入$3x+2y=6$,得$3x+2×\frac{5}{3}x=6$,解得$x=\frac{18}{19}$.
故窗户框架的宽AB为$\frac{18}{19}m$.
[方案二]由题意,设窗户框架的长AD为xm,则宽AB为$\frac{6-2x}{3}m,\therefore S=\frac{6-2x}{3}· x$,即$S=-\frac{2}{3}x^{2}+2x$,
$\therefore$要使窗户框架的面积最大,则$x=-\frac{2}{2×(-\frac{2}{3})}=1.5$,
于是宽为$\frac{6-2x}{3}=\frac{6-2×1.5}{3}=1(m)$,
$\therefore$当$x=1.5$时,S最大值为1.5,
$\therefore$要使做成的窗户面积最大,故该窗户框架的宽AB,长AD分别为1米,1.5米时,窗户的面积最大,最大值为$1.5m^{2}$.
20.(本小题满分 12 分)如图,$A(-6,0)$,$B(0,8)$,点 $M$ 在线段 $OB$ 上,将 $\triangle ABM$ 沿直线 $AM$ 折叠,点 $B$ 恰好落在点 $B'(a,0)$ 处.
(1)求 $a$ 的值;
(2)求直线 $AM$ 的表达式;
(3)若直线 $y=-x+t$ 与直线 $AM$ 的交点在直线 $x=a$ 的左侧,请直接写出 $t$ 的取值范围.

(1)求 $a$ 的值;
(2)求直线 $AM$ 的表达式;
(3)若直线 $y=-x+t$ 与直线 $AM$ 的交点在直线 $x=a$ 的左侧,请直接写出 $t$ 的取值范围.

答案:
20.[解析]本题考查了坐标与图形、勾股定理、解三角形、翻折的性质、一次函数的性质.
解:
(1)$\because A(-6,0),B(0,8)$,
$\therefore OA=6,OB=8.\because \angle AOB=90^{\circ}$,
$\therefore AB=\sqrt{OA^{2}+OB^{2}}=10$.
$\because$将$\triangle ABM$沿直线AM折叠,点B恰好落在点$B^{\prime}(a,0)$处,
$\therefore AB^{\prime}=AB=10$,
$\therefore OB^{\prime}=10-6=4,\therefore B^{\prime}(4,0)$,
$\therefore a=4$.
(2)设$OM=x$,根据折叠的性质,
得$BM=B^{\prime}M=8-x,AB=AB^{\prime}$.
由
(1),得$OB^{\prime}=4$.
$\because B^{\prime}M^{2}=OM^{2}+OB^{\prime2}$,
$\therefore (8-x)^{2}=4^{2}+x^{2}$,
解得$x=3$,故$M(0,3)$.
设直线AM的表达式为$y=kx+3$,
$\therefore -6k+3=0$,解得$k=\frac{1}{2}$.
故直线AM的表达式为$y=\frac{1}{2}x+3$.
(3)由
(1),得$a=4$,
$\therefore$直线$y=-x+t$与直线AM的交点在直线$x=4$的左侧.
如图,直线AM与直线$x=4$交于点N.

当$x=4$时,$y=\frac{1}{2}x+3=\frac{1}{2}×4+3=5,\therefore N(4,5)$.
$\because$直线$y=-x+t$与直线AM的交点在直线$x=a$的左侧,$\therefore$直线$y=-x+t$经过点N时恰好是临界点,
$\therefore 5=-4+t$,解得$t=9$,
$\therefore t$的取值范围为$t<9$.
20.[解析]本题考查了坐标与图形、勾股定理、解三角形、翻折的性质、一次函数的性质.
解:
(1)$\because A(-6,0),B(0,8)$,
$\therefore OA=6,OB=8.\because \angle AOB=90^{\circ}$,
$\therefore AB=\sqrt{OA^{2}+OB^{2}}=10$.
$\because$将$\triangle ABM$沿直线AM折叠,点B恰好落在点$B^{\prime}(a,0)$处,
$\therefore AB^{\prime}=AB=10$,
$\therefore OB^{\prime}=10-6=4,\therefore B^{\prime}(4,0)$,
$\therefore a=4$.
(2)设$OM=x$,根据折叠的性质,
得$BM=B^{\prime}M=8-x,AB=AB^{\prime}$.
由
(1),得$OB^{\prime}=4$.
$\because B^{\prime}M^{2}=OM^{2}+OB^{\prime2}$,
$\therefore (8-x)^{2}=4^{2}+x^{2}$,
解得$x=3$,故$M(0,3)$.
设直线AM的表达式为$y=kx+3$,
$\therefore -6k+3=0$,解得$k=\frac{1}{2}$.
故直线AM的表达式为$y=\frac{1}{2}x+3$.
(3)由
(1),得$a=4$,
$\therefore$直线$y=-x+t$与直线AM的交点在直线$x=4$的左侧.
如图,直线AM与直线$x=4$交于点N.

当$x=4$时,$y=\frac{1}{2}x+3=\frac{1}{2}×4+3=5,\therefore N(4,5)$.
$\because$直线$y=-x+t$与直线AM的交点在直线$x=a$的左侧,$\therefore$直线$y=-x+t$经过点N时恰好是临界点,
$\therefore 5=-4+t$,解得$t=9$,
$\therefore t$的取值范围为$t<9$.
查看更多完整答案,请扫码查看


