2026年山东省中考试卷精选九年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年山东省中考试卷精选九年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
21. (本小题满分 12 分)如图,某学校教学楼$AB$和市创业大厦$CD$之间矗立着一座小山.为了测得大厦的高度,小伟首先登至小山的最高处$E$,测得$B$,$D$处的俯角分别为$68.5°$,$27.7°$;然后操控无人机铅直起飞至比$E$处高$20 m$的$F$处.再次测得这两处的俯角分别为$70.8°$,$33.3°$.已知点$A$,$B$,$C$,$D$,$E$,$F$均在同一平面内,$AC$为水平地面,$AB = 12 m$.请求出大厦$CD$的高度(结果精确到$0.1 m$,参考数据见下表).


答案:
21.[解析]本题考查了解直角三角形的应用
通过作垂线补成矩形和三角形,然后利用三角形的边角关系和方程的思想来进行计算.
解:如图,延长AB交过点E,F的水平线于点G,H,延长CD交过点E,F的水平线于点M,N.

在Rt△EGB中,设GB=xm.
又tan∠GEB=$\frac{GB}{GE}$,
∴GE=$\frac{GB}{tan68.5°}$≈$\frac{x}{2.54}$.
在Rt△FHB中,tan∠HFB=$\frac{HB}{HF}$,
∴HF=$\frac{HB}{tan70.8°}$≈$\frac{x+20}{2.87}$.
∵GE=HF,
∴$\frac{x}{2.54}$=$\frac{x+20}{2.87}$,
解得x≈153.9(m),
∴GB=153.9m,
∴AH=AB+GH+GB=12+20+153.9=185.9(m).
∵在Rt△EMD中,设MD=ym.
又tan∠MED=$\frac{MD}{ME}$,
∴ME=$\frac{MD}{tan27.7°}$≈$\frac{y}{0.53}$.
∵在Rt△NFD中,tan∠NFD=$\frac{DN}{FN}$,
∴FN=$\frac{DN+20}{tan33.3°}$≈$\frac{y+20}{0.66}$.
∵ME=FN,
∴$\frac{y}{0.53}$=$\frac{y+20}{0.66}$,
解得y≈81.5(m),
∴MD=81.5m,
∴CN=CD+MD+MN=CD+81.5+20,即CN=CD+101.5.
∵AH=CN,
∴CD+101.5=185.9,
∴CD=84.4m.
故大厦CD的高度约为84.4米.
21.[解析]本题考查了解直角三角形的应用
通过作垂线补成矩形和三角形,然后利用三角形的边角关系和方程的思想来进行计算.
解:如图,延长AB交过点E,F的水平线于点G,H,延长CD交过点E,F的水平线于点M,N.

在Rt△EGB中,设GB=xm.
又tan∠GEB=$\frac{GB}{GE}$,
∴GE=$\frac{GB}{tan68.5°}$≈$\frac{x}{2.54}$.
在Rt△FHB中,tan∠HFB=$\frac{HB}{HF}$,
∴HF=$\frac{HB}{tan70.8°}$≈$\frac{x+20}{2.87}$.
∵GE=HF,
∴$\frac{x}{2.54}$=$\frac{x+20}{2.87}$,
解得x≈153.9(m),
∴GB=153.9m,
∴AH=AB+GH+GB=12+20+153.9=185.9(m).
∵在Rt△EMD中,设MD=ym.
又tan∠MED=$\frac{MD}{ME}$,
∴ME=$\frac{MD}{tan27.7°}$≈$\frac{y}{0.53}$.
∵在Rt△NFD中,tan∠NFD=$\frac{DN}{FN}$,
∴FN=$\frac{DN+20}{tan33.3°}$≈$\frac{y+20}{0.66}$.
∵ME=FN,
∴$\frac{y}{0.53}$=$\frac{y+20}{0.66}$,
解得y≈81.5(m),
∴MD=81.5m,
∴CN=CD+MD+MN=CD+81.5+20,即CN=CD+101.5.
∵AH=CN,
∴CD+101.5=185.9,
∴CD=84.4m.
故大厦CD的高度约为84.4米.
22. (本小题满分 13 分)如图,一条抛物线$y = ax^2 + bx + \frac{5}{2}$与$x$轴相交于$A(-1,0)$,$B(5,0)$两点,与$y$轴相交于点$C$.
(1)求抛物线对应的函数表达式.
(2)问在抛物线上是否存在点$P$,使得$\angle ABC = \frac{1}{2} \angle PAB$? 若存在,求出点$P$的坐标;若不存在,说明理由.
(3)将射线$CB$绕点$C$逆时针旋转一定角度,使其恰
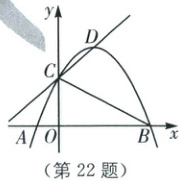
①求旋转角度的正切值.
②当$\angle CQM = 90°$时,求原抛物线平移的距离.
(1)求抛物线对应的函数表达式.
(2)问在抛物线上是否存在点$P$,使得$\angle ABC = \frac{1}{2} \angle PAB$? 若存在,求出点$P$的坐标;若不存在,说明理由.
(3)将射线$CB$绕点$C$逆时针旋转一定角度,使其恰
好
经
过
抛
物线的顶点$D$,再将抛物线沿直线$CD$平移,得到一条新的抛物线(其顶点为$M$).设这两条抛物线的交点为$Q$.
①求旋转角度的正切值.
②当$\angle CQM = 90°$时,求原抛物线平移的距离.
答案:
22.[解析]本题考查了二次函数与几何的综合题.
(1)利用待定系数法求函数的表达式;
(2)由于有半角关系,考虑构造等腰三角形,利用两个一次函数平行的关系以及对称的性质求出点P的坐标;
(3)①利用一次函数的平行的关系以及等积法、勾股定理、正切的定义进行计算;
②根据平移的关系求出平移后的抛物线,联立两个抛物线的表达式求出点Q坐标,作QK⊥y轴,ML⊥QK 交KQ的延长线于点L,再利用相似三角形的判定和性质来进行计算.
解:
(1)抛物线y=ax²+bx+$\frac{5}{2}$与x轴相交于A(−1,0),B(5,0)两点,将两点坐标代入抛物线,
得$\begin{cases} a×(−1)²+b×(−1)+\frac{5}{2}=0, \\ a×5²+b×5+\frac{5}{2}=0, \end{cases}$
解$\begin{cases} a=−\frac{1}{2}, \\ b=2, \end{cases}$
∴抛物线的表达式y=−$\frac{1}{2}$x²+2.x+$\frac{5}{2}$.
(2)
∵y=−$\frac{1}{2}$x²+2x+$\frac{5}{2}$,
∴当x=0时,y=$\frac{5}{2}$
∴C(0,$\frac{5}{2}$).如图
(1),作BC的中垂线交x轴于点E,连接CE,则CE=BE,

∴∠ECB=∠ABC,
∴∠AEC=∠ABC+∠BCE=2∠ABC.
∵B(5,0),C(0,$\frac{5}{2}$),
∴OB=5,OC=$\frac{5}{2}$.
设OE=m,则CE=BE=5−m.
在Rt△COE中,由勾股定理,得m²+($\frac{5}{2}$)²=(5−m)²,
解得m=$\frac{15}{8}$,
∴E($\frac{15}{8}$,0).
设直线CE的表达式为y=kx+$\frac{5}{2}$.把E($\frac{15}{8}$,0)代入,得0=$\frac{15}{8}$k+$\frac{5}{2}$,解得k=−$\frac{4}{3}$,
∴y=−$\frac{4}{3}$x+$\frac{5}{2}$.
过点A作AP₁//CE,交y轴于点F,交抛物线于点P₁,
则∠P₁AB=∠CEA=2∠ABC.设直线AP₁的表达式为y=−$\frac{4}{3}$x+n.把A(−1,0)代人,得0=−$\frac{4}{3}$×(−1)+n,
解得n=−$\frac{4}{3}$,则y=−$\frac{4}{3}$x−$\frac{4}{3}$.
联立
$\begin{cases} y=−\frac{1}{2}x²+2x+\frac{5}{2}, \\ y=−\frac{4}{3}x−\frac{4}{3}, \end{cases}$
解得$\begin{cases} x=\frac{23}{3}, \\ y=−\frac{104}{9} \end{cases}$或$\begin{cases} x=−1, \\ y=0 \end{cases}$
∴P₁($\frac{23}{3}$,−$\frac{104}{9}$)
∵y=−$\frac{4}{3}$x−$\frac{4}{3}$,
∴当x=0时,y=−$\frac{4}{3}$,
∴F(0,−$\frac{4}{3}$),
作点F关于x轴的对称点G,连接AG,交抛物线于点P₂,则点G(0,$\frac{4}{3}$),∠GAB=2∠ABC,
∴直线AG与抛物线的交点也满足题意.
同法,可得直线AG的表达式为y=
$\frac{4}{3}$x+$\frac{4}{3}$.
联立
$\begin{cases} y=\frac{4}{3}x+\frac{4}{3}, \\ y=−\frac{1}{2}x²+2x+\frac{5}{2}, \end{cases}$
解得$\begin{cases} x=\frac{7}{3}, \\ y=\frac{40}{9} \end{cases}$或$\begin{cases} x=−1, \\ y=0 \end{cases}$
∴P₂($\frac{7}{3}$,$\frac{40}{9}$).
综上所述,存在点P,且P($\frac{23}{3}$,−$\frac{104}{9}$)或P($\frac{7}{3}$,$\frac{40}{9}$).
(3)①
∵y=−$\frac{1}{2}$x²+2x+$\frac{5}{2}$=
−$\frac{1}{2}$(x−2)²+$\frac{9}{2}$,
∴D(2,$\frac{9}{2}$),C(0,$\frac{5}{2}$),
同法,可得直线CD的表达式为y=
x+$\frac{5}{2}$.
如图
(2),由题意,得∠BCD即为旋转角,连接BC,作BE//CD,交y轴于点E,作CF⊥BE于点F,则∠CBF=
∠BCD,

∴tan∠CBF=tan∠BCD,
同法,可得直线BE的表达式为y=
x−5,
∴当x=0时,y=−5,
∴E(0,−5),
∴OE=OB=5,CE=5+$\frac{5}{2}$=$\frac{15}{2}$,
∴BE=5$\sqrt{2}$.
∵S△BCE=$\frac{1}{2}$BE·CF=$\frac{1}{2}$CE·OB,
∴5$\sqrt{2}$CF=5×$\frac{15}{2}$,
∴CF=$\frac{15\sqrt{2}}{4}$.
∵BC= $\sqrt{5²+(\frac{5}{2})²}$=$\frac{5\sqrt{5}}{2}$,
∴BF= $\sqrt{BC²−CF²}$=$\frac{5\sqrt{2}}{4}$,
∴tan∠BCD=tan∠CBF=$\frac{CF}{BF}$=3.②将抛物线沿直线CD平移,等同于将抛物线沿直线BE平移.
∵OB=OE,
∴抛物线在水平方向和竖直方向上的移动距离相等.
设将抛物线向右和向上分别平移t(t>0)个单位,得到新的抛物线,
则新抛物线的表达式为y=−$\frac{1}{2}$(x−2−t)²+$\frac{9}{2}$+t,
∴M(2+t,$\frac{9}{2}$+t).
联立
$\begin{cases} y=−\frac{1}{2}(x−2−t)²+\frac{9}{2}+t, \\ y=−\frac{1}{2}(x−2)²+\frac{9}{2}, \end{cases}$
解得
$\begin{cases} x=\frac{t+2}{2}, \\ y=−\frac{t²}{8}+\frac{t}{2}+4, \end{cases}$
∴Q($\frac{t+2}{2}$,−$\frac{t²}{8}$+$\frac{t}{2}$+4).
如图
(3),作QK⊥y轴,ML⊥QK交KQ的延长线于点L,
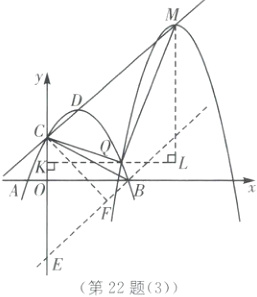
∴∠CKQ=∠MLQ=90°=∠CQM,
CK=$\frac{5}{2}$+$\frac{t²}{8}$+$\frac{t}{2}$−4=$\frac{t²}{8}$+$\frac{t}{2}$−$\frac{3}{2}$,QK=$\frac{t+2}{2}$,QL=2+t−$\frac{t+2}{2}$=$\frac{t+2}{2}$,
ML=$\frac{9}{2}$+t+$\frac{t²}{8}$+$\frac{t}{2}$−4=$\frac{t²}{8}$+$\frac{t}{2}$+$\frac{1}{2}$,
∴∠CQK=∠QML=90°−∠MQL,
∴△CQK∽△QML,
∴$\frac{CK}{QL}$=$\frac{QK}{ML}$,
∴CK·ML=QL·QK,
∴($\frac{t²}{8}$+$\frac{t}{2}$−$\frac{3}{2}$)·($\frac{t²}{8}$+$\frac{t}{2}$+$\frac{1}{2}$)=($\frac{t+2}{2}$)²,
解得t=2+4$\sqrt{2}$或t=−2(舍去)或t=2−4$\sqrt{2}$(舍去),
∴抛物线在水平方向和竖直方向的平移距离均为2+4√2,
∴抛物线的平移距离为$\sqrt{2}$×(2+4$\sqrt{2}$)=2$\sqrt{2}$+8.
当抛物线沿直线CD向下移动时,同理,可得抛物线的平移距离为$\sqrt{2}$×(2+4$\sqrt{2}$)=2$\sqrt{2}$+8.
综上所述,抛物线的平移距离为2$\sqrt{2}$+8.
方法诠释 对于倍角或半角的关系,我们需要通过作中垂线构造等腰三角形,从而得到相等的角,然后利用一次函数平行的关系来解决问题
22.[解析]本题考查了二次函数与几何的综合题.
(1)利用待定系数法求函数的表达式;
(2)由于有半角关系,考虑构造等腰三角形,利用两个一次函数平行的关系以及对称的性质求出点P的坐标;
(3)①利用一次函数的平行的关系以及等积法、勾股定理、正切的定义进行计算;
②根据平移的关系求出平移后的抛物线,联立两个抛物线的表达式求出点Q坐标,作QK⊥y轴,ML⊥QK 交KQ的延长线于点L,再利用相似三角形的判定和性质来进行计算.
解:
(1)抛物线y=ax²+bx+$\frac{5}{2}$与x轴相交于A(−1,0),B(5,0)两点,将两点坐标代入抛物线,
得$\begin{cases} a×(−1)²+b×(−1)+\frac{5}{2}=0, \\ a×5²+b×5+\frac{5}{2}=0, \end{cases}$
解$\begin{cases} a=−\frac{1}{2}, \\ b=2, \end{cases}$
∴抛物线的表达式y=−$\frac{1}{2}$x²+2.x+$\frac{5}{2}$.
(2)
∵y=−$\frac{1}{2}$x²+2x+$\frac{5}{2}$,
∴当x=0时,y=$\frac{5}{2}$
∴C(0,$\frac{5}{2}$).如图
(1),作BC的中垂线交x轴于点E,连接CE,则CE=BE,

∴∠ECB=∠ABC,
∴∠AEC=∠ABC+∠BCE=2∠ABC.
∵B(5,0),C(0,$\frac{5}{2}$),
∴OB=5,OC=$\frac{5}{2}$.
设OE=m,则CE=BE=5−m.
在Rt△COE中,由勾股定理,得m²+($\frac{5}{2}$)²=(5−m)²,
解得m=$\frac{15}{8}$,
∴E($\frac{15}{8}$,0).
设直线CE的表达式为y=kx+$\frac{5}{2}$.把E($\frac{15}{8}$,0)代入,得0=$\frac{15}{8}$k+$\frac{5}{2}$,解得k=−$\frac{4}{3}$,
∴y=−$\frac{4}{3}$x+$\frac{5}{2}$.
过点A作AP₁//CE,交y轴于点F,交抛物线于点P₁,
则∠P₁AB=∠CEA=2∠ABC.设直线AP₁的表达式为y=−$\frac{4}{3}$x+n.把A(−1,0)代人,得0=−$\frac{4}{3}$×(−1)+n,
解得n=−$\frac{4}{3}$,则y=−$\frac{4}{3}$x−$\frac{4}{3}$.
联立
$\begin{cases} y=−\frac{1}{2}x²+2x+\frac{5}{2}, \\ y=−\frac{4}{3}x−\frac{4}{3}, \end{cases}$
解得$\begin{cases} x=\frac{23}{3}, \\ y=−\frac{104}{9} \end{cases}$或$\begin{cases} x=−1, \\ y=0 \end{cases}$
∴P₁($\frac{23}{3}$,−$\frac{104}{9}$)
∵y=−$\frac{4}{3}$x−$\frac{4}{3}$,
∴当x=0时,y=−$\frac{4}{3}$,
∴F(0,−$\frac{4}{3}$),
作点F关于x轴的对称点G,连接AG,交抛物线于点P₂,则点G(0,$\frac{4}{3}$),∠GAB=2∠ABC,
∴直线AG与抛物线的交点也满足题意.
同法,可得直线AG的表达式为y=
$\frac{4}{3}$x+$\frac{4}{3}$.
联立
$\begin{cases} y=\frac{4}{3}x+\frac{4}{3}, \\ y=−\frac{1}{2}x²+2x+\frac{5}{2}, \end{cases}$
解得$\begin{cases} x=\frac{7}{3}, \\ y=\frac{40}{9} \end{cases}$或$\begin{cases} x=−1, \\ y=0 \end{cases}$
∴P₂($\frac{7}{3}$,$\frac{40}{9}$).
综上所述,存在点P,且P($\frac{23}{3}$,−$\frac{104}{9}$)或P($\frac{7}{3}$,$\frac{40}{9}$).
(3)①
∵y=−$\frac{1}{2}$x²+2x+$\frac{5}{2}$=
−$\frac{1}{2}$(x−2)²+$\frac{9}{2}$,
∴D(2,$\frac{9}{2}$),C(0,$\frac{5}{2}$),
同法,可得直线CD的表达式为y=
x+$\frac{5}{2}$.
如图
(2),由题意,得∠BCD即为旋转角,连接BC,作BE//CD,交y轴于点E,作CF⊥BE于点F,则∠CBF=
∠BCD,

∴tan∠CBF=tan∠BCD,
同法,可得直线BE的表达式为y=
x−5,
∴当x=0时,y=−5,
∴E(0,−5),
∴OE=OB=5,CE=5+$\frac{5}{2}$=$\frac{15}{2}$,
∴BE=5$\sqrt{2}$.
∵S△BCE=$\frac{1}{2}$BE·CF=$\frac{1}{2}$CE·OB,
∴5$\sqrt{2}$CF=5×$\frac{15}{2}$,
∴CF=$\frac{15\sqrt{2}}{4}$.
∵BC= $\sqrt{5²+(\frac{5}{2})²}$=$\frac{5\sqrt{5}}{2}$,
∴BF= $\sqrt{BC²−CF²}$=$\frac{5\sqrt{2}}{4}$,
∴tan∠BCD=tan∠CBF=$\frac{CF}{BF}$=3.②将抛物线沿直线CD平移,等同于将抛物线沿直线BE平移.
∵OB=OE,
∴抛物线在水平方向和竖直方向上的移动距离相等.
设将抛物线向右和向上分别平移t(t>0)个单位,得到新的抛物线,
则新抛物线的表达式为y=−$\frac{1}{2}$(x−2−t)²+$\frac{9}{2}$+t,
∴M(2+t,$\frac{9}{2}$+t).
联立
$\begin{cases} y=−\frac{1}{2}(x−2−t)²+\frac{9}{2}+t, \\ y=−\frac{1}{2}(x−2)²+\frac{9}{2}, \end{cases}$
解得
$\begin{cases} x=\frac{t+2}{2}, \\ y=−\frac{t²}{8}+\frac{t}{2}+4, \end{cases}$
∴Q($\frac{t+2}{2}$,−$\frac{t²}{8}$+$\frac{t}{2}$+4).
如图
(3),作QK⊥y轴,ML⊥QK交KQ的延长线于点L,

∴∠CKQ=∠MLQ=90°=∠CQM,
CK=$\frac{5}{2}$+$\frac{t²}{8}$+$\frac{t}{2}$−4=$\frac{t²}{8}$+$\frac{t}{2}$−$\frac{3}{2}$,QK=$\frac{t+2}{2}$,QL=2+t−$\frac{t+2}{2}$=$\frac{t+2}{2}$,
ML=$\frac{9}{2}$+t+$\frac{t²}{8}$+$\frac{t}{2}$−4=$\frac{t²}{8}$+$\frac{t}{2}$+$\frac{1}{2}$,
∴∠CQK=∠QML=90°−∠MQL,
∴△CQK∽△QML,
∴$\frac{CK}{QL}$=$\frac{QK}{ML}$,
∴CK·ML=QL·QK,
∴($\frac{t²}{8}$+$\frac{t}{2}$−$\frac{3}{2}$)·($\frac{t²}{8}$+$\frac{t}{2}$+$\frac{1}{2}$)=($\frac{t+2}{2}$)²,
解得t=2+4$\sqrt{2}$或t=−2(舍去)或t=2−4$\sqrt{2}$(舍去),
∴抛物线在水平方向和竖直方向的平移距离均为2+4√2,
∴抛物线的平移距离为$\sqrt{2}$×(2+4$\sqrt{2}$)=2$\sqrt{2}$+8.
当抛物线沿直线CD向下移动时,同理,可得抛物线的平移距离为$\sqrt{2}$×(2+4$\sqrt{2}$)=2$\sqrt{2}$+8.
综上所述,抛物线的平移距离为2$\sqrt{2}$+8.
方法诠释 对于倍角或半角的关系,我们需要通过作中垂线构造等腰三角形,从而得到相等的角,然后利用一次函数平行的关系来解决问题
查看更多完整答案,请扫码查看


