2026年山东省中考试卷精选九年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年山东省中考试卷精选九年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第21页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
18. (本小题满分 7 分)2025 年 4 月 19 日,烟台市民文化艺术季启幕. 某校带领甲、乙两个社团参观甲骨学发展史馆,领略殷商文明甲骨文化穿越千年的不朽魅力. 活动结束后,两个社团进行了一次满分为 10 分的甲骨学发展史测试,并对所有学生的成绩进行了收集、整理、分析,信息如下:
①甲社团的成绩(单位:分)情况如下:
6,6,6,6,7,7,7,6,7,6,7,8,8,8,8,9,8,9,9,8,9,9,9,7,9,6,9,9,10,8,8,9,9,10,10.
②乙社团的平均成绩为$\frac{6 × 8+7 × 12+8 × 6+9 × 10+10 × 4}{8+12+6+10+4}=7.75$(分).
③将两个社团的成绩绘制成如下不完整的统计图.
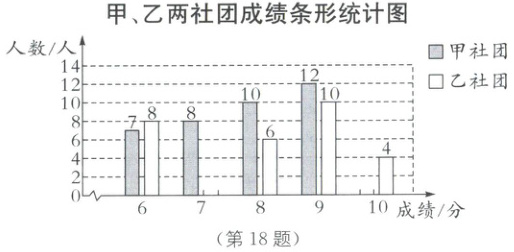
根据以上信息,解决下列问题:
(1)将条形统计图补充完整;
(2)成绩为 8 分的学生在
(3)已知甲社团的满分学生中有两名女生,现从甲社团满分学生中随机抽取两人,参加甲骨学发展史宣讲活动.请用树状图或表格求所抽取的两人恰好是一名男生和一名女生的概率.
①甲社团的成绩(单位:分)情况如下:
6,6,6,6,7,7,7,6,7,6,7,8,8,8,8,9,8,9,9,8,9,9,9,7,9,6,9,9,10,8,8,9,9,10,10.
②乙社团的平均成绩为$\frac{6 × 8+7 × 12+8 × 6+9 × 10+10 × 4}{8+12+6+10+4}=7.75$(分).
③将两个社团的成绩绘制成如下不完整的统计图.

根据以上信息,解决下列问题:
(1)将条形统计图补充完整;
(2)成绩为 8 分的学生在
乙
社团的排名更靠前(填“甲”或“乙”);(3)已知甲社团的满分学生中有两名女生,现从甲社团满分学生中随机抽取两人,参加甲骨学发展史宣讲活动.请用树状图或表格求所抽取的两人恰好是一名男生和一名女生的概率.
答案:
18.[解析]本题考查了从统计数据、平均数公式中获取信息,求解中位数,利用中位数做决策,利用画树状图法或列表法求解随机事件的概率. 解:
(1)由统计数据知,甲社团满分人数为3人,乙社团7分的有12人,补全图形如图
(1). 甲、乙两社团成绩条形统计图
(2)甲社团成绩的中位数为$\frac{8 + 8}{2} = 8$(分),乙社团成绩的中位数为$\frac{7 + 8}{2} = 7.5$(分), 所以成绩为8分的学生在乙社团的排名更靠前.
(3)男生用A表示,两名女生分别用B和C表示,如图
(2). 由图可知共有6种可能的结果,且每种结果出现的可能性相同,其中恰好抽到一名男生和一名女生有4种结果,所以所抽取的两人恰好是一名男生和一名女生的概率为$\frac{4}{6} = \frac{2}{3}$.
由图可知共有6种可能的结果,且每种结果出现的可能性相同,其中恰好抽到一名男生和一名女生有4种结果,所以所抽取的两人恰好是一名男生和一名女生的概率为$\frac{4}{6} = \frac{2}{3}$.
18.[解析]本题考查了从统计数据、平均数公式中获取信息,求解中位数,利用中位数做决策,利用画树状图法或列表法求解随机事件的概率. 解:
(1)由统计数据知,甲社团满分人数为3人,乙社团7分的有12人,补全图形如图
(1). 甲、乙两社团成绩条形统计图

(2)甲社团成绩的中位数为$\frac{8 + 8}{2} = 8$(分),乙社团成绩的中位数为$\frac{7 + 8}{2} = 7.5$(分), 所以成绩为8分的学生在乙社团的排名更靠前.
(3)男生用A表示,两名女生分别用B和C表示,如图
(2).
 由图可知共有6种可能的结果,且每种结果出现的可能性相同,其中恰好抽到一名男生和一名女生有4种结果,所以所抽取的两人恰好是一名男生和一名女生的概率为$\frac{4}{6} = \frac{2}{3}$.
由图可知共有6种可能的结果,且每种结果出现的可能性相同,其中恰好抽到一名男生和一名女生有4种结果,所以所抽取的两人恰好是一名男生和一名女生的概率为$\frac{4}{6} = \frac{2}{3}$. 19. (本小题满分 7 分)如图,$BD$ 是矩形 $ABCD$ 的对角线,请按以下要求解决问题:
(1)利用尺规作$\triangle BED$,使$\triangle BED$与$\triangle BCD$关于直线 $BD$ 成轴对称(不写作法,保留作图痕迹);
(2)在(1)的条件下,若 $BE$ 交 $AD$ 于点 $F$,$AB=1$,$BC=2$,求 $AF$ 的长.

(1)利用尺规作$\triangle BED$,使$\triangle BED$与$\triangle BCD$关于直线 $BD$ 成轴对称(不写作法,保留作图痕迹);
(2)在(1)的条件下,若 $BE$ 交 $AD$ 于点 $F$,$AB=1$,$BC=2$,求 $AF$ 的长.

答案:
19.[解析]本题考查的是作轴对称图形、全等三角形的判定与性质、矩形的性质、勾股定理的应用. 解:
(1)如图,$\triangle BED$即为所求作的三角形. $\because$由作图可得$DE = DC$,$BE = BC$,$BD = BD$,$\therefore \triangle BCD \cong \triangle BED$(SSS), $\therefore \triangle BED$即为所求作的三角形.
$\because$由作图可得$DE = DC$,$BE = BC$,$BD = BD$,$\therefore \triangle BCD \cong \triangle BED$(SSS), $\therefore \triangle BED$即为所求作的三角形.
(2)$\because$四边形ABCD为矩形, $\therefore AD = BC = 2$,$AB = CD = 1$, $AD // BC$,$\angle A = 90°$, $\therefore \angle ADB = \angle CBD$. $\because \angle EBD = \angle CBD$, $\therefore \angle FBD = \angle FDB$, $\therefore FB = FD$,设$AF = x$,则$DF = 2 - x$,$1^2 + x^2 = (2 - x)^2$, 解得$x = \frac{3}{4}$,$\therefore AF = \frac{3}{4}$
19.[解析]本题考查的是作轴对称图形、全等三角形的判定与性质、矩形的性质、勾股定理的应用. 解:
(1)如图,$\triangle BED$即为所求作的三角形.
 $\because$由作图可得$DE = DC$,$BE = BC$,$BD = BD$,$\therefore \triangle BCD \cong \triangle BED$(SSS), $\therefore \triangle BED$即为所求作的三角形.
$\because$由作图可得$DE = DC$,$BE = BC$,$BD = BD$,$\therefore \triangle BCD \cong \triangle BED$(SSS), $\therefore \triangle BED$即为所求作的三角形. (2)$\because$四边形ABCD为矩形, $\therefore AD = BC = 2$,$AB = CD = 1$, $AD // BC$,$\angle A = 90°$, $\therefore \angle ADB = \angle CBD$. $\because \angle EBD = \angle CBD$, $\therefore \angle FBD = \angle FDB$, $\therefore FB = FD$,设$AF = x$,则$DF = 2 - x$,$1^2 + x^2 = (2 - x)^2$, 解得$x = \frac{3}{4}$,$\therefore AF = \frac{3}{4}$
20. (本小题满分 8 分)2025 年 6 月 5 日是第 54 个“世界环境日”,为打造绿色低碳社区,某社区决定购买甲、乙两种太阳能路灯安装在社区公共区域,升级改造现有照明系统. 已知购买 1 盏甲种路灯和 2 盏乙种路灯共需 220 元,购买 3 盏甲种路灯比 4 盏乙种路灯的费用少 140 元.
(1)求甲、乙两种路灯的单价;
(2)该社区计划购买甲、乙两种路灯共 40 盏,且甲种路灯的数量不超过乙种路灯数量的$\frac{1}{3}$,请通过计算设计一种购买方案,使所需费用最少.
(1)求甲、乙两种路灯的单价;
(2)该社区计划购买甲、乙两种路灯共 40 盏,且甲种路灯的数量不超过乙种路灯数量的$\frac{1}{3}$,请通过计算设计一种购买方案,使所需费用最少.
答案:
20.[解析]本题考查了二元一次方程组的应用、一元一次不等式的应用以及一次函数的应用.
(1)找准等量关系,正确列出二元一次方程组;
(2)根据各数量之间的关系,找出$w$关于$m$的函数关系式. 解:
(1)设甲种路灯的单价是$x$元,乙种路灯的单价是$y$元, 根据题意可得$\begin{cases}x + 2y = 220 \\4y - 3x = 140 \end{cases}$, 解得$\begin{cases}x = 60 \\y = 80 \end{cases}$. 故甲种路灯的单价是60元,乙种路灯的单价是80元.
(2)设购买$m$盏甲种路灯,该社区购买甲、乙两种路灯共花费$w$元,则购买$(40 - m)$盏乙种路灯, 根据题意可得$w = 60m + 80(40 - m) = -20m + 3200$. $\because -20 < 0$, $\therefore w$随$m$的增大而减小. 又$m \leq \frac{1}{3}(40 - m)$, $\therefore m \leq 10$, $\therefore$当$m = 10$时,$w$取得最小值,此时$40 - m = 40 - 10 = 30$(盏). 故当购买10盏甲种路灯,30盏乙种路灯时,所需费用最少.
(1)找准等量关系,正确列出二元一次方程组;
(2)根据各数量之间的关系,找出$w$关于$m$的函数关系式. 解:
(1)设甲种路灯的单价是$x$元,乙种路灯的单价是$y$元, 根据题意可得$\begin{cases}x + 2y = 220 \\4y - 3x = 140 \end{cases}$, 解得$\begin{cases}x = 60 \\y = 80 \end{cases}$. 故甲种路灯的单价是60元,乙种路灯的单价是80元.
(2)设购买$m$盏甲种路灯,该社区购买甲、乙两种路灯共花费$w$元,则购买$(40 - m)$盏乙种路灯, 根据题意可得$w = 60m + 80(40 - m) = -20m + 3200$. $\because -20 < 0$, $\therefore w$随$m$的增大而减小. 又$m \leq \frac{1}{3}(40 - m)$, $\therefore m \leq 10$, $\therefore$当$m = 10$时,$w$取得最小值,此时$40 - m = 40 - 10 = 30$(盏). 故当购买10盏甲种路灯,30盏乙种路灯时,所需费用最少.
查看更多完整答案,请扫码查看


