2026年山东省中考试卷精选九年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年山东省中考试卷精选九年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第13页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
1. -6 的相反数为(
A.-6
B.6
C.$-\frac{1}{6}$
D.$\frac{1}{6}$
B
).A.-6
B.6
C.$-\frac{1}{6}$
D.$\frac{1}{6}$
答案:
1.B [解析]本题考查了相反数的概念.
−6的相反数是6.故选B.
−6的相反数是6.故选B.
2. 围棋是中华民族发明的博弈活动.下列用棋子摆放的图形中,既是轴对称图形,又是中心对称图形的是(

D
).
答案:
2.D [解析]本题考查了中心对称图形、轴对称图形.
A.是轴对称图形,不是中心对称图形,不符合题意;
B.不是轴对称图形,是中心对称图形,不符合题意;
C.既不是轴对称图形,也不是中心对称图形,不符合题意;
D.既是轴对称图形,又是中心对称图形,符合题意.
故选D.
知识拓展 课本范围内,轴对称图形有线段、角(平角以内)、两直线相交、等腰三角形、正n边形、矩形、菱形、等腰梯形、圆、扇形;中心对称图形有线段、两直线相交、正n边形(n为偶数)、平行四边形、矩形、菱形、圆.
A.是轴对称图形,不是中心对称图形,不符合题意;
B.不是轴对称图形,是中心对称图形,不符合题意;
C.既不是轴对称图形,也不是中心对称图形,不符合题意;
D.既是轴对称图形,又是中心对称图形,符合题意.
故选D.
知识拓展 课本范围内,轴对称图形有线段、角(平角以内)、两直线相交、等腰三角形、正n边形、矩形、菱形、等腰梯形、圆、扇形;中心对称图形有线段、两直线相交、正n边形(n为偶数)、平行四边形、矩形、菱形、圆.
3. 2025 年 5 月,我国在西昌卫星发射中心成功将行星探测工程天问二号探测器发射升空,天问二号探测器将对小行星 2016HO3 和主带彗星 311P 开启科学探测,其中一个目标所在轨道与太阳间距将达到 3.74 亿公里.3.74 亿$=374 000 000$,将 374 000 000 用科学记数法表示为(
A.$0.374×10^{9}$
B.$3.74×10^{8}$
C.$3.74×10^{7}$
D.$374×10^{6}$
B
).A.$0.374×10^{9}$
B.$3.74×10^{8}$
C.$3.74×10^{7}$
D.$374×10^{6}$
答案:
3.B [解析]本题考查了科学记数法的表示方法.
3740000000=3.74×10⁸.故选B.
3740000000=3.74×10⁸.故选B.
4. 如图(1),榫卯是古代中国建筑、家具及其他器械的主要结构方式.图(2)的左视图是(

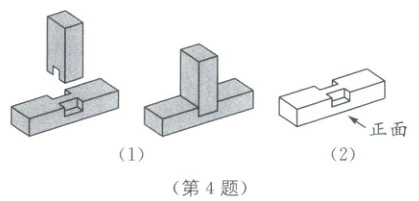
A
).

答案:
4.A [解析]本题考查了简单组合体的三视图,掌握组合体的三视图是解题的关键
从左边看,左视图如图.
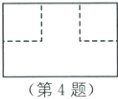
故选A.
4.A [解析]本题考查了简单组合体的三视图,掌握组合体的三视图是解题的关键
从左边看,左视图如图.

故选A.
5. 如图,在平面直角坐标系中,点 A,B,C 都在格点上,将$\triangle ABC$关于 y 轴的对称图形绕原点 O 旋转$180^{\circ}$,得到$\triangle A_{1}B_{1}C_{1}$,则点 A 的对应点$A_{1}$的坐标是(
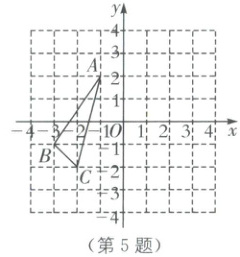
A.$(-1,-2)$
B.$(1,2)$
C.$(2,1)$
D.$(-2,-1)$
A
).
A.$(-1,-2)$
B.$(1,2)$
C.$(2,1)$
D.$(-2,-1)$
答案:
5.A[解析]本题考查了平面直角坐标系中点的变换,熟练掌握点的对称与旋转是解决本题的关键.
∵在平面直角坐标系中,点A(−1,2),
∴点A关于y轴对称的点为A₂(1,2).
又将点A₂(1,2)绕原点O旋转180°得到A₁,如图,可知点A₁(−1,−2).

故选A.
5.A[解析]本题考查了平面直角坐标系中点的变换,熟练掌握点的对称与旋转是解决本题的关键.
∵在平面直角坐标系中,点A(−1,2),
∴点A关于y轴对称的点为A₂(1,2).
又将点A₂(1,2)绕原点O旋转180°得到A₁,如图,可知点A₁(−1,−2).

故选A.
6. 下列计算正确的是(
A.$x^{2}+x^{3}=x^{5}$
B.$x^{2}· x^{3}=x^{6}$
C.$(2xy)^{2}=2x^{2}y^{2}$
D.$x^{8}÷ x^{4}=x^{4}$
D
).A.$x^{2}+x^{3}=x^{5}$
B.$x^{2}· x^{3}=x^{6}$
C.$(2xy)^{2}=2x^{2}y^{2}$
D.$x^{8}÷ x^{4}=x^{4}$
答案:
6.D [解析]本题考查了同底数幂的乘法及除法、合并同类项、积的乘方.
x²与x³不是同类项,无法合并,则A不符合题意;
x²·x³=x⁵,则B不符合题意;
(2xy)²=4x²y²,则C不符合题意;x⁸÷x⁴=x⁴,则D符合题意.
故选D.
x²与x³不是同类项,无法合并,则A不符合题意;
x²·x³=x⁵,则B不符合题意;
(2xy)²=4x²y²,则C不符合题意;x⁸÷x⁴=x⁴,则D符合题意.
故选D.
7. 如图,四边形$ABCD$是$\odot O$的内接四边形,$\angle ADC=90^{\circ}$,$DC=BC$,直线$EA$与$\odot O$相切于点$A$.若$\angle BCD=128^{\circ}$,则$\angle DAE$的度数为(
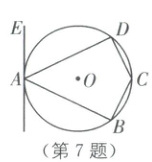
A.$52^{\circ}$
B.$54^{\circ}$
C.$64^{\circ}$
D.$74^{\circ}$
C
).
A.$52^{\circ}$
B.$54^{\circ}$
C.$64^{\circ}$
D.$74^{\circ}$
答案:
7.C [解析]本题考查了切线的性质、圆周角定理、圆内接四边形的性质.
如图,连接AC,

∵∠ADC=90°,
∴AC是⊙O的直径.
∵直线EA与⊙O相切于点A,
∴EA⊥AC,
∴∠CAE=90°.
∵四边形ABCD是圆内接四边形,
∴∠BAD+∠BCD=180°.
∵∠BCD=128°,
∴∠BAD=52°.
∵CD=BC,
∴∠CAD=∠CAB,
∴∠CAD=$\frac{1}{2}$∠BAD=26°,
∴∠DAE=∠CAE−∠CAD=64°.故选C.
中高考趋势 圆的切线垂直于经过切点的半径,经过半径的外端且垂直于这条半径的直线是圆的切线,切线是中高考中比较重要的内容之一,考试必考,在中考中,利用切线时常用辅助线是通过连接切点和圆心,得到直角,判定切线时常常利用“连接圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”直线与圆的公共点”或“过圆心作这条
7.C [解析]本题考查了切线的性质、圆周角定理、圆内接四边形的性质.
如图,连接AC,

∵∠ADC=90°,
∴AC是⊙O的直径.
∵直线EA与⊙O相切于点A,
∴EA⊥AC,
∴∠CAE=90°.
∵四边形ABCD是圆内接四边形,
∴∠BAD+∠BCD=180°.
∵∠BCD=128°,
∴∠BAD=52°.
∵CD=BC,
∴∠CAD=∠CAB,
∴∠CAD=$\frac{1}{2}$∠BAD=26°,
∴∠DAE=∠CAE−∠CAD=64°.故选C.
中高考趋势 圆的切线垂直于经过切点的半径,经过半径的外端且垂直于这条半径的直线是圆的切线,切线是中高考中比较重要的内容之一,考试必考,在中考中,利用切线时常用辅助线是通过连接切点和圆心,得到直角,判定切线时常常利用“连接圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”直线与圆的公共点”或“过圆心作这条
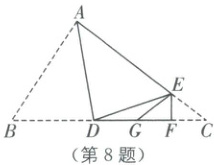
8. 如图,在三角形纸片$ABC$中,$\angle B=57^{\circ}$,$\angle C=38^{\circ}$,将纸片沿着过点$A$的直线折叠,使点$B$落在$AC$边上的点$E$处,折痕$AD$交$BC$于点$D$;再将纸片沿着过点$E$的直线折叠,使点$C$落在$BC$边上的点$G$处,折痕$EF$交$BC$于点$F$.下列结论成立的是(
A.$DG=EG$
B.$GE\perp AE$
C.$\angle DAE=42^{\circ}$
D.$DE=2GF$
A
).
A.$DG=EG$
B.$GE\perp AE$
C.$\angle DAE=42^{\circ}$
D.$DE=2GF$
答案:
8.A[解析]本题考查了三角形的翻折问题、垂直的定义、等腰三角形的判定与性质以及直角三角形中正弦值的求解.
由题可得∠BAC=85°.
∵△ADE是由△ABD翻折得到,
∴∠DAE=∠DAB=42.5°,
∠AED=∠B=57°,故C选项错误,
∴∠ADE=∠ADB=180°−57°−42.5°=80.5°,
∴∠EDG=180°−∠ADE−∠ADB =180°−80.5°×2=19°.
∵△EFG是由△EFC翻折得到,
∴∠EGF=∠C=38°,
∴∠EGD=180°−∠EGF=180°−38°=142°.
在△EGD中,∠DEG=180°−142°−19°=19°.
∵∠EDG=∠DEG=19°,
∴DG=EG.故A选项正确.
∵∠AED+∠DEG=57°+19°=76°,即∠AEG=76°,
∴GE与AE不垂直.
故B选项错误.
过点G作GM⊥DE交DE于点M,如图,

假设DE=2GF.
∵△EFG是由△EFC翻折得到的,
∴∠EFC=∠EFG=90°.
∵DG=EG,
∴△DGE为等腰三角形.
∵GM⊥DE,
∴DM=EM,
∴DE=2EM,
∴GF=EM.
在Rt△EMG中,
sin∠DEG=sin19°=$\frac{MG}{EG}$,
在Rt△EFG中,
sin∠EGF=sin38°=$\frac{EF}{EG}$.
∵sin19°≠sin38°,
∴MG≠EF.
又EM=$\sqrt{EG^{2}-MG^{2}}$≠$\sqrt{EG^{2}-EF^{2}}$,与已知不符,故D选项错误.
综上所述,故选A.
一题多解 判断A选项时.由折叠可知,∠AED=∠B=57°,∠C=∠EGC=38°,
∴∠EDC=∠AED−∠C=57°−38°=19°,
∴∠DEG=∠EGC−∠EDC=38°−19°=19°,
∴∠EDC=∠DEG,
∴DG=EG.
8.A[解析]本题考查了三角形的翻折问题、垂直的定义、等腰三角形的判定与性质以及直角三角形中正弦值的求解.
由题可得∠BAC=85°.
∵△ADE是由△ABD翻折得到,
∴∠DAE=∠DAB=42.5°,
∠AED=∠B=57°,故C选项错误,
∴∠ADE=∠ADB=180°−57°−42.5°=80.5°,
∴∠EDG=180°−∠ADE−∠ADB =180°−80.5°×2=19°.
∵△EFG是由△EFC翻折得到,
∴∠EGF=∠C=38°,
∴∠EGD=180°−∠EGF=180°−38°=142°.
在△EGD中,∠DEG=180°−142°−19°=19°.
∵∠EDG=∠DEG=19°,
∴DG=EG.故A选项正确.
∵∠AED+∠DEG=57°+19°=76°,即∠AEG=76°,
∴GE与AE不垂直.
故B选项错误.
过点G作GM⊥DE交DE于点M,如图,

假设DE=2GF.
∵△EFG是由△EFC翻折得到的,
∴∠EFC=∠EFG=90°.
∵DG=EG,
∴△DGE为等腰三角形.
∵GM⊥DE,
∴DM=EM,
∴DE=2EM,
∴GF=EM.
在Rt△EMG中,
sin∠DEG=sin19°=$\frac{MG}{EG}$,
在Rt△EFG中,
sin∠EGF=sin38°=$\frac{EF}{EG}$.
∵sin19°≠sin38°,
∴MG≠EF.
又EM=$\sqrt{EG^{2}-MG^{2}}$≠$\sqrt{EG^{2}-EF^{2}}$,与已知不符,故D选项错误.
综上所述,故选A.
一题多解 判断A选项时.由折叠可知,∠AED=∠B=57°,∠C=∠EGC=38°,
∴∠EDC=∠AED−∠C=57°−38°=19°,
∴∠DEG=∠EGC−∠EDC=38°−19°=19°,
∴∠EDC=∠DEG,
∴DG=EG.
查看更多完整答案,请扫码查看


