2026年山东省中考试卷精选九年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年山东省中考试卷精选九年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
1.“九达天衢”写成篆体,四个篆体字中可以看作轴对称图形的是(

C
).
答案:
1.C [解析]本题考查了轴对称图形的定义.根据轴对称图形的定义,如果一个图形沿着一条直线对折后,两部分完全重合,那么这个图形就是轴对称图形,据此逐项判断即可.
A.“九”写成篆体后,整体形状不对称,找不到一条直线,使该字沿此直线对折后两部分完全重合,不是轴对称图形;B.“达”写成篆体后,左右两侧形状不一致,找不到一条直线,使该字沿此直线对折后两部分完全重合,不是轴对称图形;C.“天”写成篆体后,能找到一条直线,使该字沿中间竖直方向对折后两部分完全重合,是轴对称图形;D.“衢”写成篆体后,左右结构不对称,找不到一条直线,使该字沿此直线对折后两部分完全重合,不是轴对称图形.故选C.
A.“九”写成篆体后,整体形状不对称,找不到一条直线,使该字沿此直线对折后两部分完全重合,不是轴对称图形;B.“达”写成篆体后,左右两侧形状不一致,找不到一条直线,使该字沿此直线对折后两部分完全重合,不是轴对称图形;C.“天”写成篆体后,能找到一条直线,使该字沿中间竖直方向对折后两部分完全重合,是轴对称图形;D.“衢”写成篆体后,左右结构不对称,找不到一条直线,使该字沿此直线对折后两部分完全重合,不是轴对称图形.故选C.
2.下列实数为无理数的是(
A.$-3$
B.$\sqrt{5}$
C.$\frac{1}{2}$
D.$0.\dot{3}$
B
).A.$-3$
B.$\sqrt{5}$
C.$\frac{1}{2}$
D.$0.\dot{3}$
答案:
2.B [解析]本题考查了无理数的定义.根据无理数的定义判断即可.
A.-3是整数,是有理数不是无理数,故此选项不符合题意;B.$\sqrt{5}$是无理数,故此选项符合题意;C.$\frac{1}{2}$是分数,是有理数不是无理数,故此选项不符合题意;D.0.3是无限循环小数,是有理数不是无理数,故此选项不符合题意.故选B.
知识拓展 无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称,即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.
A.-3是整数,是有理数不是无理数,故此选项不符合题意;B.$\sqrt{5}$是无理数,故此选项符合题意;C.$\frac{1}{2}$是分数,是有理数不是无理数,故此选项不符合题意;D.0.3是无限循环小数,是有理数不是无理数,故此选项不符合题意.故选B.
知识拓展 无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称,即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.
3.某物体的三视图如图所示,与它对应的物体是(

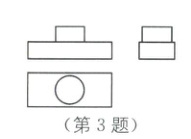
C
).

答案:
3.C [解析]本题考查了由三视图判断几何体.通过分析三视图的形状,尤其是俯视图中的圆,判断物体的组成部分(圆柱和长方体的组合),再结合各视图的特征排除不符合的选项.
由俯视图中有圆,得物体上方侧面应为曲面,排除选项A;由主视图和左视图中下方是长方形,得物体下方应为长方体,排除选项D;由圆柱的直径与长方体的宽度关系,选项B中圆柱直径过宽,不符合视图特征,选项C符合.故选C.
由俯视图中有圆,得物体上方侧面应为曲面,排除选项A;由主视图和左视图中下方是长方形,得物体下方应为长方体,排除选项D;由圆柱的直径与长方体的宽度关系,选项B中圆柱直径过宽,不符合视图特征,选项C符合.故选C.
4.已知 $m$,$n$ 是正整数,且满足 $3^m· 3^n· 3^m=3^n$,则 $m$ 与 $n$ 的关系正确的是(
A.$3m=n$
B.$m^3=n$
C.$m+3=n$
D.$m+1=n$
A
).A.$3m=n$
B.$m^3=n$
C.$m+3=n$
D.$m+1=n$
答案:
4.A [解析]本题考查了同底数幂的乘法运算.
$\because 3^{m}· 3^{n}· 3^{m}=3^{m+n+m}=3^{3m}=3^{n}$,
$\therefore 3m=n$.故选A.
$\because 3^{m}· 3^{n}· 3^{m}=3^{m+n+m}=3^{3m}=3^{n}$,
$\therefore 3m=n$.故选A.
5. 如图,在 $\triangle ABC$ 中,$AB=AC$. 分别以点 $A$ 和点 $B$ 为圆心,大于 $\frac{1}{2}AB$ 的长为半径作弧,两弧交于 $M$,$N$ 两点,作直线 $MN$,与 $AC$ 交于点 $D$,连接 $BD$,若 $\angle A=42°$,则 $\angle CBD$ 的度数为(
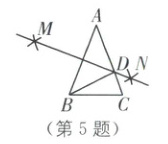
A.$21°$
B.$27°$
C.$30°$
D.$34.5°$
B
).
A.$21°$
B.$27°$
C.$30°$
D.$34.5°$
答案:
5.B [解析]本题考查了等腰三角形的性质和线段垂直平分线的性质.先根据等腰三角形的性质求出$\angle ABC$和$\angle C$的度数,再根据线段垂直平分线的性质得出$AD=BD$,进而求出$\angle ABD$的度数,最后根据$\angle ABC-\angle ABD$求出$\angle CBD$的度数.
$\because AB=AC,\angle A=42^{\circ},\therefore \angle ABC=\angle C=\frac{1}{2}(180^{\circ}-42^{\circ})=69^{\circ}$.由作图可知,MN是线段AB的垂直平分线,
$\therefore AD=BD.\therefore \angle ABD=\angle A=42^{\circ}$,
$\therefore \angle CBD=\angle ABC-\angle ABD=69^{\circ}-42^{\circ}=27^{\circ}$.故选B.
$\because AB=AC,\angle A=42^{\circ},\therefore \angle ABC=\angle C=\frac{1}{2}(180^{\circ}-42^{\circ})=69^{\circ}$.由作图可知,MN是线段AB的垂直平分线,
$\therefore AD=BD.\therefore \angle ABD=\angle A=42^{\circ}$,
$\therefore \angle CBD=\angle ABC-\angle ABD=69^{\circ}-42^{\circ}=27^{\circ}$.故选B.
6. 在平面直角坐标系中,函数 $y=-\frac{1}{|x|}$ 的图象是(

C
).
答案:
6.C [解析]本题考查了反比例函数的图象和性质.化简绝对值,当$x>0$或$x<0$时,分别求出对应函数,确定函数图象所在象限即可.
由题意,得当$x>0$时,$y=-\frac{1}{\vert x\vert }=-\frac{1}{x}<0$,则此时图象分布在第四象限;当$x<0$时,$y=-\frac{1}{\vert x\vert }=-\frac{1}{-x}=\frac{1}{x}<0$,则此时图象分布在第三象限.
故选C.
由题意,得当$x>0$时,$y=-\frac{1}{\vert x\vert }=-\frac{1}{x}<0$,则此时图象分布在第四象限;当$x<0$时,$y=-\frac{1}{\vert x\vert }=-\frac{1}{-x}=\frac{1}{x}<0$,则此时图象分布在第三象限.
故选C.
7.如图,矩形 $OABC$ 的顶点 $O,A,C$ 的坐标分别是 $(0,0),(3,0),(0,2),□ OADE$ 与矩形 $OABC$ 周长相等,$□ OADE$ 的面积是矩形 $OABC$ 面积的一半,则点 $D$ 的坐标为(
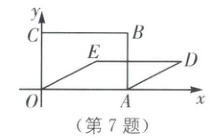
A.$(3+\sqrt{3},1)$
B.$(3+\sqrt{2},\sqrt{2})$
C.$(5,1)$
D.$(3+\sqrt{3},\sqrt{3})$
A
).
A.$(3+\sqrt{3},1)$
B.$(3+\sqrt{2},\sqrt{2})$
C.$(5,1)$
D.$(3+\sqrt{3},\sqrt{3})$
答案:
7.A [解析]本题考查了矩形的性质和面积公式、平行四边形的性质和面积公式及勾股定理.根据题意可得点D的纵坐标是点C纵坐标的一半,$AD=OC=2$,过点D作$DF\bot x$轴,交x轴于点F,用勾股定理求出AF的长即可.
如图,过点D作$DF\bot x$轴,交x轴于点F.

$\because □ OADE$与矩形OABC周长相等,$OA=OA,\therefore AD=OC=2$.
$\because □ OADE$的面积是矩形OABC面积的一半,$OA=OA,\therefore DF=\frac{1}{2}OC=1$.
由勾股定理,得$AF=\sqrt{AD^{2}-DF^{2}}=\sqrt{2^{2}-1^{2}}=\sqrt{3}$,
$\therefore$点D的坐标为$(3+\sqrt{3},1)$.故选A.
7.A [解析]本题考查了矩形的性质和面积公式、平行四边形的性质和面积公式及勾股定理.根据题意可得点D的纵坐标是点C纵坐标的一半,$AD=OC=2$,过点D作$DF\bot x$轴,交x轴于点F,用勾股定理求出AF的长即可.
如图,过点D作$DF\bot x$轴,交x轴于点F.

$\because □ OADE$与矩形OABC周长相等,$OA=OA,\therefore AD=OC=2$.
$\because □ OADE$的面积是矩形OABC面积的一半,$OA=OA,\therefore DF=\frac{1}{2}OC=1$.
由勾股定理,得$AF=\sqrt{AD^{2}-DF^{2}}=\sqrt{2^{2}-1^{2}}=\sqrt{3}$,
$\therefore$点D的坐标为$(3+\sqrt{3},1)$.故选A.
8.如图,从一张半圆形铁片上剪下一个小的半圆形铁片,为了计算剩余部分的面积,在图中作出一条小圆的切线,并使它平行于大圆的直径.设这条切线交大圆于点 $A,B$,量得 $AB$ 的长是 $5 cm$,则剩余部分的面积是(
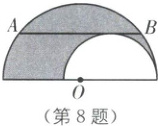
A.$25\pi cm^2$
B.$\frac{25}{2}\pi cm^2$
C.$\frac{25}{4}\pi cm^2$
D.$\frac{25}{8}\pi cm^2$
D
).
A.$25\pi cm^2$
B.$\frac{25}{2}\pi cm^2$
C.$\frac{25}{4}\pi cm^2$
D.$\frac{25}{8}\pi cm^2$
答案:
8.D [解析]本题考查了切线的性质和圆的面积计算.根据切线的性质得到$OC\bot AB$,根据垂径定理求出AC,再根据勾股定理、圆的面积公式计算即可.
如图,平移小圆,使小圆的圆心与点O重合,小圆与AB相切于点C,连接OC,OA.

小圆与AB相切于点C,
$\therefore OC\bot AB,\therefore AC=\frac{1}{2}AB=\frac{5}{2}(cm)$.
在$ Rt\triangle AOC$中,$OA^{2}-OC^{2}=AC^{2}=\frac{25}{4}$,则剩余部分的面积为$\frac{1}{2}× \pi× OA^{2}-\frac{1}{2}× \pi× OC^{2}=\frac{1}{2}× \pi× \frac{25}{4}=\frac{25}{8}\pi( cm^{2})$.故选D.
8.D [解析]本题考查了切线的性质和圆的面积计算.根据切线的性质得到$OC\bot AB$,根据垂径定理求出AC,再根据勾股定理、圆的面积公式计算即可.
如图,平移小圆,使小圆的圆心与点O重合,小圆与AB相切于点C,连接OC,OA.

小圆与AB相切于点C,
$\therefore OC\bot AB,\therefore AC=\frac{1}{2}AB=\frac{5}{2}(cm)$.
在$ Rt\triangle AOC$中,$OA^{2}-OC^{2}=AC^{2}=\frac{25}{4}$,则剩余部分的面积为$\frac{1}{2}× \pi× OA^{2}-\frac{1}{2}× \pi× OC^{2}=\frac{1}{2}× \pi× \frac{25}{4}=\frac{25}{8}\pi( cm^{2})$.故选D.
查看更多完整答案,请扫码查看


