《2026年山东省中考试卷精选九年级数学》

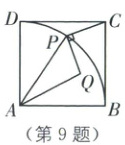
9. 如图，$P$是以正方形$ABCD$的顶点$A$为圆心，$AB$为半径的弧$BD$上的点，连接$AP$，$CP$，将线段$CP$绕点$P$顺时针旋转$90°$后得到线段$PQ$，连接$AQ$.若$AB = 1$，则$\triangle APQ$的最大面积是(C).

A.$\frac{1}{4}$
B.$\frac{2 - \sqrt{3}}{2}$
C.$\frac{\sqrt{2} - 1}{2}$
D.$\frac{\sqrt{2} + 1}{4}$

答案：
9.C　[解析]本题考查了动点问题中的最值问题.
　如图，过点Q作QE⊥AP于点E，过点C作CF⊥AP的延长线于点F，连接AC交弧于点P1，
　　　　　
　则∠QEP=∠CFP=90°.
　又∠QPC=90°,
∴∠EQP+∠EPQ=∠FPC+∠EPQ=90°,
∴∠EQP=∠FPC.
　由旋转，可得PC=PQ，
∴△QPE≌△PCF(AAS),
∴EQ=PF.
∵PF≤PC,
∴EQ≤PC,
∴AP+PF≤AC,
即当点P在P₁时，EQ的值最大，为CP₁的长.
∵四边形ABCD是正方形，
∴AD=AP₁=CD=AB=1,
∴AC=　$\sqrt{AD²+DC²}$=√2,
∴EQ的值最大为CP₁=$\sqrt{2}$−1,
∴△APQ的最大面积是$\frac{1}{2}$×1×($\sqrt{2}$−1)=$\frac{\sqrt{2}−1}{2}$.故选C.
　方法诠释　要计算△APQ的面积，由于AP的长不变，所以需要作出AP 边上的高，由于△PCQ是等腰直角三角形，所以考虑构造一线三等角全等三角形进行线段的转移

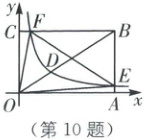
10. 如图，D 为矩形$OABC$(边$OA$，$OC$分别在$x$，$y$轴的正半轴上)对角线$OB$上的点，且$OD = \frac{1}{2} BD$，经过点$D$的反比例函数$y = \frac{k}{x}$的图象分别与$AB$，$BC$相交于点$E$，$F$，连接$OE$，$OF$，$EF$，若$\triangle OBF$的面积是$24$，则$\triangle OEF$的面积为(D).

A.$25$
B.$26$
C.$\frac{79}{3}$
D.$\frac{80}{3}$

答案： 10.D　[解析]本题考查了反比例函数系数k的几何意义.
　由题意，令点A坐标为(a,0)，点C坐标为(0,b)，
　　　　　　　　　　　　　　　　则点B坐标为(a,b).
　　　　　　　　　　　　　　　　因为OD=$\frac{1}{2}$BD,
　　　　　　　　　　　　　　　　所以点D坐标可表示为($\frac{1}{3}$a,$\frac{1}{3}$b).
　　　　　　　　　　　　　　　　因为点D在反比例函数的图象上，
　　　　　　　　　　　　　　　　所以k=$\frac{1}{3}$a·$\frac{1}{3}$b=$\frac{1}{9}$ab,
　　　　　　　　　　　　　　　　则反比例函数表达式为y=$\frac{ab}{9x}$
　　　　　　　　　　　　　　　　又点E，F在反比例函数的图象上，
　　　　　　　　　　　　　　　　所以点F坐标为($\frac{1}{9}$a,b),点E的坐标为(a,$\frac{1}{9}$b)
　　　　　　　　　　　　　　　　所以BF=a−$\frac{1}{9}$a=$\frac{8}{9}$a,BE=
　　　　　　　　　　　　　　　　b−$\frac{1}{9}$b=$\frac{8}{9}$b,
　　　　　　　　　　　　　　　　所以S△OBF=$\frac{1}{2}$×$\frac{8}{9}$a×b=24,
　　　　　　　　　　　　　　　　解得ab=54,
　　　　　　　　　　　　　　　　所以S△OEF=S矩形OABC−S△OCF−S△OEA−S△BEF
　　　　　　　　　　　　　　　　=ab−$\frac{1}{2}$×$\frac{1}{9}$ab−$\frac{1}{2}$×$\frac{8}{9}$ab−$\frac{1}{2}$×$\frac{8}{9}$a×$\frac{8}{9}$b=$\frac{40}{81}$ab=$\frac{80}{3}$.
　　　　　　　　　　　　　　　　故选D.
　　　　　　　　　　　　　　　方法诠释　解答本题需要运用参数的
　　　　　　　　　　　　　　　思想，即设出点B的坐标，然后根据反
　　　　　　　　　　　　　　　比例函数的关系式求出其他关键点的
　　　　　　　　　　　　　　　坐标，然后再利用面积割补法来解决
　　　　　　　　　　　　　　　问题,

11. 因式分解:$2x^2 - 18 =$2(x+3)(x−3).

答案： 11.2(x+3)(x−3)　[解析]本题考查了多项式的因式分解.
　2x²−18=2(x²−9)=2(x+3)(x−3).

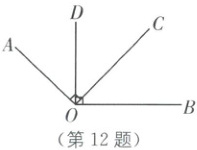
12. 如图，$\angle AOC = \angle BOD = 90°$，$\angle COD = 44°$，则$\angle AOB =$136°.

答案： 12.136°　[解析]本题考查了与两个直角有关的计算.
∵∠AOC=90°,∠COD=44°,
∴∠AOD=∠AOC−∠COD=
　90°−44°=46°.
∵∠BOD=90°,
∴∠AOB=∠AOD+∠BOD=
　46°+90°=136°.

13. 爱好阅读的小胡购买了一本有关数学之美的课外书.如图是他的三个同学猜测该书价格的对话.小胡在听到他们的对话后说:“你们三个都猜错了.”则这本书的价格$x$(元)所在的范围是50＜x＜60.

答案： 13.50＜x＜60　[解析]本题考查了一元一次不等式组的应用.
　根据题意，可得不等式组$\begin{cases} x＞45, \\ x＞50, \\ x＜60, \end{cases}$
　解这个不等式组可得50＜x＜60.

14. 已知矩形$ABCD$，$AB = 4$，$BC = 6$，$P$是边$CD$的中点，$E$是边$AD$上的动点，线段$EF$分别与$BC$，$AP$相交于点$F$，$Q$.若$\angle FQP = 45°$，则$EF$的长为 2$\sqrt{5}$.

答案：
14.2$\sqrt{5}$　[解析]本题考查了与矩形有关的计算.
　如图，在BC上找到一点M,使得BM=
　2,连接AM,PM,则MC=BC−BM=
　6−2=4.
　　　　
　在△ABM和△MCP中，
　$\begin{cases} AB=MC=4, \\ ∠B=∠C=90°, \\ BM=PC=2, \end{cases}$
∴△ABM≌△MCP(SAS),
∴∠BAM=∠CMP,AM=MP,
∴∠AMP=90°,
∴△AMP是等腰直角三角形，
∴∠MAP=45°.
∵∠FQP=45°,
∴∠MAP=∠FQP,
∴AM//EF.又AE//MF,
∴四边形AEFM是平行四边形，
∴EF=AM,
　在Rt△ABM中,由勾股定理,可得AM=
　　√AB²+BM²=　$\sqrt{4²+2²}$=2√5.
　方法诠释　本题直接平移EF，是无法进行求解的，于是构造“K字型”全等三角形是解答本题的关键，然后再证明EF//AM,从而解决问题,

15. 画$1$条直线，最多把$1$张圆形纸片分割成$2$块区域；画$2$条直线，最多把$1$张圆形纸片分割成$4$块区域；画$3$条直线，最多把$1$张圆形纸片分割成$7$块区域；⋯ ，如果要将一张圆形纸片分割成的区域不少于$5 000$块，则至少要画的直线条数是 100.

答案： 15.100　[解析]本题考查了图形变化的规律的探究
　由题意可知，
　画1条直线，最多把1张圆形纸片分割成的区域数为2=1+1;
　画2条直线，最多把1张圆形纸片分割成的区域数为4=1+1+2;
　画3条直线，最多把1张圆形纸片分割成的区域数为7=1+1+2+3;...,
　所以画n条直线，最多把1张圆形纸片分割成的区域数为1+1+2+3+…+n=$\frac{n(n+1)}{2}$+1.
　当n=99时，
　$\frac{n(n+1)}{2}$+1=$\frac{99×100}{2}$+1=4951;当n=100时
　$\frac{n(n+1)}{2}$+1=$\frac{100×101}{2}$+1=5051,所以要将一张圆形纸片分割成的区域不少于5000块，则至少要画的直线条数为100条.
方法诠释　把2,4,7写成2=1+1,4=1+1+2以及7=1+1+2+3是解答本题的关键，也就是要保留原有的数据才可能迅速把区域跟序号进行有机的统一，从而探究出图形变化的规律;

16. (本小题满分 10 分)解方程组$\begin{cases}x - \dfrac{y}{2} = 2, \\2x + 3y = 12.\end{cases}$

答案： 16.[解析]本题考查了解二元一次方程组.掌握消元法来解二元一次方程组是解题的关键.
　解:$\begin{cases} x-\frac{y}{2}=2①, \\ 2x+3y=12②, \end{cases}$
　由①,得x=2+$\frac{y}{2}$③.
　把③代人②,得4+y+3y=12,
　解得y=2.
　把y=2代人③,得x=2+1=3,
∴原方程组的解为$\begin{cases} x=3, \\ y=2. \end{cases}$