2026年山东省中考试卷精选九年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年山东省中考试卷精选九年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第62页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
8. 某射击比赛,甲、乙两名运动员成绩如图所示,根据此统计图,下列结论错误的是(

A.甲队员成绩的中位数是8.5环
B.乙队员成绩的众数是8环
C.乙队员的成绩比甲队员的成绩更稳定
D.乙队员成绩的平均数是8环
A
)。
A.甲队员成绩的中位数是8.5环
B.乙队员成绩的众数是8环
C.乙队员的成绩比甲队员的成绩更稳定
D.乙队员成绩的平均数是8环
答案:
8.A [解析]本题考查了折线统计图.
选项 解析 对错
A 甲队员成绩按从小到大排序为5,6,7,8,8,8,9,9,10,10,中位数为8环,选项说法错误 √
B 由统计图,得乙队员成绩8环出现了6次,出现的次数最多,因此这组成绩的众数是8环,选项说法正确 ×
C 由折线统计图,得乙运动员的10次射击成绩的波动性较小,甲运动员的10次射击成绩的波动性较大,所以乙队员的成绩比甲队员的成绩更稳定,选项说法正确 ×
D 乙队员成绩的平均数是$\frac{1}{10}$×(8×6+9×2+7×2)=8(环),选项说法正确 ×
故选A.
知识拓展 折线统计图:折线图是以折线的上升或下降来表示统计数量增减变化.折线图不但可以表示出数量的多少,而且能够清楚地表示出数量的增减变化情况.
选项 解析 对错
A 甲队员成绩按从小到大排序为5,6,7,8,8,8,9,9,10,10,中位数为8环,选项说法错误 √
B 由统计图,得乙队员成绩8环出现了6次,出现的次数最多,因此这组成绩的众数是8环,选项说法正确 ×
C 由折线统计图,得乙运动员的10次射击成绩的波动性较小,甲运动员的10次射击成绩的波动性较大,所以乙队员的成绩比甲队员的成绩更稳定,选项说法正确 ×
D 乙队员成绩的平均数是$\frac{1}{10}$×(8×6+9×2+7×2)=8(环),选项说法正确 ×
故选A.
知识拓展 折线统计图:折线图是以折线的上升或下降来表示统计数量增减变化.折线图不但可以表示出数量的多少,而且能够清楚地表示出数量的增减变化情况.
9. 如图,在菱形$ABCD$中,$\angle A = 45°$,分别以点$A$和$B$为圆心,以大于$\frac{1}{2}AB$的长为半径作弧,两弧相交于点$M$和$N$,作直线$MN$,交$AD$于点$E$,连接$CE$,若$AB = 2$,则$CE$的长为(
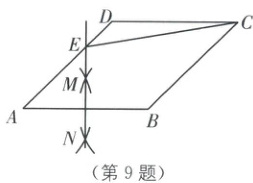
A.$\sqrt{6}$
B.$\sqrt{2} + 1$
C.$\sqrt{3} + 1$
D.$2\sqrt{2}$
A
)。
A.$\sqrt{6}$
B.$\sqrt{2} + 1$
C.$\sqrt{3} + 1$
D.$2\sqrt{2}$
答案:
9.A [解析]本题考查了与菱形有关的作图和相关的计算. 如图,连接BE,设直线MN交AB于点F.

∵四边形ABCD为菱形,
∴BC=AB=2,∠ABC=180°-∠A=135°. 由作图过程可知,直线MN为线段AB的垂直平分线,
∴AE=BE,∠AFE=90°,AF=$\frac{1}{2}$AB=1.
∵∠A=45°,
∴∠ABE=∠A=45°,AE=$\sqrt{2}$AF=$\sqrt{2}$,
∴∠EBC=∠ABC-∠ABE=90°,BE=$\sqrt{2}$. 在Rt△BCE中,由勾股定理,得CE=$\sqrt{BC^{2}+BE^{2}}$=$\sqrt{2^{2}+(\sqrt{2})^{2}}$=$\sqrt{6}$. 故选A.
9.A [解析]本题考查了与菱形有关的作图和相关的计算. 如图,连接BE,设直线MN交AB于点F.

∵四边形ABCD为菱形,
∴BC=AB=2,∠ABC=180°-∠A=135°. 由作图过程可知,直线MN为线段AB的垂直平分线,
∴AE=BE,∠AFE=90°,AF=$\frac{1}{2}$AB=1.
∵∠A=45°,
∴∠ABE=∠A=45°,AE=$\sqrt{2}$AF=$\sqrt{2}$,
∴∠EBC=∠ABC-∠ABE=90°,BE=$\sqrt{2}$. 在Rt△BCE中,由勾股定理,得CE=$\sqrt{BC^{2}+BE^{2}}$=$\sqrt{2^{2}+(\sqrt{2})^{2}}$=$\sqrt{6}$. 故选A.
10. 定义:在平面直角坐标系$xOy$中,横坐标与纵坐标相等的点称为“完美点”。设抛物线$L:y = ax^2 + (a + 1)x - 2a(a \neq 0)$与$y$轴相交于点$M$,将抛物线$L$关于$y$轴对称,且向上平移1个单位后得到抛物线$L'$。若抛物线$L$上的完美点也在抛物线$L'$上,则下列结论:①抛物线$L$上的完美点是$(1,1)$或$(-2,-2)$;②$a$的值是$-\frac{1}{2}$或$-\frac{5}{4}$;③存在某条定直线$l$,与抛物线$L'$交于点$A$,使得$AM$平行于$x$轴。其中正确的是(
A.①②
B.①③
C.②③
D.①②③
D
)。A.①②
B.①③
C.②③
D.①②③
答案:
10.D [解析]本题考查了二次函数图象与系数的关系. 令y=x,则ax^{2}+(a+1)x-2a=x,整理,得ax^{2}+ax-2a=0,即x^{2}+x-2=0,解得x=-2或x=1,
∴抛物线L上的完美点是(1,1)或(-2,-2),故①正确; 将抛物线L关于y轴对称,且向上平移1个单位后得到抛物线L',
∴抛物线L'为y=ax^{2}-(a+1)x-2a+1.
∵抛物线L上的完美点也在抛物线L'上,
∴(1,1)或(-2,-2)也在抛物线L'上,把(1,1)代入y=ax^{2}-(a+1)x-2a+1,得1=a-a-1-2a+1,解得a=-$\frac{1}{2}$. 把(-2,-2)代入y=ax^{2}-(a+1)x-2a+1,得-2=4a+2a+2-2a+1,解得a=-$\frac{5}{4}$,
∴a的值是-$\frac{1}{2}$或-$\frac{5}{4}$,故②正确;
∵抛物线L:y=ax^{2}+(a+1)x-2a(a≠0)与y轴相交于点M,
∴M(0,-2a).
∵抛物线L'上存在点A,使得AM平行于x轴,
∴把y=-2a代入y=ax^{2}-(a+1)x-2a+1,得-2a=ax^{2}-(a+1)x-2a+1,整理,得ax^{2}-(a+1)x+1=0,解得x=1或x=$\frac{1}{a}$,
∴A(1,-2a)或($\frac{1}{a}$,-2a),
∴存在定直线x=1,与抛物线L'交于点A,使得AM平行于x轴,故③正确. 故选D.
∴抛物线L上的完美点是(1,1)或(-2,-2),故①正确; 将抛物线L关于y轴对称,且向上平移1个单位后得到抛物线L',
∴抛物线L'为y=ax^{2}-(a+1)x-2a+1.
∵抛物线L上的完美点也在抛物线L'上,
∴(1,1)或(-2,-2)也在抛物线L'上,把(1,1)代入y=ax^{2}-(a+1)x-2a+1,得1=a-a-1-2a+1,解得a=-$\frac{1}{2}$. 把(-2,-2)代入y=ax^{2}-(a+1)x-2a+1,得-2=4a+2a+2-2a+1,解得a=-$\frac{5}{4}$,
∴a的值是-$\frac{1}{2}$或-$\frac{5}{4}$,故②正确;
∵抛物线L:y=ax^{2}+(a+1)x-2a(a≠0)与y轴相交于点M,
∴M(0,-2a).
∵抛物线L'上存在点A,使得AM平行于x轴,
∴把y=-2a代入y=ax^{2}-(a+1)x-2a+1,得-2a=ax^{2}-(a+1)x-2a+1,整理,得ax^{2}-(a+1)x+1=0,解得x=1或x=$\frac{1}{a}$,
∴A(1,-2a)或($\frac{1}{a}$,-2a),
∴存在定直线x=1,与抛物线L'交于点A,使得AM平行于x轴,故③正确. 故选D.
11. 在一个不透明的盒子中装有4个白球,若干个绿球,它们除颜色不同外,其余均相同。若从中随机摸出一个球是绿球的概率为$\frac{3}{4}$,则绿球的个数为
12
。
答案:
11.12 [解析]本题考查了概率公式的应用. 由题意知,袋中球的总个数为4÷(1-$\frac{3}{4}$)=16,则袋中绿球的个数为16-4=12.
12. 因式分解:$3x^2 - 3 =$
3(x-1)(x+1)
。
答案:
12.3(x-1)(x+1) [解析]本题考查了多项式的因式分解. 原式$=3(x^{2}-1)=3(x-1)(x+1).$
答题规范 因式分解的一般步骤如下:
(1)用提公因式法分解因式;
(2)用公式法分解因式,其中有平方差公式和完全平方公式;
(3)整理结果的形式,单项式因式一般写在前面,相同因式写成幂的形式,同时要注意分解要彻底.
答题规范 因式分解的一般步骤如下:
(1)用提公因式法分解因式;
(2)用公式法分解因式,其中有平方差公式和完全平方公式;
(3)整理结果的形式,单项式因式一般写在前面,相同因式写成幂的形式,同时要注意分解要彻底.
13. 如图,等边三角形$ABC$是$\odot O$的内接三角形,若$\odot O$的半径为4,则阴影部分的面积为
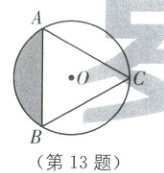
$\frac{16\pi}{3}$-4$\sqrt{3}$
。
答案:
13.$\frac{16\pi}{3}$-4$\sqrt{3}$ [解析]本题考查了与圆有关的阴影部分面积的计算. 如图,连接并且延长AO交BC于点D,连接BO,CO,
∵等边三角形ABC是⊙O的内接三角形,⊙O的半径为4,
∴∠AOB=∠AOC=$\frac{1}{3}$×360°=120°,AO=BO=CO=4,
∴∠BOD=∠COD=180°-120°=60°.
∵BO=CO,OD平分BOC,
∴OD⊥BC,
∴∠ODB=90°,
∴∠OBD=90°-∠BOD=30°,
∴OD=$\frac{1}{2}$BO=2,
∴BD=$\sqrt{BO^{2}-OD^{2}}$=$\sqrt{4^{2}-2^{2}}$=2$\sqrt{3}$,
∴S_{阴影}=S_{扇形AOB}-S_{△AOB}=$\frac{120\pi×4^{2}}{360}$-$\frac{1}{2}$×4×2$\sqrt{3}$=$\frac{16\pi}{3}$-4$\sqrt{3}$.
13.$\frac{16\pi}{3}$-4$\sqrt{3}$ [解析]本题考查了与圆有关的阴影部分面积的计算. 如图,连接并且延长AO交BC于点D,连接BO,CO,
∵等边三角形ABC是⊙O的内接三角形,⊙O的半径为4,
∴∠AOB=∠AOC=$\frac{1}{3}$×360°=120°,AO=BO=CO=4,
∴∠BOD=∠COD=180°-120°=60°.
∵BO=CO,OD平分BOC,
∴OD⊥BC,
∴∠ODB=90°,
∴∠OBD=90°-∠BOD=30°,
∴OD=$\frac{1}{2}$BO=2,
∴BD=$\sqrt{BO^{2}-OD^{2}}$=$\sqrt{4^{2}-2^{2}}$=2$\sqrt{3}$,
∴S_{阴影}=S_{扇形AOB}-S_{△AOB}=$\frac{120\pi×4^{2}}{360}$-$\frac{1}{2}$×4×2$\sqrt{3}$=$\frac{16\pi}{3}$-4$\sqrt{3}$.

14. 虹吸现象描述了液体在两个具有高度差的容器之间,通过充满液体的倒U型管自动流动的过程。如图(1),是利用虹吸现象的原理从甲容器向乙容器注水的示意图,已知甲、乙容器完全相同,开始时甲容器液面高15 cm。设甲容器中的液面高为$y_1$(单位:cm),乙容器中的液面高为$y_2$(单位:cm),小明绘制了$y_1$,$y_2$关于虹吸时间$x$(单位:s)的函数图象,如图(2)所示。当甲容器中的液面比乙容器中的液面低3 cm时,$x$的值为
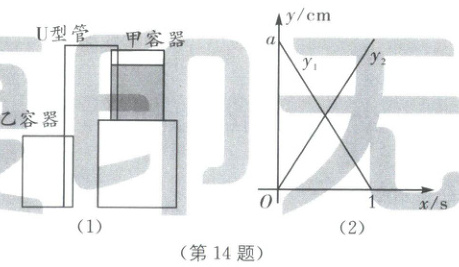
0.6
。
答案:
14.0.6 [解析]本题考查了函数图象的应用. 当x=0时,y_{1}=a,
∵开始时甲容器液面高15cm,
∴a=15. 设y_{1}=kx+b,又当x=1时,y_{1}=0,
∴$\begin{cases}k+b=0,\\b=15,\end{cases}$解得$\begin{cases}k=-15,\\b=15,\end{cases}$
∴y_{1}=-15x+15.
∵甲容器向乙容器倒液体时,y_{1}+y_{2}始终为15,
∴y_{2}=15-y_{1}=15-(-15x+15)=15x,
∴当甲比乙低3cm时,可得y_{1}-y_{2}=-3,
∴(-15x+15)-15x=-3,解得x=0.6.
∵开始时甲容器液面高15cm,
∴a=15. 设y_{1}=kx+b,又当x=1时,y_{1}=0,
∴$\begin{cases}k+b=0,\\b=15,\end{cases}$解得$\begin{cases}k=-15,\\b=15,\end{cases}$
∴y_{1}=-15x+15.
∵甲容器向乙容器倒液体时,y_{1}+y_{2}始终为15,
∴y_{2}=15-y_{1}=15-(-15x+15)=15x,
∴当甲比乙低3cm时,可得y_{1}-y_{2}=-3,
∴(-15x+15)-15x=-3,解得x=0.6.
15. 如图,在$Rt\triangle ABC$中,$\angle ACB = 90°$,$\angle B = 60°$,$BC = 4$,点$M$与点$N$分别在边$AC$与$BC$上,$\angle CNM = 30°$,将$\triangle CMN$沿$MN$翻折得到$\triangle C'MN$,连接$AC'$并将$AC'$绕点$A$逆时针旋转$30°$得到$AE$,连接$CE$,则$CE$的最小值为

6-2$\sqrt{3}$
。
答案:
15.6-2$\sqrt{3}$ [解析]本题考查了动点问题中的最小值问题. 如图,连接CC',作CG⊥AB于点G,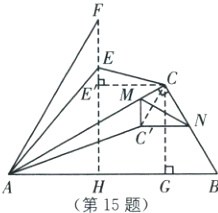
∵∠ACB=90°,∠B=60°,BC=4,
∴AC=$\sqrt{3}$BC=4$\sqrt{3}$,∠BAC=30°,
∴AG=AC·cos∠BAC=4$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=6. 由折叠,得∠MC'N=∠MCN=90°,
∴点C,M,C',N共圆,若四边形对角和等于180°则该四点共圆
∴∠CC'M=∠CNM=30°. 将△ACC'绕点A逆时针旋转30°至△AFE,FE交AB于点H,作CE'⊥EF于点E',
∴∠AFE=∠ACC'=30°,AF=AC=4$\sqrt{3}$,
∴当点E在E'处时,CE最小.
∵∠FAH=∠FAC+∠BAC=60°,∠AFE=30°,
∴∠AHF=90°,
∴AH=AF·cos∠FAH=4$\sqrt{3}$·cos60°,四边形GHE'C是矩形,
∴CE'=GH=AG-AH=6-2$\sqrt{3}$. 即CE的最小值为6-2$\sqrt{3}$.
15.6-2$\sqrt{3}$ [解析]本题考查了动点问题中的最小值问题. 如图,连接CC',作CG⊥AB于点G,

∵∠ACB=90°,∠B=60°,BC=4,
∴AC=$\sqrt{3}$BC=4$\sqrt{3}$,∠BAC=30°,
∴AG=AC·cos∠BAC=4$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=6. 由折叠,得∠MC'N=∠MCN=90°,
∴点C,M,C',N共圆,若四边形对角和等于180°则该四点共圆
∴∠CC'M=∠CNM=30°. 将△ACC'绕点A逆时针旋转30°至△AFE,FE交AB于点H,作CE'⊥EF于点E',
∴∠AFE=∠ACC'=30°,AF=AC=4$\sqrt{3}$,
∴当点E在E'处时,CE最小.
∵∠FAH=∠FAC+∠BAC=60°,∠AFE=30°,
∴∠AHF=90°,
∴AH=AF·cos∠FAH=4$\sqrt{3}$·cos60°,四边形GHE'C是矩形,
∴CE'=GH=AG-AH=6-2$\sqrt{3}$. 即CE的最小值为6-2$\sqrt{3}$.
查看更多完整答案,请扫码查看


