《2026年山东省中考试卷精选九年级数学》

23. (本小题满分 8 分)某文创公司设计了一款黄蓝交汇纪念章,成本价为每个 50 元,以每个不低于成本价且不超过 75 元的价格销售，售价 x(元/个)与每天的销售量 y(个)的对应值表格如下：

(1)求出 y 与 x 的函数表达式,并写出自变量的取值范围;
(2)当售价定为多少元时,每天的利润可达到 6 000 元?

答案： 23.[解析]本题考查了一元二次方程的实际应用和一次函数的实际应用.
(1)根据各数量之间的关系，找到y与x的函数关系式;
(2)找准等量关系，正确列出一元二次方程，解该方程即可.
解:
(1)由题意可知，y是x的一次函数.
设y与x的函数表达式为y=kx十b (k≠0),
把(52,760)，(53,740)分别代入，得$\begin{cases} 760=52k+b,\\ 740=53k+b,\end{cases}$解得$\begin{cases} k=-20,\\ b=1800,\end{cases}$
∴y与x的函数表达式为y=−20x+1800(50≤x≤75).
(2)根据题意，得(x−50)y=6000,
∴(x−50)(−20x+1800)=6000,整理,得x²−140x+4800=0,
解得x₁=60,x₂=80.
∵50≤x≤75,
∴x=60.
故当每个售价定为60元时，每天的利润可达到6000元.

24. (本小题满分 10 分)
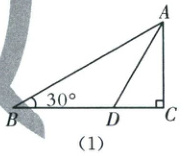
(1)[探索发现]东营市全面落实国家课程方案.某校开设了纸艺课程,三个项目组在折纸活动中发现:在$Rt\triangle ABC$中,$\angle ACB=90^{\circ}$,$\angle ABC=30^{\circ}$,折叠$\triangle ABC$,使 AC 边落在 AB 边上,折痕为 AD,则 BD,CD 与$\angle BAC$的两边 AB,AC 存在着某种关系.如图(1),请你帮助项目组判断$\frac{AB}{AC}$与$\frac{BD}{CD}$的数量关系为$\frac{AB}{AC}$=$\frac{BD}{CD}$.

(2)[猜想验证]项目组猜想:当$\triangle ABC$为任意三角形时,上述数量关系仍然成立.为了验证这一猜想,项目组按照(1)中的方法折叠,AD 为折痕,分别得出了不同的方案,并画出了以下图形.请选择任意一种方案证明.
项目 1 组方案:如图(2),过点 D 作$DE // AC$交 AB 于点 E.
项目 2 组方案:如图(3),过点 C 作$CE // AD$交 BA 的延长线于点 E.
项目 3 组方案:如图(4),过点 C 作$CF \perp AD$交于点 F,过点 B 作$BE \perp AD$交 AD 的延长线于点 E.
(3)[拓展应用]如图(5),在$\triangle ABC$中,AD 平分$\angle BAC$交 BC 于点 D,E 为 BC 延长线上一点,$AE=DE$.
求证:$\frac{BD}{CD}=\frac{DE}{CE}$.

答案：
24.[解析]本题属于相似综合题，主要考查了三角形角平分线的性质、平行线的性质、相似三角形的判定与性质.
(1)解:$\frac{AB}{AC}$=$\frac{BD}{CD}$(或相等)
(2)证明:选择项目1组方案.
如图
(1),
∵DE//AC,

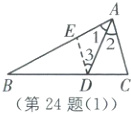
∴∠2=∠3,$\frac{BD}{CD}$=$\frac{BE}{AE}$.
∵∠1=∠2,
∴∠1=∠3,
∴AE=DE,
∴$\frac{BD}{CD}$=$\frac{BE}{DE}$.
∵DE//AC,
∴△BDE∽△BCA,
∴$\frac{BE}{DE}$=$\frac{CA}{AB}$,
选择项目2组方案
如图
(2),
∵CE//AD,

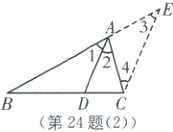
∴∠1=∠3,∠2=∠4.
∵∠1=∠2,
∴∠3=∠4,
∴AE=AC.
∵CE//AD,
∴$\frac{BD}{CD}$=$\frac{AB}{AE}$,即$\frac{AB}{AC}$=$\frac{BD}{CD}$.
选择项目3组方案.
∵CF⊥AD,BE⊥AD,
∴∠AFC=∠CFD=∠BED=90°.
∵∠1=∠2,
∴△ABE∽△ACF,
∴$\frac{AB}{AC}$=$\frac{BE}{CF}$.
∵∠BDE=∠CDF,
∴△BDE∽△CDF,
∴$\frac{BE}{CF}$=$\frac{BD}{CD}$..
∴$\frac{AB}{AC}$=$\frac{BD}{CD}$.
(3)证明:如图
(3).

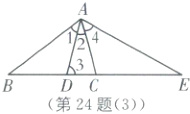
∵AD平分∠BAC,
∴∠1=∠2,$\frac{AB}{AC}$=$\frac{BD}{CD}$.
∵AE=DE,
∴∠3=∠DAE,
∴∠B+∠1=∠2+∠4,
∴∠B=∠4.
又∠AEC=∠BEA,
∴△ABE∽△CAE,
∴$\frac{AB}{AC}$=$\frac{AE}{CE}$,
∴$\frac{BD}{CD}$=$\frac{AE}{CE}$
又AE=DE,
∴$\frac{BD}{CD}$=$\frac{DE}{CE}$.