2026年山东省中考试卷精选九年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年山东省中考试卷精选九年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第32页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
9.如图,在同一平面内放置的$Rt\triangle EFG$和矩形$ABCD$,$EG$与$AB$重合,$FG=3 cm$,$AB=4 cm$,$BC=5 cm$,$Rt\triangle EFG$以$1 cm/s$的速度沿$BC$方向匀速运动,当点 F 与点 C 重合时停止.在运动过程中,$Rt\triangle EFG$与矩形$ABCD$重叠部分的面积$S( cm^2$)与运动时间$t( s$)之间的函数关系图象大致是(
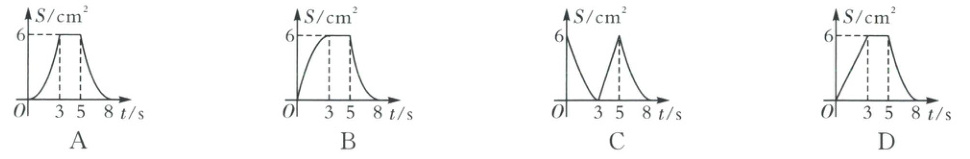
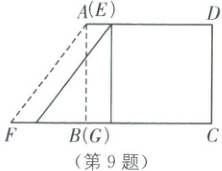
B
).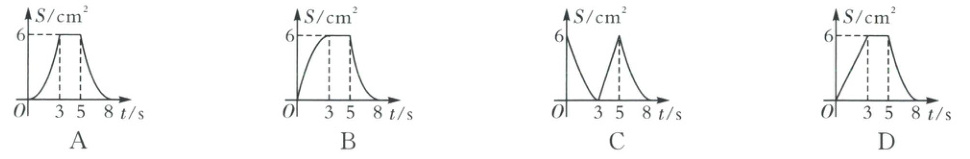

答案:
9.B [解析]本题考查了动点问题、二次函数的图象的性质,分类讨论是解题的关键
如图
(1),当0≤t<3时,设EF与AB 交于点M,此时重叠部分为直角梯形BMEG.
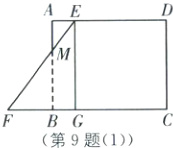
由题意,得BG=tcm,
则BF=(3−t)cm.
∵tanF=$\frac{EG}{FG}$=$\frac{MB}{BF}$=$\frac{4}{3}$,
∴MB=$\frac{4}{3}$(3−t)cm,
∴重叠部分的面积=$\frac{1}{2}$(MB+EG)·BG=$\frac{1}{2}$×[$\frac{4}{3}$(3−t)+4]·t=(−$\frac{2}{3}$t²+4t)cm².
如图
(2),当3≤t<5时,Rt△EFG全部在矩形ABCD内,此时重叠部分为Rt△EFG,
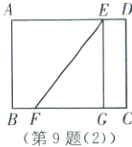
∴此时重叠部分的面积=$\frac{1}{2}$×3×4=6(cm²).
如图
(3),当5≤t≤8时,设EF与CD交于点N,此时重叠部分为Rt△NCF.
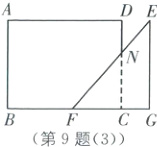
由题意得BG=tcm,则CG=(t−5)cm,CF=(8−t)cm.
同理可得CN=$\frac{4}{3}$(8−t)cm,
∴此时重叠部分的面积=$\frac{1}{2}$×$\frac{4}{3}$(8−t)·(8−t)=$\frac{2}{3}$t²−$\frac{32}{3}$t+$\frac{128}{3}$(cm²).综上所述,选项B符合题意.故选B.
9.B [解析]本题考查了动点问题、二次函数的图象的性质,分类讨论是解题的关键
如图
(1),当0≤t<3时,设EF与AB 交于点M,此时重叠部分为直角梯形BMEG.

由题意,得BG=tcm,
则BF=(3−t)cm.
∵tanF=$\frac{EG}{FG}$=$\frac{MB}{BF}$=$\frac{4}{3}$,
∴MB=$\frac{4}{3}$(3−t)cm,
∴重叠部分的面积=$\frac{1}{2}$(MB+EG)·BG=$\frac{1}{2}$×[$\frac{4}{3}$(3−t)+4]·t=(−$\frac{2}{3}$t²+4t)cm².
如图
(2),当3≤t<5时,Rt△EFG全部在矩形ABCD内,此时重叠部分为Rt△EFG,

∴此时重叠部分的面积=$\frac{1}{2}$×3×4=6(cm²).
如图
(3),当5≤t≤8时,设EF与CD交于点N,此时重叠部分为Rt△NCF.

由题意得BG=tcm,则CG=(t−5)cm,CF=(8−t)cm.
同理可得CN=$\frac{4}{3}$(8−t)cm,
∴此时重叠部分的面积=$\frac{1}{2}$×$\frac{4}{3}$(8−t)·(8−t)=$\frac{2}{3}$t²−$\frac{32}{3}$t+$\frac{128}{3}$(cm²).综上所述,选项B符合题意.故选B.
10.如图,已知四边形$ABCD$是菱形,$\angle ABC=60^{\circ}$,对角线$AC,BD$相交于点 O,过点 D 作$DE \perp BC$交$BC$的延长线于点 E,$F$为$AD$的中点,连接$EF$交$BD$于点 G,连接$OE$交$CD$于点 H,连接$BH$.则下列结论:①$ACEF$为平行四边形;②$\frac{FG}{EG}=\frac{1}{3}$;③$OH^{2}=CH· DH$;④$\tan \angle HBC=\frac{\sqrt{3}}{9}$.其中正确的有(
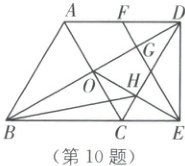
A.①②③
B.①③④
C.②③④
D.①②③④
D
).
A.①②③
B.①③④
C.②③④
D.①②③④
答案:
10.D [解析]本题考查了菱形的性质、相似三角形的判定与性质和锐角三角函数.
∵四边形ABCD是菱形,∠ABC=60°,
∴AD=CD=BC,CD//AB,AD//
BC,
∴∠DCE=60°.
∵∠DEC=90°,
∴CE=CD·cos60°=
$\frac{1}{2}$CD=$\frac{1}{2}$AD.
∵点F是AD的中点,
∴AF=$\frac{1}{2}$AD=CE.
又AD//BC,
∴四边形ACEF为平行四边形.故①正确.
∵CE=$\frac{1}{2}$CD=$\frac{1}{2}$CB,
∴BE=3CE=3AF=3DF.
∵AD//BC,
∴△DFG∽△BEG,
∴$\frac{FG}{EG}$=$\frac{DF}{BE}$=$\frac{1}{3}$.故②正确.
易得CE=CO,
∴∠CEH=∠COH=
$\frac{1}{2}$∠ACB=30°,
∴∠CHE=90°,
∴∠CHO=∠OHD=90°.
又∠DOH=∠DOC−∠COH=60°=
∠OCH,
∴△DHO∽△OHC,
∴$\frac{DH}{OH}$=$\frac{OH}{CH}$,即OH²=CH·DH.
故③正确
如图,过点H作HM⊥BE于点M.
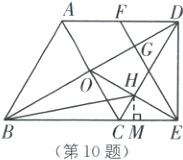
设CM=x,则HM=$\sqrt{3}$x,CH=
2x,
∴CE=2CH=4x,
∴CB=2CE=8x.
在Rt△HBM中,HM=$\sqrt{3}$x,BM=
8x+x=9x,
∴tan∠HBC=$\frac{HM}{BM}$=$\frac{\sqrt{3}x}{9x}$=$\frac{\sqrt{3}}{9}$.故④正确.故选D.
10.D [解析]本题考查了菱形的性质、相似三角形的判定与性质和锐角三角函数.
∵四边形ABCD是菱形,∠ABC=60°,
∴AD=CD=BC,CD//AB,AD//
BC,
∴∠DCE=60°.
∵∠DEC=90°,
∴CE=CD·cos60°=
$\frac{1}{2}$CD=$\frac{1}{2}$AD.
∵点F是AD的中点,
∴AF=$\frac{1}{2}$AD=CE.
又AD//BC,
∴四边形ACEF为平行四边形.故①正确.
∵CE=$\frac{1}{2}$CD=$\frac{1}{2}$CB,
∴BE=3CE=3AF=3DF.
∵AD//BC,
∴△DFG∽△BEG,
∴$\frac{FG}{EG}$=$\frac{DF}{BE}$=$\frac{1}{3}$.故②正确.
易得CE=CO,
∴∠CEH=∠COH=
$\frac{1}{2}$∠ACB=30°,
∴∠CHE=90°,
∴∠CHO=∠OHD=90°.
又∠DOH=∠DOC−∠COH=60°=
∠OCH,
∴△DHO∽△OHC,
∴$\frac{DH}{OH}$=$\frac{OH}{CH}$,即OH²=CH·DH.
故③正确
如图,过点H作HM⊥BE于点M.

设CM=x,则HM=$\sqrt{3}$x,CH=
2x,
∴CE=2CH=4x,
∴CB=2CE=8x.
在Rt△HBM中,HM=$\sqrt{3}$x,BM=
8x+x=9x,
∴tan∠HBC=$\frac{HM}{BM}$=$\frac{\sqrt{3}x}{9x}$=$\frac{\sqrt{3}}{9}$.故④正确.故选D.
11. 中国空间站在太空中的飞行速度约为每小时 27 600 000 米,数据 27 600 000 用科学记数法表示为
2.76×10⁷
.
答案:
11.2.76×10⁷ [解析]本题考查了用科学记数法表示较大的数.
27600000=2.76×10⁷.
27600000=2.76×10⁷.
12.因式分解:$2x^{2}y-4xy^{2}+2y^{3}=$
2y(x−y)²
.
答案:
12.2y(x−y)² [解析]本题考查了因式分解,熟练掌握提公因式法和公式法是解题的关键.
2x²y−4xy²+2y³=2y(x²−2xy+y²)=2y(x−y)².
2x²y−4xy²+2y³=2y(x²−2xy+y²)=2y(x−y)².
13.化简:$(1+\frac{m}{m-1}) ÷ \frac{4m^{2}-1}{m-1}=$
$\frac{1}{2m+1}$
.
答案:
13.$\frac{1}{2m+1}$ [解析]本题考查了分式的混合运算.
原式=$\frac{m−1+m}{m−1}$·$\frac{m−1}{4m²−1}$
=$\frac{2m−1}{m−1}$·$\frac{m−1}{(2m+1)(2m−1)}$
=$\frac{1}{2m+1}$.
原式=$\frac{m−1+m}{m−1}$·$\frac{m−1}{4m²−1}$
=$\frac{2m−1}{m−1}$·$\frac{m−1}{(2m+1)(2m−1)}$
=$\frac{1}{2m+1}$.
14.如图,在平面直角坐标系中,$\odot P$与 x 轴交于点 M,N,与 y 轴相切于点 Q,点 P 的坐标为$(5,-3)$,则点 N 的坐标为
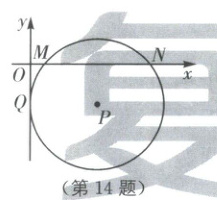
(9,0)
.
答案:
14.(9,0) [解析]本题考查了切线的性质、矩形的判定与性质、垂径定理和勾股定理.
如图,过点P作PH⊥MN于点H,连接PN,PQ,则PQ=PN.
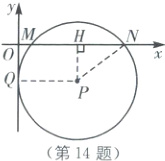
∵OP与y轴相切于点Q,
∴∠OQP=90°,
则四边形OQPH为矩形.
∵点P的坐标为(5,−3),
∴OH=PN=PQ=5,PH=3.
在Rt△PHN中,由勾股定理,得
HN=$\sqrt{PN²−PH²}$=4,
∴ON=OH+HN=9,
∴点N的坐标为(9,0).
14.(9,0) [解析]本题考查了切线的性质、矩形的判定与性质、垂径定理和勾股定理.
如图,过点P作PH⊥MN于点H,连接PN,PQ,则PQ=PN.

∵OP与y轴相切于点Q,
∴∠OQP=90°,
则四边形OQPH为矩形.
∵点P的坐标为(5,−3),
∴OH=PN=PQ=5,PH=3.
在Rt△PHN中,由勾股定理,得
HN=$\sqrt{PN²−PH²}$=4,
∴ON=OH+HN=9,
∴点N的坐标为(9,0).
15.六年级全体数学教师参加“包粽子·迎端午”活动,若每人包 6 个,则比计划多包 9 个;若每人包 4 个,则比计划少包 7 个.求计划包多少个粽子.设计划包 x 个粽子,可列方程为
$\frac{x+9}{6}$=$\frac{x-7}{4}$
.
答案:
15.$\frac{x+9}{6}$=$\frac{x−7}{4}$ [解析]本题考查了一元一次方程的实际应用.解题关键是读懂题意,根据关键描述语,找到等量关系列出方程求解.
根据人数不变,
可列方程为$\frac{x+9}{6}$=$\frac{x−7}{4}$.
根据人数不变,
可列方程为$\frac{x+9}{6}$=$\frac{x−7}{4}$.
16.如图,一次函数$y=3x+3$的图象与坐标轴分别交于点 B,C,反比例函数$y=\frac{k}{x}$的图象经过点 A,$\triangle ABC$是等腰直角三角形,$\angle ACB=90^{\circ}$,$AC=BC$,则 k 的值为
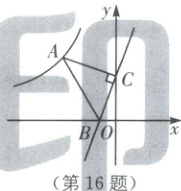
-12
.
答案:
16.−12 [解析]本题考查了反比例函数的图象与性质、全等三角形的判定与性质.
如图,过点A作AD⊥y轴于点D,则∠ADC=∠ACB=∠COB=90°,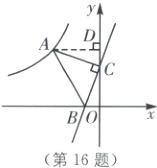
∴∠ACD+∠DAC=90°,∠ACD+∠OCB=90°,
∴∠DAC=∠OCB.
∵AC=BC,
∴△ADC≌△COB(AAS),
∴DC=OB,AD=CO.
在一次函数y=3x+3中,令x=0,得y=3;令y=0,得x=−1,
∴DC=OB=1,AD=CO=3,
∴OD=4,
∴点A的坐标为(−3,4).
∵点A在反比例函数y=$\frac{k}{x}$的图象上,
∴k=−3×4=−12.
16.−12 [解析]本题考查了反比例函数的图象与性质、全等三角形的判定与性质.
如图,过点A作AD⊥y轴于点D,则∠ADC=∠ACB=∠COB=90°,

∴∠ACD+∠DAC=90°,∠ACD+∠OCB=90°,
∴∠DAC=∠OCB.
∵AC=BC,
∴△ADC≌△COB(AAS),
∴DC=OB,AD=CO.
在一次函数y=3x+3中,令x=0,得y=3;令y=0,得x=−1,
∴DC=OB=1,AD=CO=3,
∴OD=4,
∴点A的坐标为(−3,4).
∵点A在反比例函数y=$\frac{k}{x}$的图象上,
∴k=−3×4=−12.
17.如图,四边形$ABCD$是正方形,E 为 CD 上一点,将$\triangle ADE$绕点 A 顺时针旋转$90^{\circ}$至$\triangle ABF$的位置,连接 EF,$AH \perp EF$于点 H,交 BC 于点 G.若$BG=2$,$CG=1$,则 CE 的长为
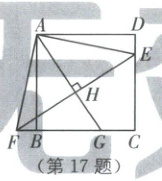
$\frac{12}{5}$
.
答案:
17.$\frac{12}{5}$ [解析]本题考查了全等三角形的判定与性质、正方形的性质、勾股定理.
如图,连接EG.
由旋转的性质可知AE=AF,DE=
BF,且易知F,B,G三点共线
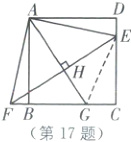
∵AG⊥EF,
∴∠FAG=∠EAG.
∵AG=AG,
∴△FAG≌△EAG(SAS),
∴FG=EG.
∵BG=2,CG=1,
∴BC=3.
∵四边形ABCD是正方形,
∴CD=BC=3,∠C=90°,
∴BF=DE=3−CE,
∴GE=FG=FB+BG=5−CE.在Rt△CEG中,由勾股定理,得GE²=CG²+CE²,
即(5−CE)²=1²+CE²,
解得CE=$\frac{12}{5}$.
17.$\frac{12}{5}$ [解析]本题考查了全等三角形的判定与性质、正方形的性质、勾股定理.
如图,连接EG.
由旋转的性质可知AE=AF,DE=
BF,且易知F,B,G三点共线

∵AG⊥EF,
∴∠FAG=∠EAG.
∵AG=AG,
∴△FAG≌△EAG(SAS),
∴FG=EG.
∵BG=2,CG=1,
∴BC=3.
∵四边形ABCD是正方形,
∴CD=BC=3,∠C=90°,
∴BF=DE=3−CE,
∴GE=FG=FB+BG=5−CE.在Rt△CEG中,由勾股定理,得GE²=CG²+CE²,
即(5−CE)²=1²+CE²,
解得CE=$\frac{12}{5}$.
18.二次函数$y=x^{2}$的图象如图所示,点$B_0$位于坐标原点,点$B_1,B_2,·s,B_n$在 y 轴的正半轴上,点$A_1,A_2,·s,A_n$,点$C_1,C_2,·s,C_n$在二次函数的图象上,四边形$B_0A_1B_1C_1$,四边形$B_1A_2B_2C_2,·s$,四边形$B_{n-1}A_nB_nC_n$都是正方形,则正方形$B_{n-1}A_nB_nC_n$的周长为
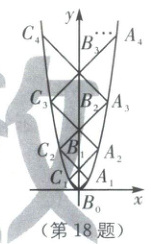
4$\sqrt{2}$n
.
答案:
18.4$\sqrt{2}$n [解析]本题考查了二次函数综合题.利用二次函数图象上点的坐标特征、正方形的性质、等腰直角三角形的性质,推导出正方形的点的坐标是解题的难点.
设点A₁的横坐标为x₁,则由题意可知x₁=x₁²,解得x₁=1(x₁=0已舍去),
∴点A₁的坐标为(1,1),
则正方形B₀A₁B₁C₁的周长为4√2;设点A₂的横坐标为x₂,则由题意可知x₂+2=x₂²,解得x₂=2(负值已舍去),
∴点A₂的坐标为(2,4),则正方形B₁A₂B₂C₂的周长为8√2;设点A₃的横坐标为x₃,则由题意可知x₃+6=x₃²,解得x₃=3(负值已舍去),
∴点A₃的坐标为(3,9),则正方形B₂A₃B₃C₃的周长为12√2,...
∴点An的坐标为(n,n²),则正方形Bₙ₋₁AₙBₙCₙ的周长为4$\sqrt{2}$n.
设点A₁的横坐标为x₁,则由题意可知x₁=x₁²,解得x₁=1(x₁=0已舍去),
∴点A₁的坐标为(1,1),
则正方形B₀A₁B₁C₁的周长为4√2;设点A₂的横坐标为x₂,则由题意可知x₂+2=x₂²,解得x₂=2(负值已舍去),
∴点A₂的坐标为(2,4),则正方形B₁A₂B₂C₂的周长为8√2;设点A₃的横坐标为x₃,则由题意可知x₃+6=x₃²,解得x₃=3(负值已舍去),
∴点A₃的坐标为(3,9),则正方形B₂A₃B₃C₃的周长为12√2,...
∴点An的坐标为(n,n²),则正方形Bₙ₋₁AₙBₙCₙ的周长为4$\sqrt{2}$n.
查看更多完整答案,请扫码查看


