《2026年山东省中考试卷精选九年级数学》

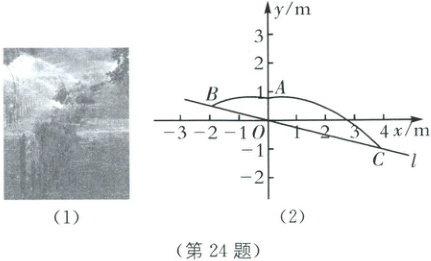
24. (本小题满分 10 分)大泽山葡萄是大家非常喜欢的一种水果，胶东半岛的山坡土壤为大泽山葡萄的生长提供了良好的环境.如图(1)，在山坡上安装一个竖直喷水管向两侧喷水，浇灌葡萄园，喷出的水流呈抛物线状，且两侧水流关于喷水管所在的直线成轴对称，取图(1)的截面，建立如图(2)所示的平面直角坐标系，O 是坐标原点，喷水管为 OA，喷头$A(0,0.8)$，水流落在山坡 l 上的点$B(-2,m)$和点$C(4,-1)$处.
(1) 求山坡 l 和 y 轴右侧抛物线的表达式.
(2) 为了防治虫害，在葡萄树上露出地表 1.1 m 的位置粘贴防虫胶带，请问在坡 OC 段种植的葡萄树，其上粘贴的胶带是否有被水流喷到的风险？

答案： 24.[解析]本题考查了二次函数的应用.
(1)用待定系数法来求函数的表达式;
(2)设水流所在的抛物线到山坡OC 的竖直距离为h,用x表示出h,进而得到h的最大值，与1.1比较即可得出结论
　　解:
(1)设山坡l的表达式为y=kx.
∵过点C(4,−1),
∴−1=4k,解得k=−$\frac{1}{4}$,
∴山坡的表达式为y=−$\frac{1}{4}$x,
∴点B(−2,$\frac{1}{2}$),
∴右侧抛物线上点B的对称点的坐标为(2,$\frac{1}{2}$).
设y轴右侧抛物线表达式为y=
　　ax²+bx+0.8,
∴{41a6a++2b4b++0.08.8==0−.5,1,
　　解得{ab==0−.105.,15,
∴y轴右侧抛物线表达式为y=
　　−0.15x²+0.15x+0.8.
(2)粘贴的胶带没有被水流喷到的风险.理由如下:
　　设水流所在的抛物线到山坡OC的竖直距离为h，
　h=−0.15x²+0.15x+0.8−(−$\frac{1}{4}$
　　=−0.15x²+0.4x+0.8,
∴当x=−$\frac{b}{2a}$=$\frac{4}{3}$时,h最大=$\frac{4ac−b²}{4a}$
　　=$\frac{−0.48−0.16}{−0.6}$=$\frac{16}{15}$＜1.1.
　　故粘贴的胶带没有被水流喷到的风险.

25. (本小题满分 11 分)如图(1)，△ABC 是边长为 8 cm 的等边三角形，Q，D 分别为边 AC，BC 的中点，点 M 从点 D 出发，以$\sqrt{3}$ cm/s 的速度沿 DA 向点 A 运动，过点 M 作$EF // BC$，分别交 AB，AC 于点 E，F；同时，点 P 从点 B 出发，以 4 cm/s 的速度沿 BA 向点 A 运动，设运动时间为$t(s)(0 \leq t \leq 1.5)$.
(1) 当 t 为何值时，点 P 在∠AFE 的平分线上？
(2) 设四边形 PQFE 的面积为$S cm^2$，求 S 与 t 的函数关系式.
(3) 如图(2)，将△AQP 沿 PQ 折叠，A 的对应点为$A'$，是否存在某一时刻 t，使得$A'$落在 EF 上？若存在，求出 t 的值；若不存在，请说明理由.

答案：
25.[解析]本题考查了三角形的综合.
(1)根据等边三角形的性质、勾股定理以及面积法来进行推理和计算;
(2)如图
(2),过点Q作QG⊥AB于点G,过点E作EH⊥BC于点H,根据含30°角的直角三角形的性质和勾股定理以及割补法来进行推理和计算;
(3)根据折叠的性质、相似三角形的判定和性质以及方程的思想来进行推理和计算.
　解:
(1)如图
(1),由题意，得PB=
　4t,DM=$\sqrt{3}$t.
　　　　　
∵△ABC是等边三角形,D是BC 的中点，且边长为8，
∴AD⊥BC,∠B=∠C=∠BAC=
　60°,BD=CD=4,
∴AD=　$\sqrt{8²−4²}$=4$\sqrt{3}$
∴AM=AD−DM=4$\sqrt{3}$-$\sqrt{3}$t.
∵EF/BC,
∴AD⊥EF,∠AEF=
　∠B=60°,∠AFE=∠C=60°,
∴△AEF也是等边三角形，
∴AE=EF.
∵FP平分∠AFE,
∴PF⊥AE.
∵SAE　　$\frac{1}{2}$EF.AM　$\frac{1}{2}$AE.FP,
∴FP=AM=4$\sqrt{3}$$\sqrt{3}$t.
在Rt△APF中,∠PAF=60°,
∴∠AFP=30°,
∴AP=4−t.
∵AB=8,
∴4−t+4t=8,
∴t=$\frac{4}{3}$.
(2)如图
(2),过点Q作QG⊥AB于点G,过点E作EH⊥BC于点H.
　　　
∵Q是AC的中点，
∴AQ=CQ=4.在Rt△AGQ中,∠GAQ=60°,
∴∠AQG=30°,
∴AG　$\frac{1}{2}$AQ=2,GQ=2$\sqrt{3}$.
∵AB=8,BP=4t,
∴AP=8−4t.
在R;△BEH中,∠B=60°,
EH=DM=√3t,
∴∠BEH=30°,
∴BH=t,BE=2t,
∴AE=8−2t=EF,
AE=8−2t=EF,S形POESAICS△AS形BEH割补法是我们计算不规则图
∴形面积常用的方法
=$\frac{1}{2}$×8×4$\sqrt{3}$　$\frac{1}{2}$(8−4)×2√3
$\frac{1}{2}$(8−2t+8)x$\sqrt{3}$t
=√3t²−4√3t+8√3.
故S与I的函数关系式为S
$\sqrt{3}$　　　$\sqrt{3}$+8$\sqrt{3}$.
(3)当　$\frac{5−√5}{2}$时，点A'落在EF上,理由如下:
如图
(3),由折叠的性质,得AQ=AQ=
4,AP=A'P　　8-4t,∠PAQ=
∠PA'Q=60°.
　　　
∵∠PAF=∠AEF+∠EPA'=∠PAQ+∠QAF,∠AEF=∠PAQ=60°,
∴∠QA'F=∠EPA'
∵∠PEA'=∠QFA'=60°,
∴　A'EP　△QFA',
∴$\frac{A'E}{QF}$=$\frac{EP}{A'F}$=$\frac{A'P}{A'Q}$,
$\frac{A'E}{4−2t}$==$\frac{2t}{A'F}$=$\frac{8−4t}{4}$,
∴A'E=2(2−t)²,A'F=$\frac{2t}{2−t}$.
∵EF=A'E+A'F=8−2t,
∴2(2−t)²+$\frac{2t}{2−t}$=8−2t,
∴(2−t)²+$\frac{t}{2−t}$=4−t,
∴(2−t)(t²−3t)+t=0,
∴t=0,t2=$\frac{5+\sqrt{5}}{2}$,t3=$\frac{5−\sqrt{5}}{2}$.
∵0＜t≤1.5,
∴t=$\frac{5−\sqrt{5}}{2}$.
归纳总结　解答本题需要灵活运用相似三角形的判定和性质、等边三角形的性质、折叠的性质、四边形的面积的计算方法，并运用方程的思想来解决问题