《2026年山东省中考试卷精选九年级数学》

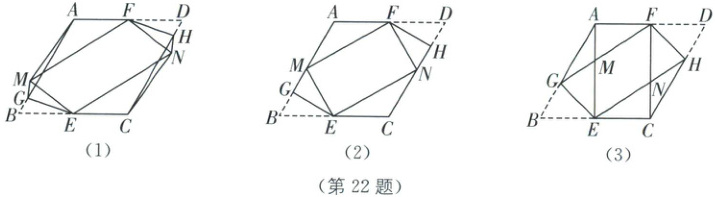
22. (本小题满分 11 分)如图(1),在菱形$ABCD$中,$\angle B=60^{\circ}$,$E$,$F$分别是$BC$,$AD$的中点,点$G$,$H$分别在$AB$,$CD$上,并且$BG=DH$,分别沿$EG$,$FH$折叠菱形$ABCD$,点$B$,$D$的对应点分别为点$M$,$N$,连接$AM$,$CN$,$EN$,$FM$.
(1) 如图(1),请判断线段$AM$,$CN$的位置关系和数量关系,并加以证明;
(2) 如图(2),当点$M$,$N$分别落在$AB$,$CD$上时,请判断四边形$ENFM$的形状,并说明理由;
(3) 如图(3),若点$A$,$M$,$E$恰好在一条直线上时,求$\frac{AG}{BG}$的值.

答案：
22.[解析]本题考查了菱形的性质、全等三角形的性质与判定、平行线的判定、三角函数与等边三角形的性质等知识.
解：
(1)AM=CN，AM//CN.证明如下：
如图
(1)，连接AC.
∵四边形ABCD是菱形，
∴∠BAC=∠DCA.
∵四边形ABCD是菱形，AB=CD.
∵E，F分别是BC，AD的中点，
∴BE=DF.
∵BG=DH，
∴AG=CH.
在△BEG和△DFH中，
$\begin{cases}BG=DH,\\∠B=∠D,\\BE=DF,\end{cases}$
∴△BEG≌△DFH(SAS).
由折叠性质可知△BEG≌△MEG，△DFH≌△NFH，
∴△EMG≌△FNH，
∴∠EGM=∠FHN，MG=NH.
∵∠BGE=∠FHD，
∴∠AGE=∠CHF，
∴∠EGM - ∠AGE=∠FHN - ∠CHF，
∴∠MGA=∠NHC.
在△AMG和△CNH中，
$\begin{cases}MG=NH,\\∠MGA=∠NHC,\\AG=CH,\end{cases}$
∴△AMG≌△CNH(SAS)，
∴AM=CN，∠MAG=∠NCH，
∴∠MAG+∠BAC=∠NCH+∠DCA，
∴∠MAC=∠NCA，
∴AM//CN.

(2)四边形ENFM是矩形.
理由如下：由
(1)可知，△EMG≌△FNH，△AMG≌△CNE，
∴EM=FN，MF=EN，
∴四边形ENFM是平行四边形.
∵∠EMB=∠B=60°，
∴△BME是等边三角形，
∴BM=BE.
∵$BE=\frac{1}{2}BC，$
∴$BM=\frac{1}{2}BC.$
∵$AF=\frac{1}{2}AD，$AB=AD，
∴AM=AF.
∵∠A=120°，
∴∠AMF=30°，
∴∠EMF=90°，
∴四边形ENFM是矩形.
(3)如图
(2)，连接AC.
∵AB=BC，∠B=60°，
∴△ABC是等边三角形.
∵E是BC的中点，
∴$∠BAE=\frac{1}{2}∠BAC=30°.$
又∠GME=∠B=60°，
∴∠MGA=∠MAG，
∴MA=MG.
过点M作MP⊥AB，
∵$\frac{PG}{MG}=cos30°=\frac{\sqrt{3}}{2}，$
∵$PG=\frac{1}{2}AG，$
∴$\frac{\frac{1}{2}AG}{MG}=\frac{\sqrt{3}}{2}，$
∴$\frac{AG}{MG}=\sqrt{3}，$
∵MG=BG，
∴$\frac{AG}{BG}=\sqrt{3}.$

23. (本小题满分 11 分)如图,抛物线$y=x^{2}+bx+c$交$x$轴于$A(-1,0)$,$B(6,0)$两点,交$y$轴于点$C$,连接$BC$,$AC$.
(1) 求抛物线的表达式.
(2) 若$P$是第四象限内抛物线上的一个动点,连接$PB$,$PC$,求$\triangle PBC$面积的最大值,并求出此时点$P$的坐标.
(3) 若$Q$为抛物线对称轴上一点,是否存在点$Q$,使$\triangle BCQ$为直角三角形? 若存在,请直接写出$Q$的坐标;若不存在,请说明理由.

答案：
23.[解析]本题考查了二次函数的图象与性质.
解：
(1)将A(-1,0)，B(6,0)代入$y=x^{2}+bx+c，$
得$\begin{cases}1 - b + c = 0,\\36 + 6b + c = 0,\end{cases}$解得$\begin{cases}b = -5,\\c = -6,\end{cases}$
∴抛物线的表达式为$y=x^{2}-5x - 6.$
(2)如图，过点P作PD⊥x轴于点O，交BC于点E，
∵当x=0时，y=-6，
∴C(0,-6).设直线BC的表达式为$y=kx+b_{1}，$将B(6,0)，C(0,-6)
代入，得$\begin{cases}b_{1} = -6,\\6k + b_{1} = 0,\end{cases}$解得$\begin{cases}k = 1,\\b_{1} = -6,\end{cases}$
∴y=x - 6.设$P(m,m^{2}-5m - 6)，$E(m,m - 6)，
∴$PE=(m - 6)-(m^{2}-5m - 6)=6m - m^{2}，$
∴$S_{△PBC}=S_{△PCE}+S_{△PBE}=\frac{1}{2}PE·OD+\frac{1}{2}PE·BD=\frac{1}{2}PE·OB=\frac{1}{2}(6m - m^{2})×6=-3(m - 3)^{2}+27.$
其中m的取值范围为0＜m＜6
∵-3＜0，
∴当m=3时，S最大=27，当m=3时，$m^{2}-5m - 6=-12，$
∴P(3,-12).

(3)存在.理由如下：
由抛物线的表达式知其对称轴为$x=\frac{5}{2}，$故设点$Q(\frac{5}{2},m)，$由点C，B，Q的坐标，得$BC^{2}=72，$$BQ^{2}=(6-\frac{5}{2})^{2}+m^{2}，$$CQ^{2}=\frac{25}{4}+(m + 6)^{2}，$当BC为斜边时，
则$(6-\frac{5}{2})^{2}+m^{2}+\frac{25}{4}+(m + 6)^{2}=72，$解得$m=\frac{-6±\sqrt{71}}{2}，$即点$Q(\frac{5}{2},\frac{\sqrt{71}-6}{2})$或$(\frac{5}{2},\frac{-\sqrt{71}+6}{2})；$当BQ为斜边时，则$\frac{25}{4}+(m + 6)^{2}+72=(6-\frac{5}{2})^{2}+m^{2}，$解得$m=-\frac{17}{2}，$即点$Q(\frac{5}{2},-\frac{17}{2})；$当CQ为斜边时，则$(6-\frac{5}{2})^{2}+m^{2}+72=\frac{25}{4}+(m + 6)^{2}，$解得$m=\frac{7}{2}，$即点$Q(\frac{5}{2},\frac{7}{2}).$
综上所述，点Q的坐标为$(\frac{5}{2},-\frac{17}{2})$或$(\frac{5}{2},\frac{7}{2})$或$(\frac{5}{2},\frac{\sqrt{71}-6}{2})$或$(\frac{5}{2},\frac{-\sqrt{71}+6}{2}).$