《2026年山东省中考试卷精选九年级数学》

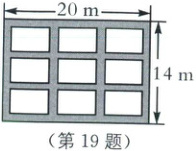
19. (本小题满分 8 分)如图,某校有一块长$20\ {m}$、宽$14\ {m}$的矩形种植园. 为了方便耕作管理,在种植园的四周和内部修建宽度相同的小路(图中阴影部分). 小路把种植园分成面积均为$24\ {m^{2}}$的 9 矩形地块,请你求出小路的宽度.

答案： 19.[解析]本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键.
解：设小路的宽度为$x\ m$，则9块矩形地块可合成长为$(20-4x)\ m$，宽为$(14-4x)\ m$的矩形，
依题意，得$(20-4x)(14-4x)=24×9$，
整理，得$2x^{2}-17x+8=0$，
解得$x_{1}=\frac{1}{2}$，$x_{2}=8$(不符合题意，舍去).故小路的宽度为$\frac{1}{2}\ m$.

20. (本小题满分 9 分)小明同学计划测量小河对面一幢大楼的高度$AB$. 测量方案如图所示：先从自家的阳台点$C$处测得大楼顶部点$B$的仰角$\angle2$的度数,大楼底部点$A$的俯角$\angle1$的度数. 然后在点$C$正下方点$D$处,测得大楼顶部点$B$的仰角$\angle3$的度数. 若$\angle1=45\degree$,$\angle2=52\degree$,$\angle3=65\degree$,$CD=10\ {m}$,求大楼的高度$AB$. (精确到$1\ {m}$,参考数据:$\sin52\degree\approx0.8$,$\cos52\degree\approx0.6$,$\tan52\degree\approx1.3$;$\sin65\degree\approx0.9$,$\cos65\degree\approx0.4$,$\tan65\degree\approx2.1$)

答案：
20.[解析]本题考查了解直角三角形的应用——仰角俯角问题，正确地添加辅助线是解题的关键.
解：如图，过点$C$作$CG\bot AB$于点$G$，过点$D$作$DH\bot AB$于点$H$，

则四边形$CDHG$是矩形，
$\therefore GH=CD=10\ m$，$CG=DH$.
$\because\angle1=45^{\circ}$，$\therefore CG=AG$.
设$CG=AG=DH=x\ m$.
在$ Rt\triangle BCG$中，$\angle2=52^{\circ}$，
$\therefore BG=CG·\tan52^{\circ}\approx1.3x\ m$.
在$ Rt\triangle BDH$中，$\angle3=65^{\circ}$，
$\therefore BH=DH·\tan65^{\circ}\approx2.1x\ m$.
$\therefore GH=BH-BG=2.1x-1.3x=10$，$\therefore x=12.5$，
$\therefore AB=BG+AG=1.3×12.5+12.5\approx29( m)$.
故大楼的高度$AB$约为$29\ m$.
解后反思解直角三角形的应用是中考必考题，问题的特点是将实际生活的物体，利用作辅助线构造直角三角形的方法解题，因为是实际应用问题，数据有时略大，计算要细心，要合理利用题目给定的数据，以勾股定理、三角函数为主要解题方法.解直角三角形的一般过程：①将实际问题抽象为数学问题(画出平面图形，构造出直角三角形转化为解直角三角形问题)；②根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形，得到数学问题的答案，再转化得到实际问题的答案.

21. (本小题满分 9 分)如图,$PA$是$\odotO$的切线,点$A$为切点. 点$B$为$\odotO$上一点,射线$PB$,$AO$交于点$C$,连接$AB$,点$D$在$AB$上,过点$D$作$DF\bot AB$,交$AP$于点$F$,作$DE\bot BP$,垂足为$E$. $AD=BE$,$BD=AF$.
(1)求证：$PB$是$\odotO$的切线；
(2)若$AP=4$,$\sin\angle C=\frac{2}{3}$,求$\odotO$的半径.

答案：
21.[解析]本题是圆的综合题，考查了切线的判定和性质、相似三角形的判定和性质、全等三角形的判定和性质、勾股定理、解直角三角形，正确地添加辅助线是解题的关键.
解：
(1)如图，连接$OB$.

$\because DF\bot AB$，$DE\bot BP$，
$\therefore\angle ADF=\angle DEB=90^{\circ}$.
在$ Rt\triangle BDE$与$ Rt\triangle AFD$中，
$\begin{cases}AD=BE,\\BD=AF,\end{cases}$
$\therefore Rt\triangle BDE\cong Rt\triangle AFD(HL)$，
$\therefore\angle DBE=\angle FAD$.
$\because PA$是$\odot O$的切线，点$A$为切点，
$\therefore\angle CAP=90^{\circ}$，
$\therefore\angle CAB+\angle PAB=90^{\circ}$.
$\because OA=OB$，
$\therefore\angle OAB=\angle OBA$，
$\therefore\angle OBA+\angle ABE=90^{\circ}$，
$\therefore\angle OBE=90^{\circ}$.
$\because PB$是$\odot O$的切线.
(2)$\because\angle CAP=90^{\circ}$，$AP=4$，$\sin C=\frac{AP}{PC}=\frac{2}{3}$，
$\therefore PC=6$，
$\therefore AC=\sqrt{PC^{2}-AP^{2}}=2\sqrt{5}$.
$\because\angle CBO=\angle CAP=90^{\circ}$，$\angle C=\angle C$，
$\therefore\triangle CBO\backsim\triangle CAP$，$\therefore\frac{OB}{AP}=\frac{OC}{PC}$，
$\therefore\frac{OB}{4}=\frac{2\sqrt{5}-OB}{6}$，$\therefore OB=\frac{4\sqrt{5}}{5}$，
即$\odot O$的半径为$\frac{4\sqrt{5}}{5}$.
归纳总结圆的切线垂直于经过切点的半径；经过半径的外端且垂直于这条半径的直线是圆的切线.切线是中考中比较重要的内容之一，利用切线时常用辅助线是连接切点和圆心，得到直角，判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”.