《2026年山东省中考试卷精选九年级数学》

18. (本小题满分 8 分)“春其山中采,香宜竹里煎. 凝成云雾顶,飘出晨露香”描绘了安徽黄山毛峰的独特产地和环境,也表达了其高雅的品质和香气. 徽州某茶叶专卖店的毛峰绿茶进价为每千克 120 元,现在的售价为每千克 150 元,每月可卖出 1500 千克,市场前期调查反映,如调整价格,每千克茶叶售价每涨 1 元,每月少卖出 30 千克,若要求每月销量不少于 1200 千克,试解决下列问题:
(1) 每千克售价最高为多少元?
(2) 实际销售时,发现该茶叶积压较多,为尽快减少库存,经重新调查评估,发现每千克在最高售价的基础上降价销售,每降 1 元,每月销量比最低销量 1200 千克多卖 120 千克,要使利润达到 73920 元,则每千克应降价多少元?

答案： 18.[解析]本题考查了利用一元一次不等式、一元二次方程解决实际问题.
解：
(1)设每千克的售价为x元，依题意得1500 - 30(x - 150)≥1200，解得x≤160.故每千克售价最高为160元.
(2)设每千克应降价y元，则每箱的销售利润为(160 - y - 120)元，每月的销售量为(1200 + 120y)千克，依题意，得(40 - y)(1200 + 120y)=73920，解得$y_{1}=18，$$y_{2}=12.$
∵要尽快减少库存，
∴y=18，故每千克应降价18元.

19. (本小题满分 10 分)无人机在实际生活中的应用越来越广泛. 如图所示,某人利用无人机测量教学楼的高度$BC$,无人机在空中点$P$处,测得点$P$距地面上点$A$处 30 米,点$A$处的俯角为$55^{\circ}$,距楼顶点$C$处 10 米,点$C$处的俯角为$30^{\circ}$,其中点$A$,$B$,$C$,$P$在同一平面内,求该教学楼的高度. (结果保留整数,参考数据:$\sin 55^{\circ} \approx 0.82$,$\cos 55^{\circ} \approx 0.57$,$\tan 55^{\circ} \approx 1.43$)

答案：
19.[解析]本题考查了解直角三角形的实际应用.
解：如图，过点P作PD⊥AB于点D，过点C作CE⊥PD于点E，根据题意可得∠PAB=55°，PA=30米，PC=10米，∠PCE=30°，BC=DE.在Rt△PAD中，$sin55°=\frac{PD}{PA}=\frac{PD}{30}≈0.82，$
∴PD≈24.6米.在Rt△PCE中，$sin30°=\frac{PE}{PC}=\frac{1}{2}，$
∴PE=5米，
∴DE=PD - PE≈20（米），
∴BC=20米，即该教学楼的高度约为20米.

20. (本小题满分 10 分)项目式学习
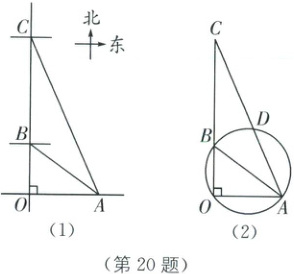
[项目情境]如图(1),$O$,$A$是同一水平线上的两点,过点$O$作$OA$的垂线段$OC$,垂足为$O$,$B$是线段$OC$上的动点. 连接$AB$,以线段$AB$的中点为圆心、$\frac{1}{2}AB$长为半径画圆圆交$AC$于点$D$,不难发现:点$B$越靠近点$C$,线段$CB$,$CD$就越短;反之,点$B$越靠近点$O$,线段$CB$,$CD$就越长.
[问题探究]
(1) 请就图(2)的情形,证明$CD · CA=CB · CO$;
(2) 某一时刻,点$B$运动到如图(1)所示位置,经测量得知此时点$A$在点$B$南偏东$52.9^{\circ}$方向上,在点$C$南偏东$23.2^{\circ}$方向上,点$A$与点$C$的距离为$45 \mathrm{km}$,求此时点$B$与点$C$之间的距离. (精确到$1 \mathrm{km}$,参考数据:$\sin 66.8^{\circ} \approx 0.92$,$\cos 66.8^{\circ} \approx 0.39$,$\tan 37.1^{\circ} \approx 0.76$)

答案：
20.[解析]本题考查了相似三角形、解直角三角形的实际应用.
解：
(1)如图，连接BD，
∵∠C=∠C，∠CDB=∠O，
∴△BCD∽△ACO，
∴$\frac{CD}{CO}=\frac{CB}{CA}，$
∴CD·CA=CB·CO.

(2)在Rt△AOC中，AC=45km，∠OAC =90°-∠OCA=90°-23.2°=66.8°，
∴CO=AC·sin66.8°≈45×0.92=41.4(km)，AO=AC·cos66.8°≈45×0.39=17.55(km).
在Rt△AOB中，∠OAB=90°-∠OBA=90°-52.9°=37.1°，
∴OB=AO·tan37.1°≈17.55×0.76=13.338(km)，
∴BC=CO - OB=41.4 - 13.338≈28(km)，
∴此时点B与点C之间的距离约为28km.