《2026年山东省中考试卷精选九年级数学》

17. (本小题满分 7 分)
(1)计算:$(-3)^{0}-\sqrt[3]{8}+16÷ (-4)$;
(2)解不等式:$x-3(x-2)\geq4$.

答案： 17.[解析]本题主要考查了解一元一次不等式及实数的运算，熟知实数的运算法则及解一元一次不等式的步骤是解题的关键.
解：
(1)原式$=1-2+(-4)=-5$.
(2)$x-3(x-2)\geqslant4$，
$\therefore x-3x+6\geqslant4$，
$\therefore-2x\geqslant-2$，$\therefore x\leqslant1$.
易错警示 不等式的解法往往在解题时不注意移项要改变符号而出错.
解不等式要依据不等式的基本性质：
(1)不等式的两边同时加上或减去同一个数或整式，不等号的方向不变；
(2)不等式的两边同时乘或除以同一个正数，不等号的方向不变；
(3)不等式的两边同时乘或除以同一个负数，不等号的方向改变.

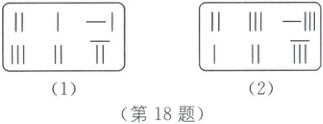
18. (本小题满分 7 分)我国古代很早就开始研究一次方程组,在《九章算术》的“方程”章中，古人用算筹表示一次方程组.例如,如图(1)算筹表示的方程组为$\begin{cases} 2x+y=11,\\3x+2y=7,\end{cases}$图中省略了未知数$x$和$y$,各行从左到右用算筹依次表示未知数$x,y$的系数与相应的常数项.请写出如图(2)算筹所表示的方程组，并求出该方程组的解.

答案： 18.[解析]本题考查了二元一次方程组的应用，找准等量关系，正确列出二元一次方程组是解题的关键.
解：根据题意，得$\begin{cases}2x+3y=13,\\x+2y=8.\end{cases}$
解得$\begin{cases}x=2,\\y=3.\end{cases}$
$\therefore$图
(2)中算筹所表示的方程组为$\begin{cases}2x+3y=13,\\x+2y=8,\end{cases}$
故该方程组的解为$\begin{cases}x=2,\\y=3.\end{cases}$
中考新趋势　近年来，中考数学命题明显加强了对数学文化的考查，而古代数学著作正是其中的核心载体.其“新趋势”可以概括为：从简单的“穿靴戴帽”到深度的“融合应用”，从知识点的考查到思维能力的挖掘.题目直接选取著作中的原题或改编题，其解题思路、方法本身就蕴含着古人的智慧.学生需要理解古文表述，并将其转化为现代数学模型进行求解，不仅考查具体的数学知识(如方程、勾股定理)，更注重挖掘其中的数学思想方法，如模型思想、转化与化归思想、数形结合思想等，考查了学生的综合素养.对于考生而言，这既是挑战也是机遇.挑战在于题目形式更灵活，对综合能力要求更高；机遇在于只要夯实基础、掌握方法、适度拓展，就能在这些体现文化自信和数学魅力的题目上脱颖而出.

19. (本小题满分 8 分)已知$A=x+y$，$B=x^{2}-y^{2}$，$C=\frac{x-y}{x}÷(x-\frac{2xy-y^{2}}{x})$.
(1)若$\frac{A}{B}=\frac{1}{5}$，求$C$的值;
(2)当$y=1$，且$3C$为整数时，求$x$的整数值.

答案： 19.[解析]本题主要考查了分式的化简求值，熟知分式的基本性质是解题的关键.
解：
(1)$\because\frac{A}{B}=\frac{1}{5}$，
$\therefore\frac{x+y}{x^{2}-y^{2}}=\frac{1}{5}$，则$\frac{x+y}{(x-y)(x+y)}=\frac{1}{x-y}=\frac{1}{5}$，
$\therefore C=\frac{x-y}{x}-\frac{x^{2}-2xy+y^{2}}{x}$
$=\frac{x-y}{x}-\frac{(x-y)^{2}}{x}$
$=\frac{1}{x}·(x-y)·[1-(x-y)]$
$=\frac{1}{x}·(x-y)·(1-x+y)=\frac{1}{5}$.
(2)当$y=1$时，$3C=\frac{3}{x-1}$.
$\because3C$为整数，
则$x-1=\pm1$或$\pm3$，
$\therefore$整数$x$的值为$0$或$2$或$-2$或$4$.
$\because x\neq0$且$x\neq1$，
$\therefore$整数$x$的值为$2$或$-2$或$4$.