《2026年山东省中考试卷精选九年级数学》

20. （本小题满分8分）中国集装箱船的制造能力位居全球前列。某校“综合实践”小组想了解大型集装箱船的相关内容，收集得到如下记录表：

（结果精确到0.1米，参考数据：$\sin 7° \approx 0.122$，$\cos 7° \approx 0.993$，$\tan 7° \approx 0.123$，$\sin 4° \approx 0.070$，$\cos 4° \approx 0.998$，$\tan 4° \approx 0.070$，$\sin 20° \approx 0.342$，$\cos 20° \approx 0.940$，$\tan 20° \approx 0.364$）

答案：
20.[解析]本题考查了解直角三角形的应用.
(1)直接利用正切函数来计算；
(2)两次利用正切函数后，进行比较再确定结果. 解：
(1)如图
(1)，由题意，得AD//BC，AB⊥BC，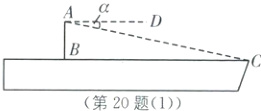
∴∠ACB=∠α=7°. 在Rt△ABC中，AB=BC·tan∠ACB，BC=300米，tan7°≈0.123，
∴AB≈300×0.123=36.9(米)，
∴驾驶塔台AB的高度为36.9米.
(2)该船符合相关安全规定.理由如下： 如图
(2)，延长AB与直线l交于点E，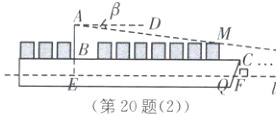
由题意，得AD//l，
∴∠P=∠β=4°，AE=66-15=51(米)，
∴EP=$\frac{AE}{tanP}$=$\frac{51}{tan4°}$≈51÷0.070≈728.6(米). 过点C作CF⊥l于点F，
∴∠QCF=90°-∠CQF=90°-70°=20°，
∴CF=BE=AE-AB=51-36.9=14.1(米). 在Rt△CFQ中，QF=CF·tan∠FCQ=14.1×tan20°≈14.1×0.364≈5.1(米)，
∴PQ=EP-BC+QF=728.6-300+5.1=433.7(米).
∵433.7＜500，
∴该船符合相关安全规定.
归纳总结 解直角三角形的应用，通常会用到“化斜为直”的思想，即如果图形不含直角三角形，此时我们有必要通过作垂线或平行线把非直角三角形的图形转化为直角三角形或是特殊的四边形，然后利用直角三角形中的边角关系来解决问题.