《2026年山东省中考试卷精选九年级数学》

9. 某广场计划用如图(1)所示的$A$,$B$两种瓷砖铺成如图(2)所示的图案. 第一行第一列瓷砖的位置记为$(1,1)$,其右边瓷砖的位置记为$(2,1)$,其上面瓷砖的位置记为$(1,2)$,按照这样的规律,下列说法正确的是(B).


A.$(2024,2025)$位置是$B$种瓷砖
B.$(2025,2025)$位置是$B$种瓷砖
C.$(2026,2026)$位置是$A$种瓷砖
D.$(2025,2026)$位置是$B$种瓷砖

答案： 9.B [解析]本题主要考查规律型——点的坐标，正确找出规律是解题的关键.
A种瓷砖：$(1,2)$，$(1,4)$，$(1,6)$，$·s$，$(2,1)$，$(2,3)$，$(2,5)$，$·s$
B种瓷砖：$(1,1)$，$(1,3)$，$(1,5)$，$·s$，$(2,2)$，$(2,4)$，$(2,6)$，$·s$
由此，可得A种瓷砖的坐标规律为(单数，双数)，(双数，单数)，B种瓷砖的坐标规律为(单数，单数)，(双数，双数)，$(2024,2025)$位置是A种瓷砖，故A不符合题意；
$(2025,2025)$位置是B种瓷砖，故B符合题意；
$(2026,2026)$位置是B种瓷砖，故C不符合题意；
$(2025,2026)$位置是A种瓷砖，故D不符合题意.
故选B.
知识拓展规律问题有数字规律和图形规律.数字规律通常有以下几种：和差规律、乘积规律、指数规律、图形内数字规律、周期规律等；图形规律一般都要先从第一个图形开始确定，一直到第四或第五个图形才能找到正确的规律，再转化为数字规律.

10. 2025 年 5 月,基于“三进制”逻辑的芯片研制成功. 与传统的“二进制”芯片相比,“三进制”逻辑芯片在特定的运算中具有更高的效率.
二进制数的组成数字为 0,1. 十进制数 22 化为二进制数：$22=1×2^{4}+0×2^{3}+1×2^{2}+1×2^{1}+0×2^{0}=10110_{2}$.
传统三进制数的组成数字为 0,1,2. 十进制数 22 化为三进制数：$22=2×3^{2}+1×3^{1}+1×3^{0}=211_{3}$.
将二进制数$1011_{2}$化为三进制数为(A).
A.$102_{3}$
B.$101_{3}$
C.$110_{3}$
D.$12_{3}$

答案： 10.A [解析]本题考查有理数的混合运算，理解题意并列出正确的算式是解题的关键.
将二进制数$1011_{2}$化为十进制数为$1×2^{3}+0×2^{2}+1×2^{1}+1×2^{0}=11$.
$\because11=1×3^{2}+0×3^{1}+2×3^{0}$，
$\therefore$将二进制数$1011_{2}$化为三进制数为$102_{3}$.故选A.

11. 计算：$(\frac{1}{2})^{-1}-\sqrt{8}-(1-\sqrt[3]{2})^{0}=$$1-2\sqrt{2}$.

答案： 11.$1-2\sqrt{2}$ [解析]本题考查实数的运算、负整数指数幂、零指数幂，熟练掌握相关运算法则是解题的关键.
原式$=2-2\sqrt{2}-1=1-2\sqrt{2}$.

12. 若$2x-3y=2$,则$6y-4x+1=$$-3$.

答案： 12.$-3$ [解析]本题考查代数式求值，运用整体代入法代入计算即可求代数式的值.
$\because6y-4x+1=-4x+6y+1$，
$\therefore$当$2x-3y=2$时，原式$=-4x+6y+1=-2(2x-3y)+1=-2×2+1=-3$.

13. 一个不透明的袋子中装有 2 个绿球、1 个白球,每个球除颜色外都相同. 小明同学从袋中随机摸出 1 个球(不放回)后,小华同学再从

袋

中

随机摸出 1 个球. 两人摸到不同颜色球的概率是$\frac{2}{3}$.

答案： 13.$\frac{2}{3}$ [解析]本题考查列表法或画树状图法求概率，熟练掌握列表法与画树状图法求概率是解答本题的关键.
列表如下：
绿 绿 白
绿 （绿，绿） （绿，白）
绿 （绿，绿） （绿，白）
白 （白，绿） （白，绿）
共有6种等可能的结果，其中两人摸到不同颜色球的结果有4种，
$\therefore$两人摸到不同颜色球的概率为$\frac{4}{6}=\frac{2}{3}$.
知识拓展列表法和画树状图法可以不重复不遗漏地列出所有可能的结果，列表法适用于两步完成的事件；画树状图法适用于两步或两步以上完成的事件；解题时要注意此题是放回试验还是不放回试验.用到的知识点为概率=所求情况数与总情况数之比.

14. 如图,小明同学将正方

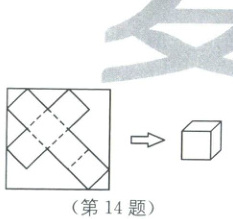
形

硬

纸板沿实线剪开,得到一个立方体的表面展开图. 若正方形硬纸板的边长为 12 cm,则折成立方体的棱长为$\frac{12\sqrt{2}}{5}$cm.

答案：
14.$\frac{12\sqrt{2}}{5}$ [解析]本题考查正方体的展开图以及勾股定理，掌握勾股定理是正确解答的关键.
如图，设$BC=x\ cm$，则$AB=(12-x)\ cm$，$BD=\sqrt{2}x\ cm$，$BE=4\sqrt{2}x\ cm$.

在$ Rt\triangle ABE$中，由勾股定理，得$AE^{2}+AB^{2}=BE^{2}$，
即$(12-x)^{2}+(12-x)^{2}=(4\sqrt{2}x)^{2}$，
解得$x=\frac{12}{5}$或$x=-4$(舍去)，
所以折成正方体的棱长为$\frac{12\sqrt{2}}{5}\ cm$.

15. 如图,点$A$在反比例函数$y=\frac{4}{x}$的图象上,点$B$在反比例函数$y=-\frac{2}{x}$的图象上,连接$OA$,$OB$,$AB$. 若$AO\bot BO$,则$\tan\angle BAO=$$\frac{\sqrt{2}}{2}$.

答案：
15.$\frac{\sqrt{2}}{2}$ [解析]本题考查了相似三角形的判定与性质、反比例函数图象上点的坐标特征，熟练掌握该知识点是解题的关键.
如图，作$BG\bot y$轴，垂足为$G$，作$AH\bot y$轴，垂足为$H$，

$\because$点$A$在反比例函数$y=\frac{4}{x}$的图象上，点$B$在反比例函数$y=\frac{-2}{x}$的图象上，$\therefore S_{\triangle BOG}=1$，$S_{\triangle AOH}=2$.
$\because\angle AOB=90^{\circ}$，
$\therefore\angle AOH+\angle BOG=90^{\circ}$，
由作图可知，$\angle AHO=\angle BGO=90^{\circ}$，
$\therefore\angle AOH+\angle OAH=90^{\circ}$，
$\therefore\angle OAH=\angle BOG$，
$\therefore\triangle OAH\backsim\triangle BOG$，
$\therefore\frac{OB^{2}}{OA^{2}}=\frac{S_{\triangle BOG}}{S_{\triangle AOH}}=\frac{1}{2}$，
$\therefore\tan\angle BAO=\frac{OB}{OA}=\frac{\sqrt{2}}{2}$.
思路引导三角形相似的判定一直是中考考查的热点之一，在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形；依据基本图形对图形进行分解、组合；作辅助线构造相似三角形.判定三角形相似的方法有时可单独使用，有时需要综合运用，无论是单独使用还是综合运用，都要具备应有的条件即可.

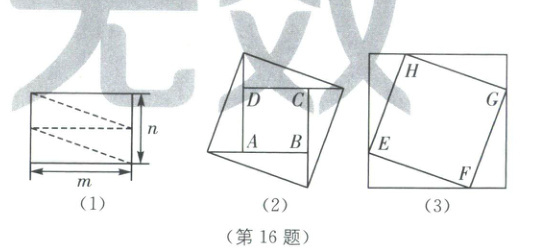
16. 把一张矩形纸片按照如图(1)所示的方式剪成四个全等的直角三角形,四个直角三角形可拼成如图(2)或图(3)所示的正方形. 若矩形纸片的长为$m$,宽为$n$,四边形$EFGH$的面积等于四边形$ABCD$面积的 2 倍, 则$\frac{m}{n}=$$\frac{2+\sqrt{3}}{2}$.

答案： 16.$\frac{2+\sqrt{3}}{2}$ [解析]本题考查图形的拼剪、全等图形、矩形的性质、正方形的性质、勾股定理，解题的关键是学会利用参数构建方程解决问题.
由题意，可得$m^{2}+\frac{n^{2}}{4}=2(m-\frac{1}{2}n)^{2}$，
整理，得$4m^{2}-8mn+n^{2}=0$，
$\therefore m=\frac{2\pm\sqrt{3}}{2}n$.
$\because m＞\frac{1}{2}n$，
$\therefore\frac{m}{n}=\frac{2+\sqrt{3}}{2}$.