《2026年山东省中考试卷精选九年级数学》

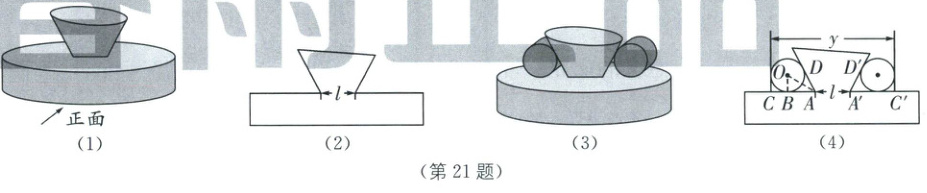
21. (本小题满分 9 分)[问题情境] 2025 年 5 月 29 日“天问二号”成功发射，开启了小行星伴飞取样探测的新篇章. 某校航天兴趣小组受到鼓舞，制作了一个航天器模型，其中某个部件使用 3D 打印完成，如图(1).
[问题提出]部件主视图如图(2)所示，由于$l$的尺寸不易直接测量，需要设计一个可以得到$l$的长度的方案，以检测该部件中$l$的长度是否符合要求.
[方案设计]兴趣小组通过查阅文献，提出了钢柱测量法.
测量工具：游标卡尺、若干个底面圆半径相同的钢柱(圆柱).
操作步骤：如图(3)，将两个钢柱平行放在部件合适位置，使得钢柱与部件紧密贴合. 示意图如图(4)，$\odot O$分别与$AC$，$AD$相切于点$B$，$D$. 用游标卡尺测量出$CC'$的长度$y$.
[问题解决]已知$\angle CAD = \angle C'A'D' = 6 0 ^ { \circ }$，$l$的长度要求是$1.9 cm \sim 2.1 cm$.
(1) 求$\angle BAO$的度数.
(2) 已知钢柱的底面圆半径为$1 cm$，现测得$y = 7.52 cm$. 根据以上信息，通过计算说明该部件$l$的长度是否符合要求(参考数据：$\sqrt { 3 } \approx 1.73$).
[结果反思](3) 本次实践过程借助圆柱将不可测量的长度转化为可测量的长度，能将圆柱换成其他几何体吗？如果能，写出一个；如果不能，说明理由.

答案：
21.[解析]本题考查了切线长定理、解直角三角形的应用.
(1)根据切线长定理求解即可；
(2)解直角三角形求得AB=$\sqrt{3}$，推出AC=1+$\sqrt{3}$，据此求解即可；
(3)能，将圆柱换成正方体.如图，设正方体的棱长为a，用游标卡尺测量出CF的长度y.根据三角函数得到AB=$\frac{\sqrt{3}a}{3}$，进而可得l=y−2(a+$\frac{\sqrt{3}a}{3}$)=y−$\frac{2(3+\sqrt{3})a}{3}$.
解:
(1)
∵⊙O分别与AC，AD相切于点B，D，
∴AB=AD，
∴∠OAB=∠OAD=$\frac{1}{2}$∠CAD=30°.
(2)
∵钢柱的底面圆半径为1cm，
∴BC=OB=1.
∵∠OAB=30°，∠OBA=90°，
∴AB=$\frac{OB}{tan30°}$=$\sqrt{3}$.
∴AC=BC+AB=1+$\sqrt{3}$，
同理A'C'=1+$\sqrt{3}$，
∴l=7.52−2(1+$\sqrt{3}$)≈2.06.
∵1.9＜2.06＜2.1，
∴该部件l的长度符合要求.
(3)能，将圆柱换成正方体(答案不唯一).如图，设正方体的棱长为a，用游标卡尺测量出CF的长度y，
∴BC=BD=a.
∵∠CAD=60°，
∴AB=$\frac{BD}{tan60°}$=$\frac{\sqrt{3}a}{3}$，
∴AC=a+$\frac{\sqrt{3}a}{3}$，
∴l=y−2(a+$\frac{\sqrt{3}a}{3}$)=y−$\frac{2(3+\sqrt{3})a}{3}$.

22. (本小题满分 11 分)已知二次函数$y = x ( x - a ) + ( x - a ) ( x - b ) + x ( x - b )$，其中$a$，$b$为两个不相等的实数.
(1) 当$a = 0$，$b = 3$时，求此函数图象的对称轴.
(2) 当$b = 2a$时，若该函数在$0 \leq x \leq 1$时，$y$随$x$的增大而减小；在$3 \leq x \leq 4$时，$y$随$x$的增大而增大，求$a$的取值范围.
(3) 若点$A ( a , y _ { 1 } )$，$B ( \frac { a + b } { 2 } , y _ { 2 } )$，$C ( b , y _ { 3 } )$均在该函数的图象上，是否存在常数$m$，使得$y _ { 1 } + m y _ { 2 } + y _ { 3 } = 0$？若存在，求出$m$的值；若不存在，说明理由.

答案： 22.[解析]本题考查了二次函数的性质、因式分解的应用.
(1)将a=0，b=3代入y=x(x−a)+(x−a)(x−b)+x(x−b)化简，然后根据二次函数的性质即可解答；
(2)将b=2a代入y=x(x−a)+(x−a)(x−b)+x(x−b)，化简可得y=3x²−6ax+2a²，然后根据二次函数的性质即可解答；
(3)先求出y₁，y₂，y₃，然后代入y₁+my₂+y₃=0进行求解即可.
解:
(1)当a=0，b=3时，二次函数y=x(x−a)+(x−a)(x−b)+x(x−b)可化为y=x(x−0)+(x−0)(x−3)+x(x−3)=3x²−6x，
∴此函数图象的对称轴为直线x=−$\frac{−6}{2×3}$=1.
(2)当b=2a时，二次函数y=x·(x−a)+(x−a)·(x−2a)+x(x−2a)=3x²−6ax+2a²，
∴抛物线的对称轴为直线x=−$\frac{−6a}{2×3}$=a.
∵3＞0，
∴抛物线开口方向向上.
∵在0≤x≤1时，y随x的增大而减小，
∴a≥1.
∵在3≤x≤4时，y随x的增大而增大，
∴a≤3.综上所述，1≤a≤3.
(3)存在.理由如下：
∵点A(a,y₁)，B($\frac{a+b}{2}$,y₂)，C(b,y₃)均在该函数的图象上，
∴y₁=a(a−a)+(a−a)(a−b)+a(a−b)=a²−ab.
∵y=x(x−a)+(x−a)(x−b)+x(x−b)=3x²−2(a+b)x+ab，
∴y₂=3($\frac{a+b}{2}$)²−2(a+b)($\frac{a+b}{2}$)+ab=−$\frac{1}{4}$(a−b)²，y₃=b(b−a)+(b−a)(b−b)+b(b−b)=b²−ab.
∵y₁+my₂+y₃=0，
∴a²−ab+m[−$\frac{1}{4}$(a−b)²]+b²−ab=0，整理得(1−$\frac{1}{4}$m)(a−b)²=0.
∵a,b为两个不相等的实数，
∴a−b≠0，
∴1−$\frac{1}{4}$m=0，解得m=4.