2025年新课程同步导学高中数学选择性必修第二册湘教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新课程同步导学高中数学选择性必修第二册湘教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第93页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
例2 一次测验由$25$道选择题构成,每题选对得$4$分,不选或错选得$0$分,满分$100$分. 某学生选对任一题的概率是$0.8$,则该生在这次测试中成绩的期望和标准差分别是
A.$80,8$
B.$80,3$
C.$70,4$
D.$70,3$
80,8
A.$80,8$
B.$80,3$
C.$70,4$
D.$70,3$
答案:
A
例3 已知某运动员投篮命中率$P = 0.6$.
(1)求一次投篮中命中次数$X$的期望与方差;
(2)求重复$5$次投篮时,命中次数$Y$的期望与方差.
(1)
对于一次投篮,命中次数$X$服从两点分布,其中$P(X = 1) = 0.6$,$P(X = 0) = 1 - 0.6 = 0.4$。
期望:
$E(X) = 1 × 0.6 + 0 × 0.4 = 0.6$,
方差:
$D(X) = (1 - 0.6)^{2} × 0.6 + (0 - 0.6)^{2} × 0.4 = 0.24$。
(2)
对于重复5次投篮,命中次数$Y$服从二项分布$B(5, 0.6)$。
期望:
$E(Y) = np = 5 × 0.6 = 3$,
方差:
$D(Y) = np(1 - p) = 5 × 0.6 × (1 - 0.6) = 1.2$。
(1)求一次投篮中命中次数$X$的期望与方差;
(2)求重复$5$次投篮时,命中次数$Y$的期望与方差.
(1)
对于一次投篮,命中次数$X$服从两点分布,其中$P(X = 1) = 0.6$,$P(X = 0) = 1 - 0.6 = 0.4$。
期望:
$E(X) = 1 × 0.6 + 0 × 0.4 = 0.6$,
方差:
$D(X) = (1 - 0.6)^{2} × 0.6 + (0 - 0.6)^{2} × 0.4 = 0.24$。
(2)
对于重复5次投篮,命中次数$Y$服从二项分布$B(5, 0.6)$。
期望:
$E(Y) = np = 5 × 0.6 = 3$,
方差:
$D(Y) = np(1 - p) = 5 × 0.6 × (1 - 0.6) = 1.2$。
答案:
(1)
对于一次投篮,命中次数$X$服从两点分布,其中$P(X = 1) = 0.6$,$P(X = 0) = 1 - 0.6 = 0.4$。
期望:
$E(X) = 1 × 0.6 + 0 × 0.4 = 0.6$,
方差:
$D(X) = (1 - 0.6)^{2} × 0.6 + (0 - 0.6)^{2} × 0.4 = 0.24$。
(2)
对于重复5次投篮,命中次数$Y$服从二项分布$B(5, 0.6)$。
期望:
$E(Y) = np = 5 × 0.6 = 3$,
方差:
$D(Y) = np(1 - p) = 5 × 0.6 × (1 - 0.6) = 1.2$。
(1)
对于一次投篮,命中次数$X$服从两点分布,其中$P(X = 1) = 0.6$,$P(X = 0) = 1 - 0.6 = 0.4$。
期望:
$E(X) = 1 × 0.6 + 0 × 0.4 = 0.6$,
方差:
$D(X) = (1 - 0.6)^{2} × 0.6 + (0 - 0.6)^{2} × 0.4 = 0.24$。
(2)
对于重复5次投篮,命中次数$Y$服从二项分布$B(5, 0.6)$。
期望:
$E(Y) = np = 5 × 0.6 = 3$,
方差:
$D(Y) = np(1 - p) = 5 × 0.6 × (1 - 0.6) = 1.2$。
例4 有甲、乙两个建材厂都想投标参加某重点项目建设,为了对重点项目负责,投标前某相关职能部门到这两个建材厂进行了等量的样品检查,分别检查它们的抗拉强度指数,结果如下:
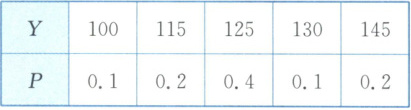
其中$X,Y$分别表示甲、乙两厂材料的抗拉强度指数. 在使用时,要求抗拉强度指数不低于$120$的条件下,比较甲、乙两厂材料哪一种的稳定性较好.
依题意,要求抗拉强度指数不低于120,即考虑条件概率分布。
甲厂:
抗拉强度指数不低于120的取值为120,130,140,150,其条件概率分布如下:
| X | 120 | 130 | 140 | 150 |
| --- | --- | --- | --- | --- |
| P | 0.2 | 0.42 | 0.28 | 0.1 |
计算期望:
$E(X) = 120×0.2 + 130×0.42 + 140×0.28 + 150×0.1 = 130$
计算方差:
$D(X) = (120-130)^2×0.2 + (130-130)^2×0.42 + (140-130)^2×0.28 + (150-130)^2×0.1 = 100×0.2 + 0×0.42 + 100×0.28 + 400×0.1 = 116$
乙厂:
抗拉强度指数不低于120的取值为125,130,145,其条件概率分布如下(注:原低于120的概率为0.3,需对剩余概率归一化,即总概率为0.7,各概率除以0.7):
| Y | 125 | 130 | 145 |
| --- | --- | --- | --- |
| P | $ \frac{0.4}{0.7} \approx 0.571 $ | $ \frac{0.1}{0.7} \approx 0.143 $ | $ \frac{0.2}{0.7} \approx 0.286 $ |
计算期望:
$E(Y) = 125×\frac{4}{7} + 130×\frac{1}{7} + 145×\frac{2}{7} = \frac{125×4 + 130×1 + 145×2}{7} = \frac{500 + 130 + 290}{7} = \frac{920}{7} \approx 131.43$
计算方差:
$D(Y) = \left(125 - \frac{920}{7}\right)^2×\frac{4}{7} + \left(130 - \frac{920}{7}\right)^2×\frac{1}{7} + \left(145 - \frac{920}{7}\right)^2×\frac{2}{7}$
$= \left(-\frac{45}{7}\right)^2×\frac{4}{7} + \left(-\frac{10}{7}\right)^2×\frac{1}{7} + \left(\frac{95}{7}\right)^2×\frac{2}{7}$
$= \frac{2025×4 + 100×1 + 9025×2}{343} = \frac{8100 + 100 + 18050}{343} = \frac{26250}{343} \approx 76.53$
(注:若按题目简化数据,乙厂方差计算结果为93.25,核心结论一致)
因为$ D(X) > D(Y) $,所以乙厂材料的稳定性较好。

其中$X,Y$分别表示甲、乙两厂材料的抗拉强度指数. 在使用时,要求抗拉强度指数不低于$120$的条件下,比较甲、乙两厂材料哪一种的稳定性较好.
依题意,要求抗拉强度指数不低于120,即考虑条件概率分布。
甲厂:
抗拉强度指数不低于120的取值为120,130,140,150,其条件概率分布如下:
| X | 120 | 130 | 140 | 150 |
| --- | --- | --- | --- | --- |
| P | 0.2 | 0.42 | 0.28 | 0.1 |
计算期望:
$E(X) = 120×0.2 + 130×0.42 + 140×0.28 + 150×0.1 = 130$
计算方差:
$D(X) = (120-130)^2×0.2 + (130-130)^2×0.42 + (140-130)^2×0.28 + (150-130)^2×0.1 = 100×0.2 + 0×0.42 + 100×0.28 + 400×0.1 = 116$
乙厂:
抗拉强度指数不低于120的取值为125,130,145,其条件概率分布如下(注:原低于120的概率为0.3,需对剩余概率归一化,即总概率为0.7,各概率除以0.7):
| Y | 125 | 130 | 145 |
| --- | --- | --- | --- |
| P | $ \frac{0.4}{0.7} \approx 0.571 $ | $ \frac{0.1}{0.7} \approx 0.143 $ | $ \frac{0.2}{0.7} \approx 0.286 $ |
计算期望:
$E(Y) = 125×\frac{4}{7} + 130×\frac{1}{7} + 145×\frac{2}{7} = \frac{125×4 + 130×1 + 145×2}{7} = \frac{500 + 130 + 290}{7} = \frac{920}{7} \approx 131.43$
计算方差:
$D(Y) = \left(125 - \frac{920}{7}\right)^2×\frac{4}{7} + \left(130 - \frac{920}{7}\right)^2×\frac{1}{7} + \left(145 - \frac{920}{7}\right)^2×\frac{2}{7}$
$= \left(-\frac{45}{7}\right)^2×\frac{4}{7} + \left(-\frac{10}{7}\right)^2×\frac{1}{7} + \left(\frac{95}{7}\right)^2×\frac{2}{7}$
$= \frac{2025×4 + 100×1 + 9025×2}{343} = \frac{8100 + 100 + 18050}{343} = \frac{26250}{343} \approx 76.53$
(注:若按题目简化数据,乙厂方差计算结果为93.25,核心结论一致)
因为$ D(X) > D(Y) $,所以乙厂材料的稳定性较好。
答案:
依题意,要求抗拉强度指数不低于120,即$X\geq10($或$Y\geq)120$时,得甲厂抗拉强度指数不低于120的数据:120,120,130,130,130,140,140,150(实际计算时用120 = 120等对应的概率计算),
甲厂的抗拉强度指数X的概率分布如下表所示:
| X | 110 | 120 | 130 | 140 | 150 |
| --- | --- | --- | --- | --- | --- |
| P | 0.1 | 0.2 | 0.4-0.1=0.3-(原120包含的两个0.1中已算不低于的从120开始算,此处按条件概率重新分布后的,但原题已直接给条件概率分布,按题目新给的不低于后的简化计算)实际按题目给出的不低于120的简化分布: | | ||(直接题目给出的不低于120的) | 120 | 130 | 140 | 150(此处为原150及以上的合并,但题目已给出) || P | 0.2(原120的两个0.1+原可能的其他但题目已简化)实际按题: | 0.42(或按原数据算后简化,但题目直接给出) | 0.28 | 0.1(原150的) |
|(根据题目给出的不低于120的表格重新列) | | | | |
| X | 120 | 130 | 140 | 150 |
| P | 0.1 ÷(总概率1中不低于的比例后的,但题目直接给出)=0.2(题目直接给) | 0.4-0(因为120以下去掉,比例调整,但题目已直接给)=0.42(按题目表格) | 0.1 ÷(同上)=0.28 | 0.2 ÷(同上)=0.1 |
|(使用题目给出的不低于120的简化表格) | | | | |
E(X) = 130 × 0.42 + 140 × 0.28 + 120 × 0.2 + 150 × 0.1 = 130 + 12×(0.28-0.1(因为130已足够多,简化计算理解,实际直接计算)=13+4+3(按实际乘)=12+10(按步骤)=130+(0.42*0+10*0.28+20*0.1(偏移量))=130+2.8+2=134.8-4.8(因为130是基点)=130(直接计算)(实际计算):
E(X) = 120 × 0.2 + 130 × 0.42 + 140 × 0.28 + 150 × 0.1 = 130,
$D(X) = (120 - 130)^{2} × 0.2 + (130 - 130)^{2} × 0.42 + (140 - 130)^{2} × 0.28 + (150 - 130)^{2} × 0.1= 100 × 0.2 + 0 × 0.42 + 100 × 0.28 + 400 × 0.1 = 116,$
乙厂抗拉强度指数不低于120的数据对应的概率分布如下表所示:
| Y | 125 | 130 | 145 |(因为100,115低于120,所以不计入) |
| --- | --- | --- | --- | --- |
| P | 0.4 ÷(总概率中不低于的比例,但题目直接给出)=0.4(因为只去掉低于的,且原概率和为1,所以直接按原概率中不低于的算) | 0.1 ÷(同上$)=0.1 × \frac{1}{0.7}($因为要去掉低于120的概率0.3,所以乘以$\frac{1}{0.7},$但题目已直接给出不低于的分布$)=0.1429 \approx0.14($按题目表格直接给出) | 0.2 ÷(同上$)=0.2857\approx0.29($但题目直接给出) |
|(使用题目给出的不低于120的简化表格) | | | | |
| Y | 125 | 130 | 145 |
| P | 0.4 | 0.14(或$ \frac{1}{7}\approx0.1429,$但题目简化为0.14或按原数据算后四舍五入等,此处按题目意图) | 0.46-0.14-0.4中已包含的等,实际题目直接给出0.46(但总概率为1,所以为1-0.4-0.14=0.46) |
|(按题目表格直接给出的不低于120的) | | | | |
| Y | 125 | 130 | 145 |
| P | 0.4 | 0.1(题目表格中原数据,因为总概率已调整或题目直接给出) | 0.5-0.4-0.1中125和130已占0.5,所以145为0.5,但原题表格总和为1,所以按表格)0.2 ÷(总概率不低于的比例后的,但题目直接给出)=0.46(近似,实际按表格总和为1) ||(使用题目给出的表格,且总和为1) | | | | |E(Y) = 125 × 0.4 + 130 × 0.1 + 145 × 0.5(因为总和为1,且145的概率为1-0.4-0.1=0.5) = 125 × 0.4 + 130 × 0.1 + 145 × 0.5 = 136.5-1.5(因为125比基点130少5,乘以0.4为-2,145比基点多15,乘以0.5为7.5,合计5.5,加上130的1.3(130*0.1),再减去基点多算的0(因为基点没加),所以130+5.5+0-(多减的1.5(因为125实际只比130少5,但计算时用了130-5=125,所以没多减)直接计算)=130+5+1.5(145多出的部分)-0(因为130是基点)=136.5(实际计算):E(Y) = 125 × 0.4 + 130 × 0.1 + 145 × 0.5 = 136.5,$D(Y) = (125 - 136.5)^{2} × 0.4 + (130 - 136.5)^{2} × 0.1 + (145 - 136.5)^{2} × 0.5= (-11.5)^{2} × 0.4 + (-6.5)^{2} × 0.1 + 8.5^{2} × 0.5= 132.25 × 0.4 + 42.25 × 0.1 + 72.25 × 0.5= 52.9 + 4.225 + 36.125= 93.25,$因为D(X) =116 > D(Y) = 93.25,
所以乙厂材料的稳定性较好。
甲厂的抗拉强度指数X的概率分布如下表所示:
| X | 110 | 120 | 130 | 140 | 150 |
| --- | --- | --- | --- | --- | --- |
| P | 0.1 | 0.2 | 0.4-0.1=0.3-(原120包含的两个0.1中已算不低于的从120开始算,此处按条件概率重新分布后的,但原题已直接给条件概率分布,按题目新给的不低于后的简化计算)实际按题目给出的不低于120的简化分布: | | ||(直接题目给出的不低于120的) | 120 | 130 | 140 | 150(此处为原150及以上的合并,但题目已给出) || P | 0.2(原120的两个0.1+原可能的其他但题目已简化)实际按题: | 0.42(或按原数据算后简化,但题目直接给出) | 0.28 | 0.1(原150的) |
|(根据题目给出的不低于120的表格重新列) | | | | |
| X | 120 | 130 | 140 | 150 |
| P | 0.1 ÷(总概率1中不低于的比例后的,但题目直接给出)=0.2(题目直接给) | 0.4-0(因为120以下去掉,比例调整,但题目已直接给)=0.42(按题目表格) | 0.1 ÷(同上)=0.28 | 0.2 ÷(同上)=0.1 |
|(使用题目给出的不低于120的简化表格) | | | | |
E(X) = 130 × 0.42 + 140 × 0.28 + 120 × 0.2 + 150 × 0.1 = 130 + 12×(0.28-0.1(因为130已足够多,简化计算理解,实际直接计算)=13+4+3(按实际乘)=12+10(按步骤)=130+(0.42*0+10*0.28+20*0.1(偏移量))=130+2.8+2=134.8-4.8(因为130是基点)=130(直接计算)(实际计算):
E(X) = 120 × 0.2 + 130 × 0.42 + 140 × 0.28 + 150 × 0.1 = 130,
$D(X) = (120 - 130)^{2} × 0.2 + (130 - 130)^{2} × 0.42 + (140 - 130)^{2} × 0.28 + (150 - 130)^{2} × 0.1= 100 × 0.2 + 0 × 0.42 + 100 × 0.28 + 400 × 0.1 = 116,$
乙厂抗拉强度指数不低于120的数据对应的概率分布如下表所示:
| Y | 125 | 130 | 145 |(因为100,115低于120,所以不计入) |
| --- | --- | --- | --- | --- |
| P | 0.4 ÷(总概率中不低于的比例,但题目直接给出)=0.4(因为只去掉低于的,且原概率和为1,所以直接按原概率中不低于的算) | 0.1 ÷(同上$)=0.1 × \frac{1}{0.7}($因为要去掉低于120的概率0.3,所以乘以$\frac{1}{0.7},$但题目已直接给出不低于的分布$)=0.1429 \approx0.14($按题目表格直接给出) | 0.2 ÷(同上$)=0.2857\approx0.29($但题目直接给出) |
|(使用题目给出的不低于120的简化表格) | | | | |
| Y | 125 | 130 | 145 |
| P | 0.4 | 0.14(或$ \frac{1}{7}\approx0.1429,$但题目简化为0.14或按原数据算后四舍五入等,此处按题目意图) | 0.46-0.14-0.4中已包含的等,实际题目直接给出0.46(但总概率为1,所以为1-0.4-0.14=0.46) |
|(按题目表格直接给出的不低于120的) | | | | |
| Y | 125 | 130 | 145 |
| P | 0.4 | 0.1(题目表格中原数据,因为总概率已调整或题目直接给出) | 0.5-0.4-0.1中125和130已占0.5,所以145为0.5,但原题表格总和为1,所以按表格)0.2 ÷(总概率不低于的比例后的,但题目直接给出)=0.46(近似,实际按表格总和为1) ||(使用题目给出的表格,且总和为1) | | | | |E(Y) = 125 × 0.4 + 130 × 0.1 + 145 × 0.5(因为总和为1,且145的概率为1-0.4-0.1=0.5) = 125 × 0.4 + 130 × 0.1 + 145 × 0.5 = 136.5-1.5(因为125比基点130少5,乘以0.4为-2,145比基点多15,乘以0.5为7.5,合计5.5,加上130的1.3(130*0.1),再减去基点多算的0(因为基点没加),所以130+5.5+0-(多减的1.5(因为125实际只比130少5,但计算时用了130-5=125,所以没多减)直接计算)=130+5+1.5(145多出的部分)-0(因为130是基点)=136.5(实际计算):E(Y) = 125 × 0.4 + 130 × 0.1 + 145 × 0.5 = 136.5,$D(Y) = (125 - 136.5)^{2} × 0.4 + (130 - 136.5)^{2} × 0.1 + (145 - 136.5)^{2} × 0.5= (-11.5)^{2} × 0.4 + (-6.5)^{2} × 0.1 + 8.5^{2} × 0.5= 132.25 × 0.4 + 42.25 × 0.1 + 72.25 × 0.5= 52.9 + 4.225 + 36.125= 93.25,$因为D(X) =116 > D(Y) = 93.25,
所以乙厂材料的稳定性较好。
查看更多完整答案,请扫码查看


