2025年新课程同步导学高中数学选择性必修第二册湘教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新课程同步导学高中数学选择性必修第二册湘教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第91页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
例4 一个袋子里装有除颜色外均相同的$3$个红球和$2$个黄球,从中同时取出$2$个球,则其中含红球个数$X$的数学期望是
1.2
.
答案:
随机变量$X$的可能取值为$0$,$1$,$2$。
$P(X = 0)=\frac{C_{3}^{0}C_{2}^{2}}{C_{5}^{2}}=\frac{1×1}{10}=\frac{1}{10}$,
$P(X = 1)=\frac{C_{3}^{1}C_{2}^{1}}{C_{5}^{2}}=\frac{3×2}{10}=\frac{6}{10}=\frac{3}{5}$,
$P(X = 2)=\frac{C_{3}^{2}C_{2}^{0}}{C_{5}^{2}}=\frac{3×1}{10}=\frac{3}{10}$。
根据离散型随机变量的数学期望公式$E(X)=\sum_{i}x_{i}P(X = x_{i})$,可得:
$E(X)=0×\frac{1}{10}+1×\frac{3}{5}+2×\frac{3}{10}$
$=0+\frac{3}{5}+\frac{6}{10}$
$=\frac{6 + 6}{10}$
$ = 1.2$
或根据超几何分布的数学期望公式$E(X)=n×\frac{M}{N}$(其中$n$是抽取的样本数,$M$是总体中具有某种特征的单位数,$N$是总体单位数),本题中$n = 2$,$M = 3$,$N = 5$,则$E(X)=2×\frac{3}{5}=1.2$。
故答案为:$1.2$。
$P(X = 0)=\frac{C_{3}^{0}C_{2}^{2}}{C_{5}^{2}}=\frac{1×1}{10}=\frac{1}{10}$,
$P(X = 1)=\frac{C_{3}^{1}C_{2}^{1}}{C_{5}^{2}}=\frac{3×2}{10}=\frac{6}{10}=\frac{3}{5}$,
$P(X = 2)=\frac{C_{3}^{2}C_{2}^{0}}{C_{5}^{2}}=\frac{3×1}{10}=\frac{3}{10}$。
根据离散型随机变量的数学期望公式$E(X)=\sum_{i}x_{i}P(X = x_{i})$,可得:
$E(X)=0×\frac{1}{10}+1×\frac{3}{5}+2×\frac{3}{10}$
$=0+\frac{3}{5}+\frac{6}{10}$
$=\frac{6 + 6}{10}$
$ = 1.2$
或根据超几何分布的数学期望公式$E(X)=n×\frac{M}{N}$(其中$n$是抽取的样本数,$M$是总体中具有某种特征的单位数,$N$是总体单位数),本题中$n = 2$,$M = 3$,$N = 5$,则$E(X)=2×\frac{3}{5}=1.2$。
故答案为:$1.2$。
例5 某城市出租车的起步价为$10$元,行驶路程不超过$4\ km$时不另外收费,若行程超过$4\ km$,则按每超出$1\ km$加收$2$元计费(超出不足$1\ km$的部分按$1\ km$计).从这个城市的民航机场到某宾馆的路程为$15\ km$.某司机经常驾车在机场与该宾馆之间接送旅客,由于行程路线的不同及途中停车时间要转换成行车路程(规定每停车$5\ min$按$1\ km$路程计费).该司机一次接送旅客的行车路程$X$是个随机变量,设出租车费为$Y$.
(1)求出租车费$Y$关于行车路程$X$的关系式,其中行车路程$X$超过$4\ km$;
(2)若随机变量$X$的分布列为
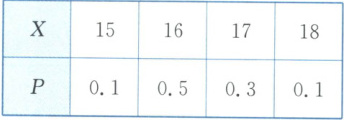
求所收出租车费$Y$的均值;
(3)已知某旅客实付出租车费$38$元,而出租车行驶了$15\ km$,问:出租车在途中因故停车累计最多多少分钟?
(1)
(2)
(3)
(1)求出租车费$Y$关于行车路程$X$的关系式,其中行车路程$X$超过$4\ km$;
(2)若随机变量$X$的分布列为

求所收出租车费$Y$的均值;
(3)已知某旅客实付出租车费$38$元,而出租车行驶了$15\ km$,问:出租车在途中因故停车累计最多多少分钟?
(1)
$Y = 2X + 2$
(2)
$34.8$
(3)
$15$分钟
答案:
(1) $ Y = 2X + 2 $;
(2) $ 34.8 $;
(3) $ 15 $ 分钟。
(1) $ Y = 2X + 2 $;
(2) $ 34.8 $;
(3) $ 15 $ 分钟。
查看更多完整答案,请扫码查看


