《2025年新课程同步导学高中数学选择性必修第二册湘教版》

例1 如图,四边形$ABCD$是边长为$60 cm$的正方形硬纸片.将其切去阴影部分所示的四个全等等腰直角三角形后,再沿虚线折起,使得$ABCD$四个点重合于图中的点$P$,正好形成一个正四棱柱形状的包装盒.已知点$E,F$是$AB$上被切去的等腰直角三角形斜边的两个端点,设$AE = FB = x cm$.

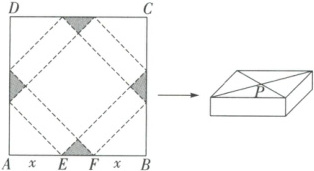
若广告商要求包装盒容积$V(cm^3)$最大,则$x$应取何值？并求出此时包装盒的高与底面边长的比值.
$x=10$；高与底面边长比值为$\frac{1}{4}$。

答案： 由题意，正方形边长60cm，AE=FB=x，EF=60-2x。折起后形成正四棱柱，底面为正方形，边长a=60-2x，高h=x，容积V=a²h=(60-2x)²x，x∈(0,30)。
V(x)=(60-2x)²x=4x³-240x²+3600x，求导得V’(x)=12x²-480x+3600。
令V’(x)=0，即12x²-480x+3600=0，化简x²-40x+300=0，解得x=10或x=30（舍）。
x=10时，V(x)最大。此时底面边长a=60-2×10=40，高h=10，比值h/a=10/40=1/4。
x=10；高与底面边长比值为1/4。

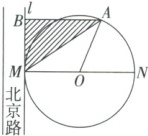
例2 如图,已知圆形花坛$\odot O$的半径为$100 m$,并与北京路一边所在直线$l$相切于点$M$.点$A$为上半圆弧上一点,过点$A$作$l$的垂线,垂足为点$B$.市园林局计划在$\triangle ABM$内进行绿化提质改造.设$\triangle ABM$的面积为$S$(单位：$m^2$),$\angle AON = \theta$.
(1)$ S = 5000\cos\theta(1 + \sin\theta) $，$ \theta \in [0, \frac{\pi}{2}] $将$S$表示为$\theta$的函数；
(2)点$ A $满足$ \angle AON = 30° $，最大面积为$ 3750\sqrt{3} \, m^2 $当面积$S$最大时,试确定点$A$的位置,并求最大面积.

答案：
(1) 以圆心 $ O $ 为坐标原点，$ OM $ 所在直线为 $ y $ 轴（$ OM \perp l $，$ l $ 为切线），设直线 $ l $ 为 $ y = -100 $，则 $ M(0, -100) $，圆半径 $ OA = 100 \, m $。设 $ ON $ 为 $ x $ 轴正方向，$ \angle AON = \theta $，则点 $ A $ 坐标为 $ (100\cos\theta, 100\sin\theta) $（$ \theta \in [0, \frac{\pi}{2}] $，上半圆弧）。过 $ A $ 作 $ l $ 的垂线，垂足 $ B(100\cos\theta, -100) $。
$ \triangle ABM $ 中，$ BM = 100\cos\theta $（底），$ AB = 100\sin\theta - (-100) = 100(1 + \sin\theta) $（高）。
面积 $ S = \frac{1}{2} × BM × AB = \frac{1}{2} × 100\cos\theta × 100(1 + \sin\theta) = 5000\cos\theta(1 + \sin\theta) $。
故 $ S = 5000\cos\theta(1 + \sin\theta) $，$ \theta \in [0, \frac{\pi}{2}] $。
(2) 设 $ f(\theta) = \cos\theta(1 + \sin\theta) $，$ \theta \in [0, \frac{\pi}{2}] $，则 $ S = 5000f(\theta) $。
求导 $ f'(\theta) = -\sin\theta(1 + \sin\theta) + \cos^2\theta = -2\sin^2\theta - \sin\theta + 1 $。
令 $ f'(\theta) = 0 $，即 $ 2\sin^2\theta + \sin\theta - 1 = 0 $，解得 $ \sin\theta = \frac{1}{2} $（$ \sin\theta = -1 $ 舍），则 $ \theta = \frac{\pi}{6} $。
当 $ \theta \in [0, \frac{\pi}{6}) $ 时，$ f'(\theta) ＞ 0 $；$ \theta \in (\frac{\pi}{6}, \frac{\pi}{2}] $ 时，$ f'(\theta) ＜ 0 $，故 $ f(\theta) $ 在 $ \theta = \frac{\pi}{6} $ 取最大值。
$ f(\frac{\pi}{6}) = \cos\frac{\pi}{6}(1 + \sin\frac{\pi}{6}) = \frac{\sqrt{3}}{2} × \frac{3}{2} = \frac{3\sqrt{3}}{4} $。
最大面积 $ S_{max} = 5000 × \frac{3\sqrt{3}}{4} = 3750\sqrt{3} \, m^2 $。
此时点 $ A $ 为上半圆弧上满足 $ \angle AON = \frac{\pi}{6} $（即 $ 30° $）的点。
(1) $ S = 5000\cos\theta(1 + \sin\theta) $，$ \theta \in [0, \frac{\pi}{2}] $；
(2) 点 $ A $ 满足 $ \angle AON = 30° $，最大面积为 $ 3750\sqrt{3} \, m^2 $。