《2025年万唯中考情境题七年级数学上册苏科版》

9. (教材习题第6题改编)如图,$ OC 平分 \angle AOB $, $ OD 平分 \angle BOC $, $ \angle COD = 33^{\circ} $,则$ \angle AOB $的度数为(B)
A.$ 152^{\circ} $
B.$ 132^{\circ} $
C.$ 121^{\circ} $
D.$ 120^{\circ} $

答案： B

10. 在如图所示的正方形网格中,点$ A,B,C,D $均为格点,则$ \angle AOB 和 \angle COD $的大小关系为(A)
A.$ \angle AOB＞\angle COD $
B.$ \angle AOB＜\angle COD $
C.$ \angle AOB = \angle COD $
D.无法比较

答案： A

11. 日常生活情境折纸飞机小琳将一张长方形纸张折成纸飞机.如图是她的操作顺序,则当两侧机翼展开平铺时,两侧机翼与机头的夹角$ \angle ABC $的度数为____.

答案：
45°【解析】如解图,由折叠的性质,得∠HBF=∠HBG=90°,且BD,BE分别平分∠HBF,∠HBG,BA,BC分别平分∠HBD,∠HBE,所以∠ABH=1/2∠HBD=1/2×1/2∠HBF=22.5°.同理可得,∠CBH=22.5°.所以∠ABC=∠ABH+∠CBH=45°.

12. (教材练习第7题改编)如图,点$ E,F 分别在正方形纸片 ABCD 的边 BC,AB $上,将$ \angle B 沿 EF $折叠,使点$ B 落在正方形内部点 G $处,$ EH 为 \angle CEG $内的一条射线.若$ \angle CEG = 3\angle CEH $, $ \angle CEH = 24^{\circ} $,则$ \angle FEH $的度数为____102°.

答案： 102°【解析】因为∠CEG=3∠CEH,∠CEH=24°,所以∠CEG=72°.所以∠BEG=180°−∠CEG=180°−72°=108°.由折叠的性质可知,∠BEF=1/2∠BEG=1/2×108°=54°.所以∠FEH=180°−∠BEF−∠CEH=180°−54°−24°=102°.

13. 如图,已知$ \angle \alpha $, $ \angle \beta $,求作$ \angle AOD = 2\angle \alpha + \beta $. (不写作法,保留作图痕迹)

答案：
解:∠AOD如解图②所示.

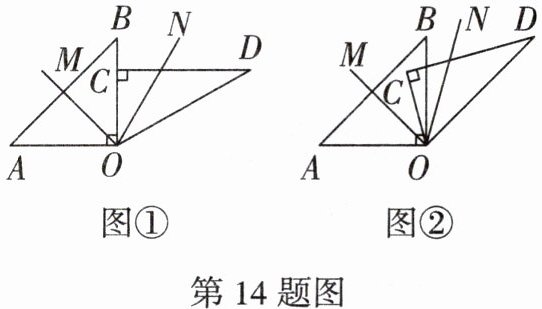
14. 将一副直角三角板按照如图①所示方式放置,三角板$ AOB 与三角板 COD 的顶点 O $重合,已知$ \angle AOB = \angle OCD = 90^{\circ} $,射线$ OM,ON 分别是 \angle AOB,\angle COD $的平分线.
(1)求$ \angle MON $的度数;
(2)如图②,若保持三角尺$ AOB $不动,将三角尺$ COD 绕点 O 以每秒 5^{\circ} $的速度逆时针旋转,旋转一周后运动停止,设运动时间为$ t $ s.
①求当运动时间为$ 3 $ s时,求$ \angle MON $的度数;
②当$ \angle MON = 90^{\circ} $时,求运动时间$ t $的值.

答案：
解:
(1)由题意可得∠AOB=90°,∠COD=60°.因为OM,ON分别是∠AOB,∠COD的平分线，所以∠BOM=1/2∠AOB=45°,∠CON=1/2∠COD =30°.所以∠MON=∠BOM+∠CON=45°+30°=75°;
(2)①由题意可得∠BOC=5°×3=15°,由
(1)可得∠CON=30°,所以∠BON=∠CON−∠BOC=15°.所以∠MON=∠BOM+∠BON=45°+15°=60°;②如解图①，当三角尺COD转过的角度不超过180°时，由题意可得∠BOC=5t°.由
(1)可得∠CON=30°,∠BOM=45°.又因为∠MON=90°,所以∠BOC=∠BOM+∠MON+∠CON=5t°,即45+90+30=5t.解得t=33;如解图②，当三角尺COD转过的角度大于180°时，由题意可得三角尺COD转过的角度=360°−(∠MON−∠BOM−∠CON)=5t°.即360−(90−45−30)=5t,解得t=69.综上所述，当∠MON=90°时，运动时间t的值为33或69.