《2025年万唯中考情境题七年级数学上册苏科版》

1. 可以用 -a 表示的数一定是 (D)
A.负数
B.0 或负数
C.正数或负数
D.以上都不对

答案： D

2. (教材素材改编)若 a,b,c 表示三个有理数,则下列式子中可以表示有理数的乘法分配律的是 (D)
A.$ab = ba$
B.$(a + b)+c = a+(b + c)$
C.$a(bc)= (ab)c$
D.$a(b + c)= ab + ac$

答案： D

3. 非遗展品陈列在文化展览厅,已知一号展厅有 a 件刺绣展品,二号展厅的琉璃展品比一号展厅的刺绣展品少 25 件,则二号展厅的琉璃展品有 (B)
A.$(a + 25)$件
B.$(a - 25)$件
C.$(2a + 25)$件
D.$(25 - a)$件

答案： B

4. (教材习题第 4 题改编)在展览期间,有相关促销活动,已知剪纸书签每张 x 元,9 折出售,传统团扇每把 y 元,7.5 折出售,一位顾客想买 10 张剪纸书签和 20 把传统团扇,预计共需花费(9x+15y)元.

答案： (9x+15y)

5. (教材尝试改编)由于展览期间,客流量较大,文化展览管理部门需要定期对展厅内的展示设备进行检修,已知管理部门有甲、乙两名设备检修员,甲单独检修一台设备需要 a 小时,乙单独检修一台设备需要 b 小时,则两人合作 8 小时可以完成的工作量为$8\left( \frac{1}{a}+\frac{1}{b} \right)$.

答案： $8\left( \frac{1}{a}+\frac{1}{b} \right)$

6. (教材练习第 3 题改编)用字母表示下列运算或数量关系:
(1)减去一个数,等于加上这个数的相反数;
(2)一个数的立方与 2 的差小于 1;
(3)一个数既是 2 的整数倍,又是 3 的整数倍.

答案： 解:
(1)设被减数为a,减数为b. “减去一个数,等于加上这个数的相反数”可以表示为:a-b=a+(-b);
(2)设这个数为x. “一个数的立方与2的差小于1”可以表示为:x^{3}-2＜1;
(3)设n为任意一个不为0的整数. “一个数既是2的整数倍,又是3的整数倍”可以表示为:6n. (答案不唯一)

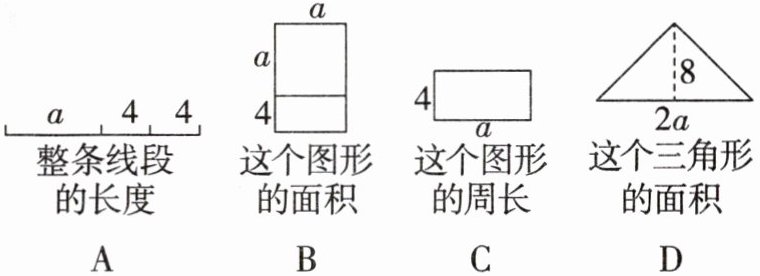
7. 下列选项中,能用 $2a + 8$ 表示的是 (C)

答案： C

8. (代数推理)按一定规律排列的数据:$\frac{9}{5},\frac{16}{12},\frac{25}{21},\frac{36}{32},…$,第 n 个数据为____$\frac{(n+2)^{2}}{n(n+4)}$.

答案： $\frac{(n+2)^{2}}{n(n+4)} 【$解析】因为$ \frac{9}{5}=\frac{(1+2)^{2}}{1×(1+4)},\frac{16}{12}=\frac{(2+2)^{2}}{2×(2+4)},\frac{25}{21}=\frac{(3+2)^{2}}{3×(3+4)},\cdots,$所以第n个数据为$ \frac{(n+2)^{2}}{n(n+4)}.$

9. (教材尝试改编)如图①为佳佳和彤彤制作出的火箭模型(由机身和 3 个机翼组成),图②,图③分别为中间机身(无顶部和底部部分)和机翼的几何示意图,数据如图所示(单位:cm),求制作该模型所用的塑料机身和机翼的材料面积(不计材料厚度).

答案： 解:圆柱的侧面面积为$ 2\pi m×2n=4\pi mn\left( \text{cm}^{2} \right),$梯形的面积为$ \frac{1}{2}m(m+n)\left( \text{cm}^{2} \right),$则制作该模型所用的塑料机身和机翼的材料面积为$ 4\pi mn+3×\frac{1}{2}m(m+n)=\left[ 4\pi mn+\frac{3}{2}m(m+n) \right]\text{cm}^{2}.$