第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
1. 计算2(a + b) + (a - b)的结果是 (
A.3a - b
B.3a + b
C.3a + 2b
D.3a + 3b
B
)A.3a - b
B.3a + b
C.3a + 2b
D.3a + 3b
答案:
B
2. (教材习题第1题改编)下列计算正确的是 (
A.2a + 3b = 5ab
B.x^{4} + x^{3} = x^{7}
C.a^{2} - (b - c) = a^{2} - b - c
D.x^{4} + 2(x^{4} - x^{2}) = 3x^{4} - 2x^{2}
D
)A.2a + 3b = 5ab
B.x^{4} + x^{3} = x^{7}
C.a^{2} - (b - c) = a^{2} - b - c
D.x^{4} + 2(x^{4} - x^{2}) = 3x^{4} - 2x^{2}
答案:
D
3. (教材练习第2题改编)老师在黑板上写了一个正确的演算过程,随后用手捂住了一个多项式:+2xy - 3y = x^{2} + xy,则被手捂住的多项式是 (
A.x^{2} - xy
B.x^{2} - xy + 3y
C.x^{2} - xy - 3y
D.x^{2} + 3xy - 3y
B
)A.x^{2} - xy
B.x^{2} - xy + 3y
C.x^{2} - xy - 3y
D.x^{2} + 3xy - 3y
答案:
B 【解析】根据题意可得,被手捂住的多项式为$x^{2}+xy-(2xy-3y)=x^{2}+xy-2xy+3y=x^{2}-xy+3y.$
4. (教材习题第7题改编)化简:3(2x - y) - 2(3y - 2z) + (x + 3z).
答案:
解:原式$=6x-3y-6y+4z+x+3z=7x-9y+7z.$
5. (中考新考法·选择条件开放)给出三个多项式$\frac{2}{3}x^{2} + \frac{1}{4}x - 1,4x^{2} - \frac{3}{4}x - \frac{1}{3},-\frac{1}{3}x^{2} + x - \frac{1}{4},$请你任意选择其中两个进行加法或减法运算.
[此考法广东、山东等地中考已考查]
[此考法广东、山东等地中考已考查]
答案:
解:选择$\frac {2}{3}x^{2}+\frac {1}{4}x-1$和$-\frac {1}{3}x^{2}+x-\frac {1}{4}$进行加法运算如下:$\frac {2}{3}x^{2}+\frac {1}{4}x-1+(-\frac {1}{3}x^{2}+x-\frac {1}{4})$$=\frac {2}{3}x^{2}+\frac {1}{4}x-1-\frac {1}{3}x^{2}+x-\frac {1}{4}$$=\frac {1}{3}x^{2}+\frac {5}{4}x-\frac {5}{4}$.(答案不唯一)
6. (教材习题第8题改编)先化简,再求值:
(1)4(m + 1) + 2(2m^{2} + 3) - 3m^{2},其中$m = 5;(2)3x - 2(x + xy) + (\frac{3}{4}xy - 2y),其中x = 2,y = -\frac{1}{3}.$
(1)4(m + 1) + 2(2m^{2} + 3) - 3m^{2},其中$m = 5;(2)3x - 2(x + xy) + (\frac{3}{4}xy - 2y),其中x = 2,y = -\frac{1}{3}.$
答案:
解:
(1)原式$=4m+4+4m^{2}+6-3m^{2}$$=m^{2}+4m+10.$当$m=5$时,原式$=5^{2}+4×5+10=55;$
(2)原式$=3x-2x-2xy+\frac {3}{4}xy-2y$$=x-\frac {5}{4}xy-2y.$当$x=2,y=-\frac {1}{3}$时,原式$=2-\frac {5}{4}×2×(-\frac {1}{3})-2×(-\frac {1}{3})=\frac {7}{2}.$
(1)原式$=4m+4+4m^{2}+6-3m^{2}$$=m^{2}+4m+10.$当$m=5$时,原式$=5^{2}+4×5+10=55;$
(2)原式$=3x-2x-2xy+\frac {3}{4}xy-2y$$=x-\frac {5}{4}xy-2y.$当$x=2,y=-\frac {1}{3}$时,原式$=2-\frac {5}{4}×2×(-\frac {1}{3})-2×(-\frac {1}{3})=\frac {7}{2}.$
7. (教材练习第3题改编)如图是欣欣家的部分结构示意图,现计划用一堵隔墙将长为(a + b)米,宽为a米的长方形区域分成两部分,分别作为客厅和餐厅.则该区域的围墙总长度为
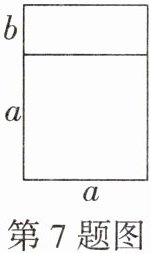
(5a+2b)
米.
答案:
$(5a+2b)$【解析】由题意得,该区域的围墙总长度为$2(a+b)+3a=2a+2b+3a=(5a+2b)$米.
8. 近年来,AI产业迅速发展,越来越多的AI产品进入我们的日常生活.“中医AI智能诊脉仪”可以辅助医生进行疾病诊断.某厂家现有A,B两种型号的诊脉仪,下表是该厂家某天的订单情况,则W的值为
|型号|A种|B种|
|单价/元|a|b|
|甲医院购买数量/台|3|4|
|乙医院购买数量/台|5|2|
|销售额/元|W|
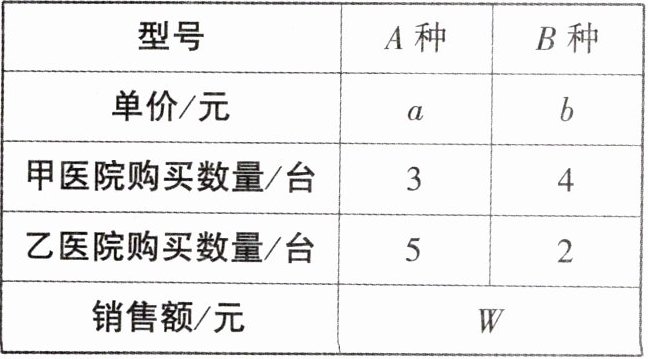
(8a+6b)
元.|型号|A种|B种|
|单价/元|a|b|
|甲医院购买数量/台|3|4|
|乙医院购买数量/台|5|2|
|销售额/元|W|

答案:
$(8a+6b)$【解析】甲医院需支付$(3a+4b)$元,乙医院需支付$(5a+2b)$元,则该厂商的销售额$W=3a+4b+5a+2b=(8a+6b)$元.
查看更多完整答案,请扫码查看


