第13页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
13. 下列说法正确的是 (
A.若$a<b$,则$\vert a\vert <\vert b\vert$
B.一个有理数的绝对值是它本身,则这个数一定是正数
C.任何一个有理数的绝对值一定不小于0
D.若$x>-2$,则$\vert x\vert >2$
C
)A.若$a<b$,则$\vert a\vert <\vert b\vert$
B.一个有理数的绝对值是它本身,则这个数一定是正数
C.任何一个有理数的绝对值一定不小于0
D.若$x>-2$,则$\vert x\vert >2$
答案:
C 【解析】当a=-3,b=-2时,a<b,|a|>|b|,A选项错误;0的绝对值是它本身,但0不是正数,B选项错误;任何一个有理数的绝对值一定不小于0,C选项正确;当x=-1时,x>-2,|x|=1<2,D选项错误.
14. 若$\vert a-3\vert和\vert b+1\vert$互为相反数,则$a,b$的值分别为 (
A.$3,-1$
B.$-3,1$
C.$-1,3$
D.$1,-3$
A
)A.$3,-1$
B.$-3,1$
C.$-1,3$
D.$1,-3$
答案:
A 【解析】由绝对值的非负性可得,|a-3|大于或等于0,|b+1|大于或等于0,又因为|a-3|与|b+1|互为相反数,所以|a-3|+|b+1|=0,所以a-3=0,b+1=0,即a=3,b=-1.
15. 将数$-0.2415$中的一个非零数字用数字8替换,使得所得的数最大,则被替换的数字是
5
.
答案:
5 【解析】因为一个负数的绝对值越大,其值越小;绝对值越小,其值越大,要使被替换后的值最大,则其绝对值要最小,所以替换后的数字为-0.2418,所以被替换的数字是5.
16. (教材习题第7题改编)广济桥是中国四大古桥之一,被桥梁专家茅以升誉为“世界上最早的启闭式桥梁”,广济桥全长518米.小明测量了5次桥长,测得的数据(单位:米)分别是:$518.4,517.8,518.2,517.9,517.7$.如果以518米为标准,超过标准长度的部分记为正,不足标准长度的部分记为负.
(1)试用正、负数在下表中表示出小明测得的数据与桥长的差(单位:米):
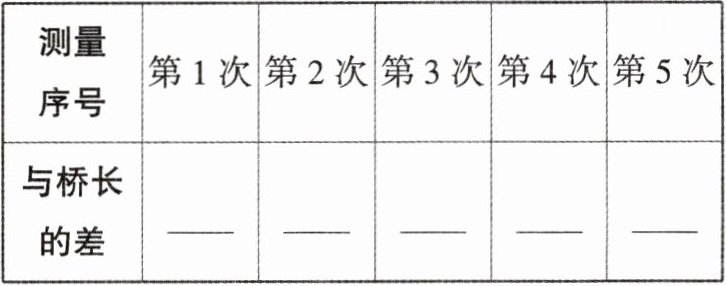
(2)请问哪次测得的结果最接近桥长?并说明理由.
(1)试用正、负数在下表中表示出小明测得的数据与桥长的差(单位:米):

测量序号 第1次 第2次 第3次 第4次 第5次 与桥长的差 +0.4 -0.2 +0.2 -0.1 -0.3
(2)请问哪次测得的结果最接近桥长?并说明理由.
第4次测得的结果最接近桥长,理由如下:因为|+0.4|=0.4,|-0.2|=0.2,|+0.2|=0.2,|-0.1|=0.1,|-0.3|=0.3,0.4>0.3>0.2>0.1,所以第4次测得的结果最接近桥长.
答案:
解:
(1)测量序号 第1次 第2次 第3次 第4次 第5次 与桥长的差 +0.4 -0.2 +0.2 -0.1 -0.3
(2)第4次测得的结果最接近桥长,理由如下:因为|+0.4|=0.4,|-0.2|=0.2,|+0.2|=0.2,|-0.1|=0.1,|-0.3|=0.3,0.4>0.3>0.2>0.1,所以第4次测得的结果最接近桥长.
(1)测量序号 第1次 第2次 第3次 第4次 第5次 与桥长的差 +0.4 -0.2 +0.2 -0.1 -0.3
(2)第4次测得的结果最接近桥长,理由如下:因为|+0.4|=0.4,|-0.2|=0.2,|+0.2|=0.2,|-0.1|=0.1,|-0.3|=0.3,0.4>0.3>0.2>0.1,所以第4次测得的结果最接近桥长.
17. 一题多设问 已知有理数$a,b,c,d$中,$a,d$为负数,$b,c$为正数,且$\vert c\vert >\vert b\vert >\vert d\vert >\vert a\vert$.
(1)画出数轴,并标出表示数$a,b,c,d$的点的大致位置;
(2)试将$a,c,d,-a,-c,-d$按照从小到大的顺序排列;
(3)比较$a,-b,-\vert c\vert,-(+d)$的大小;
(4)若有理数$m满足\vert b\vert <\vert m\vert$,试比较$b,-b,m$之间的大小关系.
(1)画出数轴,并标出表示数$a,b,c,d$的点的大致位置;
(2)试将$a,c,d,-a,-c,-d$按照从小到大的顺序排列;
(3)比较$a,-b,-\vert c\vert,-(+d)$的大小;
(4)若有理数$m满足\vert b\vert <\vert m\vert$,试比较$b,-b,m$之间的大小关系.
答案:
解:
(1)在数轴上标出表示数a,b,c,d的点大致位置如解图①所示:
(2)a,c,d,-a,-c,-d在数轴上的位置如解图②, 所以-c<d<a<-a<-d<c;
所以-c<d<a<-a<-d<c;
(3)在数轴上标出表示数a,-b,-|c|,-(+d)的点如解图, 所以-|c|<-b<a<-(+d);
所以-|c|<-b<a<-(+d);
(4)需分情况讨论:①若m=0,因为b>0,所以|b|>|m|,与题意矛盾,舍去;②若m>0,因为b>0,且|b|<|m|,所以m>b>-b;③若m<0,因为b>0,且|b|<|m|,所以b>-b>m.综上所述,当m>0时,m>b>-b;当m<0时,b>-b>m.
解:
(1)在数轴上标出表示数a,b,c,d的点大致位置如解图①所示:

(2)a,c,d,-a,-c,-d在数轴上的位置如解图②,
 所以-c<d<a<-a<-d<c;
所以-c<d<a<-a<-d<c;(3)在数轴上标出表示数a,-b,-|c|,-(+d)的点如解图,
 所以-|c|<-b<a<-(+d);
所以-|c|<-b<a<-(+d);(4)需分情况讨论:①若m=0,因为b>0,所以|b|>|m|,与题意矛盾,舍去;②若m>0,因为b>0,且|b|<|m|,所以m>b>-b;③若m<0,因为b>0,且|b|<|m|,所以b>-b>m.综上所述,当m>0时,m>b>-b;当m<0时,b>-b>m.
1. 若$\vert 4-a\vert +\vert b-2025\vert =0$,则$b-a$的值为 (
A.$2020$
B.$2021$
C.$2022$
D.$2023$
B
)A.$2020$
B.$2021$
C.$2022$
D.$2023$
答案:
B 【解析】因为|4-a|+|b-2025|=0,所以4-a=0,b-2025=0,所以a=4,b=2025,所以b-a=2025-4=2021.
2. 若$\vert 2-a\vert +\vert b-3\vert +\vert c\vert =0$,则$3a+2b+c$的值为______
12
.
答案:
12 【解析】因为|2-a|+|b-3|+|c|=0,所以2-a=0,b-3=0,c=0,所以a=2,b=3,所以3a+2b+c=6+6+0=12.
3. 当$2025-\vert x-2024\vert$取得最大值时,$x$的值为
2024
,此时取得的最大值为2025
.
答案:
2024,2025 【解析】因为|x-2024|的值大于或等于0,所以当|x-2024|的值取0时,2025-|x-2024|取得最大值,所以|x-2024|=0,所以x=2024,此时2025-|x-2024|=2025-0=2025.
查看更多完整答案,请扫码查看


