《2025年万唯中考情境题七年级数学上册苏科版》

9. 与$\frac {1}{2}÷(-5)$的计算结果相同的是 (C)
A.$(-5)÷\frac {1}{2}$
B.$\frac {1}{2}÷(-\frac {1}{5})$
C.$\frac {1}{2}×(-\frac {1}{5})$
D.$\frac {1}{2}×\frac {1}{5}$

答案： C

10. 跨学科情境 物理酒精凝固 已知在标准大气压下,酒精凝固的温度约为$-117^{\circ }C$,现有一杯酒精的温度是$8^{\circ }C$,将其放在一个制冷装置里,其温度每分钟可降低$2.5^{\circ }C$,则要使这杯酒精凝固需要的时间至少为 (A)
A.50 分钟
B.60 分钟
C.70 分钟
D.80 分钟

答案： A

11. (教材习题第 14 题改编) 一题多变
变式 1 结合数轴判断结论
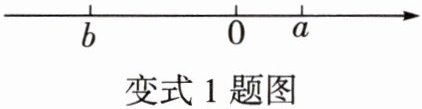
若有理数 a,b 在数轴上表示的点的位置如图所示,则下列结论一定成立的是 (D)

A.$a(a+b)＞0$
B.$\frac {a-b}{a+b}＞0$
C.$\frac {a}{b}＞0$
D.$\frac {|b|}{a}＞1$

答案： 变式 1 D 【解析】由题图可知$b＜0＜a$,$|b|＞|a|$,所以$a-b＞0$,$a+b＜0$,所以$a(a+b)＜0$,$\dfrac{a-b}{a+b}＜0$,$\dfrac{a}{b}＜0$,$\dfrac{|b|}{a}＞1$,所以结论正确的是 D 选项.变式 2 -2 【解析】因为$ab＜0$,所以$a,b$异号,所以$\dfrac{a}{b}=-\left(3÷ \dfrac{3}{2}\right)=-2$.

已知 a,b 是有理数,$|a|= 3,|b|= \frac {3}{2}$,且$ab＜0$,则$\frac {a}{b}$的值为-2.

答案： 【解析】：
本题主要考察有理数的除法运算以及绝对值的性质。
首先，根据题目给出的条件，知道$a$和$b$的绝对值分别为3和$\frac{3}{2}$，即 $|a| = 3$， $|b| = \frac{3}{2}$。
由此可以得出 $a$ 和 $b$ 的可能取值为 $a = \pm 3$， $b = \pm \frac{3}{2}$。
再根据题目条件 $ab ＜ 0$，即 $a$ 和 $b$ 必须异号。
当 $a = 3$ 时，$b$ 必须为 $-\frac{3}{2}$，此时 $\frac{a}{b} = \frac{3}{-\frac{3}{2}} = -2$。
当 $a = -3$ 时，$b$ 必须为 $\frac{3}{2}$，此时 $\frac{a}{b} = \frac{-3}{\frac{3}{2}} = -2$。
所以，无论 $a$ 和 $b$ 的具体取值如何，$\frac{a}{b}$ 的值都是 $-2$。
【答案】：
$-2$

12. 如图,小明有 5 张写着不同数字的卡片,请你按照要求抽取卡片,完成下列各题:

(1)从中任意抽取 2 张卡片,用两张卡片上的数字进行除法运算,所得商的最大值记为 a,求 a 的值;
(2)重新抽取 2 张卡片进行除法运算,所得商的最小值记为 b,求$\frac {a}{b}$的值.

答案： 解:
(1)因为两数相除,同号得正,异号得负,所以商的最大值$a$一定是两个同号的数相除得到的正数,两正数相除,被除数越大且除数越小时,商就越大,两负数相除,被除数越小且除数越大时,商就越大,所以当抽到两张正数卡片时,商最大得$4÷ 2=2$;当抽到两张负数卡片时,商最大得$(-5)÷ (-1)=5$,因为$5＞2$,所以商的最大值$a$的值为 5;
(2)因为两数相除,同号得正,异号得负,所以商的最小值$b$一定是两个异号的数相除得到的负数,两个异号的数相除,被除数的绝对值越大且除数的绝对值越小时,商就越小,所以当抽到绝对值最大的正数卡片和绝对值最小的负数卡片时,得$4÷ (-1)=-4$;当抽到绝对值最大的负数卡片和绝对值最小的正数卡片时,$(-5)÷ 2=-\dfrac{5}{2}$,因为$-4＜-\dfrac{5}{2}$,所以商的最小值$b$的值为$-4$,由
(1)知$a$的值为 5,所以$\dfrac{a}{b}=-\dfrac{5}{4}$.

13. 在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,例如:我们在讨论$|a|$的值时,就会对 a 进行分类讨论,当$a＞0$时,$|a|= a$;当$a= 0$时,$|a|= 0$;当$a＜0$时,$|a|= -a$,请尝试运用分类讨论思想,解答下面的问题.
(1)当$ab＞0,a+b＜0$时,先判断 a,b 的正负,再求$\frac {a}{|a|}+\frac {b}{|b|}$的值;
(2)当$abc≠0$时,求$\frac {a}{|a|}+\frac {b}{|b|}+\frac {c}{|c|}+\frac {abc}{|abc|}$的值.

答案： 解:
(1)因为$ab＞0$,$a+b＜0$,所以$a,b$同号且均为负数,所以$\dfrac{a}{|a|}+\dfrac{b}{|b|}=-1+(-1)=-2$;
(2)分情况讨论:①三个数均为负数,则原式$=(-1)+(-1)+(-1)+(-1)=-4$,②三个数中,两个为负,一个为正,取$a＜0$,$b＜0$,$c＞0$,则原式$=(-1)+(-1)+1+1=0$,③三个数中,一个为负,两个为正,取$a＜0$,$b＞0$,$c＞0$,则原式$=(-1)+1+1+(-1)=0$,④三个数均为正数,则原式$=1+1+1+1=4$,综上所述,当$abc≠0$时,$\dfrac{a}{|a|}+\dfrac{b}{|b|}+\dfrac{c}{|c|}+\dfrac{abc}{|abc|}$的值为-4 或 0 或 4.