《2025年万唯中考情境题七年级数学上册苏科版》

1. 如图,使用圆规比较线段AB和线段CD的长短,已知两个圆规的形态完全一致,则下列说法正确的是 (B)



A.$ AB ＜ CD $
B.$ AB ＞ CD $
C.$ AB = CD $
D.无法确定

答案： B

2. 学习生活情境 掷铅球 如图,运动会上小红,小丽,小美,小琴四名同学从投掷点投掷铅球,对应铅球落地的位置分别为A,B,C,D四点,则成绩最好的是 (B)

A.小红
B.小丽
C.小美
D.小琴

答案： B

3. (教材习题第4题改编)如图,用圆规判断三角形各边长度(保留作图痕迹),并在图中“○”内填上字母A,B,C,使得$ BC ＜ AB ＜ AC $.

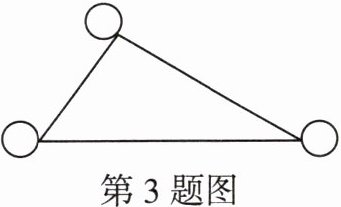
答案：
解:如解图,$BC\lt AB\lt AC$.

4. 下列关系式中与图形相符的式子是 (C)
A.$ AB = BD - CD $
B.$ AC = AB + CD $
C.$ AC - BC = AD - BD $
D.$ AB + BD = AD - CD $

答案： C

5. 已知点A,B,C在同一直线上,若$ AB = 10 cm $,$ BC = 6 cm $,则AC的长为4 cm 或 16 cm.

答案： 4 cm 或 16 cm

6. (教材练习第3题改编)如图,已知线段a,b,按要求用尺规进行作图,不写作法.
(1)作线段c,使得$ c = 2a $;
(2)作线段d,使得$ d = b - a $.

答案：
解:
(1)线段 c 如解图①; 【作法提示】作射线 AM,用圆规在射线 AM 上截取线段$AB=a$,在点 B 右边截取$BC=a$,则线段 AC 即为所求作线段 c.
(2)线段 d 如解图②. 【作法提示】作射线 EN,用圆规在射线 EN 上截取线段$EF=a$,线段$EH=b$,则线段 FH 即为所求作线段 d.

7. 如图,已知点B,C在线段AD上,$ AC = BD $.
(1)AB=CD(填“＞”“＜”或“=”)；
(2)若$ BC:CD = 3:1 $,$ AB = 3 $,求AD的长.

解:由(1)知$AB=CD$,因为$AB=3$,所以$CD=AB=3$,因为$BC:CD=3:1$,所以$BC=3CD=9$,所以$AD=AB+BC+CD=3+9+3=15.$

答案： 解:
(1)=;
(2)由
(1)知$AB=CD$,
因为$AB=3$,所以$CD=AB=3$,
因为$BC:CD=3:1$,所以$BC=3CD=9$,
所以$AD=AB+BC+CD=3+9+3=15.$

8. 如图,P为线段MN上一点,Q为线段MN的中点,已知线段$ QN = 6 $,$ MP = 4 $,则线段PQ的长为 (B)
A.1
B.2
C.3
D.4

答案： B

9. (教材习题第6题改编) 一题多变
变式1 改点B为中点
如图,B是线段AD的中点,C是线段BD的中点,若$ BC = 2 $,则线段AD的长为 (C)


A.4
B.6
C.8
D.10
变式2 改变线段关系求长度
如图,线段$ AB = 15 $,点C在线段AB上,且$ BC = \frac{1}{4}AC $,D是AC的中点,则BD的长为9.

答案： 变式1 C 变式2 9