《2025年万唯中考情境题七年级数学上册苏科版》

1. 若$∠A = 40^{\circ}38'$,则$∠A$的补角的度数为(C)
A.$39^{\circ}22'$
B.$50^{\circ}38'$
C.$139^{\circ}22'$
D.$150^{\circ}38'$

答案： C

2. (教材活动改编)将一副三角板按下列4种方式摆放,则其中使$∠α和∠β$互余的摆放方式是(B)

答案： B

3. (教材练习第3题改编)已知$∠1$是锐角,$∠1与∠2$互余,$∠1与∠3$互补,则$∠3 - ∠2$的值为90°.

答案： 90°

4. (教材例2改编)一个角的度数比它的余角度数的$\frac{1}{2}还少9^{\circ}$,求这个角的补角的度数为$156^{\circ}$.

答案： 【解析】：
本题主要考查余角和补角的概念及运算。
根据余角的定义，两个角的和为$90^{\circ}$，则它们互为余角。
设这个角为$x^{\circ}$，则其余角为$(90 - x)^{\circ}$。
根据题意，这个角的度数比它的余角度数的$\frac{1}{2}$还少$9^{\circ}$，可以列出方程：
$x = \frac{1}{2}(90 - x) - 9$，
展开并整理得：
$2x = 90 - x - 18$，
$3x = 72$，
$x = 24$，
所以，这个角的度数为$24^{\circ}$。
根据补角的定义，两个角的和为$180^{\circ}$，则它们互为补角。
因此，这个角的补角度数为：
$180^{\circ} - 24^{\circ} = 156^{\circ}$。
【答案】：
$156^{\circ}$。

5. 如果$∠1和∠2$互补,且$∠1 ＞ ∠2$,则下列表示$∠2$的余角的式子:①$∠2 - 90^{\circ}$;②$90^{\circ} - ∠1$;③$\frac{1}{2}(∠1 + ∠2)$;④$\frac{1}{2}(∠1 - ∠2)$,其中正确的是______④.

答案： ④

6. 已知$∠A + ∠B = 180^{\circ}$,$∠A + ∠C = 180^{\circ}$,则$∠B = ∠C$,理由是(B)
A.同角的余角相等
B.同角的补角相等
C.等角的余角相等
D.等角的补角相等

答案： B

7. (教材练习第2题改编)如图,$A$,$O$,$B$三点共线,$∠BOD = ∠COE = 90^{\circ}$,图中与$∠AOC$互补的角有(B)
A.1个
B.2个
C.3个
D.4个

答案： B

8. 如图,在三角形$ABC$中,$∠BAC = ∠ADC = 90^{\circ}$,$∠DAC = 58^{\circ}$,则$∠B$的度数为58$^{\circ}$.

答案： 【解析】：本题可根据直角三角形的性质以及余角的性质来求解$\angle B$的度数。
在$Rt\triangle ADC$中，已知$\angle ADC = 90^{\circ}$，$\angle DAC = 58^{\circ}$，根据直角三角形两锐角互余，可求出$\angle C$的度数。
因为$\angle C$与$\angle DAC$是$\triangle ADC$的两个锐角，所以$\angle C + \angle DAC = 90^{\circ}$，则$\angle C = 90^{\circ} - \angle DAC = 90^{\circ} - 58^{\circ} = 32^{\circ}$。
在$Rt\triangle ABC$中，$\angle BAC = 90^{\circ}$，同样根据直角三角形两锐角互余，$\angle B + \angle C = 90^{\circ}$，已经求得$\angle C = 32^{\circ}$，所以$\angle B = 90^{\circ} - \angle C = 90^{\circ} - 32^{\circ} = 58^{\circ}$。
【答案】：$58$

9. (教材活动改编)将一副三角板按如图所示的方式摆放,两个三角板的直角顶点重合于点$O$,则$∠BOC + ∠AOD = $180$^{\circ}$.

答案： 180

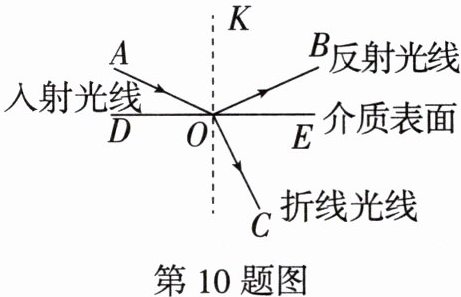
10. 跨学科情境 物理光的折射与反射 如图,一束光线$AO照射到某种介质表面DE$时,发生了折射和反射现象.已知$∠AOK = ∠BOK$,$∠KOE = 90^{\circ}$,若$∠COE = 65^{\circ}$,$∠BOE与∠COE$互余,则$∠AOK$的度数为______.

65°

答案： 解：
∵∠BOE与∠COE互余，∠COE=65°，
∴∠BOE=90°-∠COE=90°-65°=25°。
∵∠KOE=90°，
∴∠KOB=∠KOE-∠BOE=90°-25°=65°。
∵∠AOK=∠BOK，
∴∠AOK=65°。
答案：65°

11. (中考新考法·阅读理解题)定义:若$\frac{1}{2}∠A + ∠B = 90^{\circ}$,则将$∠B称为∠A$的“半余角”.
(1)若$∠1 = 50^{\circ}$,则$∠1$的“半余角”的度数为______$65^{\circ}$;
(2)若$∠1$的“半余角”与$∠2$的“半余角”互余,试判断$∠1与∠2$之间的数量关系;$\angle 1 + \angle 2 = 180^{\circ}$
(3)若$∠1与∠2$互补,$∠3是∠2$的“半余角”,$∠3与∠4$互余,试判断$∠4是否是∠1$的“半余角”? 并说明理由.$\angle 4$是$\angle 1$的“半余角”，理由如下：因为$\angle 1$与$\angle 2$互补，所以$\angle 1 + \angle 2 = 180^{\circ}$。因为$\angle 3$是$\angle 2$的“半余角”，所以$\frac{1}{2}\angle 2 + \angle 3 = 90^{\circ}$，即$\angle 3 = 90^{\circ} - \frac{1}{2}\angle 2$。因为$\angle 3$与$\angle 4$互余，所以$\angle 3 + \angle 4 = 90^{\circ}$，则$\angle 4 = 90^{\circ} - \angle 3 = 90^{\circ} - (90^{\circ} - \frac{1}{2}\angle 2) = \frac{1}{2}\angle 2$。又因为$\angle 1 + \angle 2 = 180^{\circ}$，所以$\angle 2 = 180^{\circ} - \angle 1$，所以$\angle 4 = \frac{1}{2}(180^{\circ} - \angle 1) = 90^{\circ} - \frac{1}{2}\angle 1$，即$\frac{1}{2}\angle 1 + \angle 4 = 90^{\circ}$，所以$\angle 4$是$\angle 1$的“半余角”。

答案： 【解析】：
本题主要考察了对新定义的理解和应用，以及余角、补角的性质。
(1)根据“半余角”的定义，若$\frac{1}{2}\angle A + \angle B = 90^{\circ}$，则$\angle B$是$\angle A$的“半余角”。
对于$\angle 1 = 50^{\circ}$，设其“半余角”为$\angle B$，则有：
$\frac{1}{2} × 50^{\circ} + \angle B = 90^{\circ}$
解得：$\angle B = 90^{\circ} - 25^{\circ} = 65^{\circ}$
(2)设$\angle 1$的“半余角”为$\angle B$，$\angle 2$的“半余角”为$\angle C$。
根据题意，$\angle B + \angle C = 90^{\circ}$。
由“半余角”的定义，我们有：
$\frac{1}{2}\angle 1 + \angle B = 90^{\circ}$
$\frac{1}{2}\angle 2 + \angle C = 90^{\circ}$
将$\angle B = 90^{\circ} - \frac{1}{2}\angle 1$和$\angle C = 90^{\circ} - \frac{1}{2}\angle 2$代入$\angle B + \angle C = 90^{\circ}$，得：
$90^{\circ} - \frac{1}{2}\angle 1 + 90^{\circ} - \frac{1}{2}\angle 2 = 90^{\circ}$
化简得：$\angle 1 + \angle 2 = 180^{\circ}$
(3)设$\angle 3$是$\angle 2$的“半余角”，$\angle 4$与$\angle 3$互余。
根据题意，$\angle 1 + \angle 2 = 180^{\circ}$（互补）。
由“半余角”的定义，我们有：
$\frac{1}{2}\angle 2 + \angle 3 = 90^{\circ}$
又因为$\angle 3 + \angle 4 = 90^{\circ}$（互余），
所以$\angle 4 = 90^{\circ} - \angle 3$
代入$\angle 3 = 90^{\circ} - \frac{1}{2}\angle 2$，得：
$\angle 4 = 90^{\circ} - (90^{\circ} - \frac{1}{2}\angle 2) = \frac{1}{2}\angle 2$
又因为$\angle 1 + \angle 2 = 180^{\circ}$，所以$\angle 2 = 180^{\circ} - \angle 1$，
代入$\angle 4 = \frac{1}{2}\angle 2$，得：
$\angle 4 = \frac{1}{2}(180^{\circ} - \angle 1) = 90^{\circ} - \frac{1}{2}\angle 1$
这正是“半余角”的定义，所以$\angle 4$是$\angle 1$的“半余角”。
【答案】：
(1)$65^{\circ}$
(2)$\angle 1 + \angle 2 = 180^{\circ}$
(3)$\angle 4$是$\angle 1$的“半余角”，理由如上。