第83页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
5. 将如图①所示的图形旋转,亮亮得到的几何体如图②所示,天天得到的几何体如图③所示.
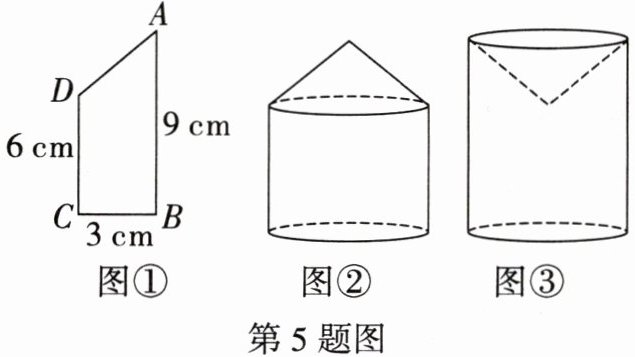
(1)图②是由图①中的图形绕着
(2)上述几何体的形成过程蕴含的数学知识是
(3)分别求图②和图③中几何体的体积.(π取 3,$V_{圆柱}= πr^{2}\cdot h$,$V_{圆锥}= \frac {1}{3}πr^{2}\cdot h$)
解:图②体积:$V=π×3^{2}×6+\frac {1}{3}π×3^{2}×(9-6)=3×9×6+\frac {1}{3}×3×9×3=162+27=189(cm^{3})$
图③体积:$V=π×3^{2}×9-\frac {1}{3}π×3^{2}×(9-6)=3×9×9-\frac {1}{3}×3×9×3=243-27=216(cm^{3})$

(1)图②是由图①中的图形绕着
AB
所在的直线旋转而成,图③是由图①中的图形绕着BC
所在的直线旋转而成;(2)上述几何体的形成过程蕴含的数学知识是
面动成体
;(3)分别求图②和图③中几何体的体积.(π取 3,$V_{圆柱}= πr^{2}\cdot h$,$V_{圆锥}= \frac {1}{3}πr^{2}\cdot h$)
解:图②体积:$V=π×3^{2}×6+\frac {1}{3}π×3^{2}×(9-6)=3×9×6+\frac {1}{3}×3×9×3=162+27=189(cm^{3})$
图③体积:$V=π×3^{2}×9-\frac {1}{3}π×3^{2}×(9-6)=3×9×9-\frac {1}{3}×3×9×3=243-27=216(cm^{3})$
答案:
(1)AB;BC
(2)面动成体
(3)解:图②体积:$V=π×3^{2}×6+\frac {1}{3}π×3^{2}×(9-6)=3×9×6+\frac {1}{3}×3×9×3=162+27=189(cm^{3})$
图③体积:$V=π×3^{2}×9-\frac {1}{3}π×3^{2}×(9-6)=3×9×9-\frac {1}{3}×3×9×3=243-27=216(cm^{3})$
(1)AB;BC
(2)面动成体
(3)解:图②体积:$V=π×3^{2}×6+\frac {1}{3}π×3^{2}×(9-6)=3×9×6+\frac {1}{3}×3×9×3=162+27=189(cm^{3})$
图③体积:$V=π×3^{2}×9-\frac {1}{3}π×3^{2}×(9-6)=3×9×9-\frac {1}{3}×3×9×3=243-27=216(cm^{3})$
6. 2025 年是抗日战争胜利 80 周年,在如图所示的正方体展开图上写下“弘扬革命精神”六个字,则在原正方体中与“精”字相对的是(
A.弘
B.扬
C.革
D.神
C
)A.弘
B.扬
C.革
D.神
答案:
【解析】:本题考查正方体展开图的相对面。在正方体的展开图中,相对的面之间一定相隔一个正方形。观察展开图可知,“弘”与“神”相对,“扬”与“命”相对,“革”与“精”相对。
【答案】:C。
【答案】:C。
7. 如图是某几何体的平面展开图,已知$r= 2$,AB 长等于展开图中圆的直径,则四边形 ABCD 的周长为______.(结果保留 π)
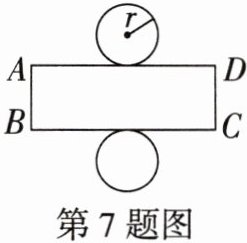

8 + 8π
答案:
解:
∵ 圆的半径 $ r = 2 $,
∴ 圆的直径为 $ 2r = 4 $,
∴ $ AB = 4 $。
∵ 该展开图由两个圆和一个矩形组成,
∴ 矩形的一边长等于圆的周长,即 $ AD = 2\pi r = 2\pi × 2 = 4\pi $。
∵ 四边形 $ ABCD $ 是矩形,
∴ $ AB = CD = 4 $,$ AD = BC = 4\pi $。
∴ 四边形 $ ABCD $ 的周长为 $ 2(AB + AD) = 2(4 + 4\pi) = 8 + 8\pi $。
$ 8 + 8\pi $
∵ 圆的半径 $ r = 2 $,
∴ 圆的直径为 $ 2r = 4 $,
∴ $ AB = 4 $。
∵ 该展开图由两个圆和一个矩形组成,
∴ 矩形的一边长等于圆的周长,即 $ AD = 2\pi r = 2\pi × 2 = 4\pi $。
∵ 四边形 $ ABCD $ 是矩形,
∴ $ AB = CD = 4 $,$ AD = BC = 4\pi $。
∴ 四边形 $ ABCD $ 的周长为 $ 2(AB + AD) = 2(4 + 4\pi) = 8 + 8\pi $。
$ 8 + 8\pi $
8. 下列图形是某些几何体的平面展开图,则这些几何体分别是(
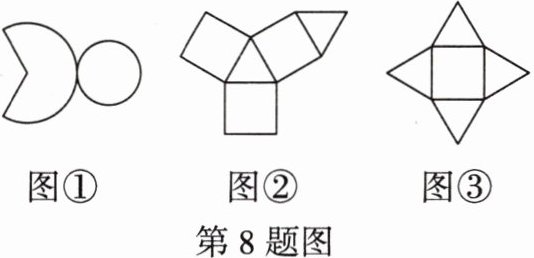
A.圆柱,三棱柱,三棱锥
B.圆柱,四棱柱,四棱锥
C.圆锥,三棱柱,四棱锥
D.圆锥,四棱柱,三棱锥
C
)
A.圆柱,三棱柱,三棱锥
B.圆柱,四棱柱,四棱锥
C.圆锥,三棱柱,四棱锥
D.圆锥,四棱柱,三棱锥
答案:
解:图①由一个扇形和一个圆形组成,是圆锥的平面展开图;图②由两个三角形和三个长方形组成,是三棱柱的平面展开图;图③由一个正方形和四个三角形组成,是四棱锥的平面展开图。
答案:C
答案:C
9. 如图①为一个长方体包装盒,其底面是一个边长为 4 cm 的正方形.将这个包装盒沿某些棱剪开后展开,如图②所示,字母均在盒子外表面.
(1)若 c 面为正面,从左面看是 e 面,则上面为
(2)若被剪开的棱的棱长和为 40 cm,求这个长方体的体积;
(3)将这个长方体按另外一种方式展开,请你画出与图②不一样的展开图.
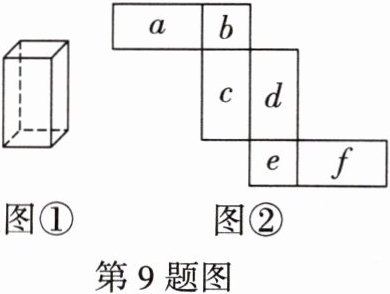
(1)若 c 面为正面,从左面看是 e 面,则上面为
f
面;(2)若被剪开的棱的棱长和为 40 cm,求这个长方体的体积;
解:设长方体的高为 $ h $ cm。
底面是边长为 4 cm 的正方形,展开图中被剪开的棱有 7 条(4 条高,2 条长,1 条宽,或其他组合,总棱长和为 $ 4h + 4×2 + 4×1 = 4h + 12 $,此处根据展开图特征,实际剪开棱为 4 条高和 3 条底面边长,即 $ 4h + 3×4 $)。
由题意:$ 4h + 3×4 = 40 $
解得 $ h = 7 $
体积 $ V = 4×4×7 = 112 \, \text{cm}^3 $
底面是边长为 4 cm 的正方形,展开图中被剪开的棱有 7 条(4 条高,2 条长,1 条宽,或其他组合,总棱长和为 $ 4h + 4×2 + 4×1 = 4h + 12 $,此处根据展开图特征,实际剪开棱为 4 条高和 3 条底面边长,即 $ 4h + 3×4 $)。
由题意:$ 4h + 3×4 = 40 $
解得 $ h = 7 $
体积 $ V = 4×4×7 = 112 \, \text{cm}^3 $
(3)将这个长方体按另外一种方式展开,请你画出与图②不一样的展开图.
(展开图略,需画出与图②不同的长方体表面展开图,例如“一四一”型不同排列或“二三一”型等)

答案:
(1) f
(2) 解:设长方体的高为 $ h $ cm。
底面是边长为 4 cm 的正方形,展开图中被剪开的棱有 7 条(4 条高,2 条长,1 条宽,或其他组合,总棱长和为 $ 4h + 4×2 + 4×1 = 4h + 12 $,此处根据展开图特征,实际剪开棱为 4 条高和 3 条底面边长,即 $ 4h + 3×4 $)。
由题意:$ 4h + 3×4 = 40 $
解得 $ h = 7 $
体积 $ V = 4×4×7 = 112 \, \text{cm}^3 $
(3) (展开图略,需画出与图②不同的长方体表面展开图,例如“一四一”型不同排列或“二三一”型等)
(1) f
(2) 解:设长方体的高为 $ h $ cm。
底面是边长为 4 cm 的正方形,展开图中被剪开的棱有 7 条(4 条高,2 条长,1 条宽,或其他组合,总棱长和为 $ 4h + 4×2 + 4×1 = 4h + 12 $,此处根据展开图特征,实际剪开棱为 4 条高和 3 条底面边长,即 $ 4h + 3×4 $)。
由题意:$ 4h + 3×4 = 40 $
解得 $ h = 7 $
体积 $ V = 4×4×7 = 112 \, \text{cm}^3 $
(3) (展开图略,需画出与图②不同的长方体表面展开图,例如“一四一”型不同排列或“二三一”型等)
查看更多完整答案,请扫码查看


