《2025年万唯中考情境题七年级数学上册苏科版》

1. 有一列数字：3,5,8,13,21,…,则第7个数字为(D)
A.28
B.34
C.43
D.55

答案： D 【解析】从数字排列规律可以得到，3+5=8，5+8=13，8+13=21，则第6个数字为13+21=34，第7个数字为21+34=55.

2. (教材练习改编)用火柴棒进行如下规律拼图,则第8个图形所用的火柴棒的数量为(C)
A.21
B.23
C.25
D.29

答案： C 【解析】由题图可以看出，第1个图形用了4根火柴棒；第2个图形用4+3=7(根)火柴棒；第3个图形用4+3×2=10(根)火柴棒；…，则第8个图形用4+3×7=25(根)火柴棒.

3. 观察下表x与y的对应关系：

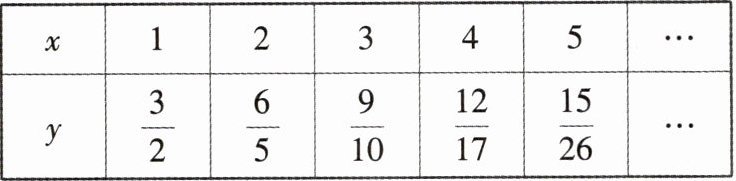
当x= 7时,y的值为(C)
A.$\dfrac{21}{47}$
B.$\dfrac{21}{49}$
C.$\dfrac{21}{50}$
D.$\dfrac{21}{53}$

答案： C 【解析】由题可知，y分子可表示为3x，分母可表示为$x^{2}+1$，所以y=$\frac{3x}{x^{2}+1}$，当x=7时,y=$\frac{3×7}{7^{2}+1}=\frac{21}{50}$.

4. 北宋数学家沈括的主要数学成就之一为隙积术,即把同样的物品层层堆积,各层都是一个长方形,且逐层在长、宽方面各减少一个,求其总数。如图,从上向下数第1层有(5×4)个球,第2层有(6×5)个球,第3层有(7×6)个球,则第7层有110个球。

答案： 110【解析】由题意可知，第7层有11×10=110(个)球.

5. 古希腊著名的毕达哥拉斯学派把1,3,6,10,…,这样的数称为三角形数,而把1,4,9,16,…,这样的数称为正方形数。如图,任何一个大于1的正方形数都可以看作是两个相邻三角形数之和。下列式子中：①13= 3+10；②25= 9+16；③36= 15+21；④49= 18+31,符合这一规律的是______。(填序号)

③

答案： ③ 【解析】13不是正方形数，①不符合题意；9和16为相邻的两个正方形数，不是三角形数，②不符合题意；从题图中可以看出，接下来的三角形数为15,21，正方形数为25,36，故18不是三角形数④不符合题意.

6. 将一串数字按照下图所示的规律排列,则2025的位置应该为(C)
A.位置A
B.位置B
C.位置C
D.位置D

答案： C 【解析】由题图可知，在A处的数被4除余3，在B处的数被4除余2，在C处的数被4除余1，在D处的数被4整除.2025÷4=506……1，所以2025的位置应该为位置C.

7. 如图,平面中的一条直线最多将平面分为2部分,两条直线最多将平面分为4部分,三条直线最多将平面分为7部分,按照此规律可知,七条直线最多将平面分为29部分。

答案： 29 【解析】因为2=$\frac{1×(1+1)}{2}+1$，4=$\frac{2×(2+1)}{2}+1$，7=$\frac{3×(3+1)}{2}+1$，所以七条直线最多将平面分为$\frac{7×(7+1)}{2}+1=29$(部分).

8. (教材素材改编)地球被厚厚的大气层包围,大气产生的压强叫作大气压强,大气压强的值随海拔高度的变化而变化,明明为了解其变化规律,查阅资料得到如下表格：

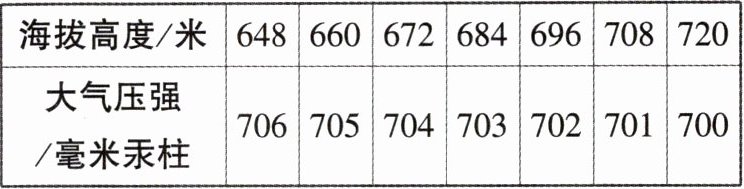
根据上表,回答下列问题：
(1)你能发现大气压强随海拔高度变化的特点吗?
(2)若明明假期爬山时,在山脚下测得大气压强为700毫米汞柱,爬到山顶时,测得大气压强为597毫米汞柱,求明明所爬山的高度。

答案： 解：
(1)海拔每升高12米，大气压强降低1毫米汞柱；
(2)由题意得，山脚与山顶的大气压强差为700-597=103(毫米汞柱)，所以明明所爬山的高度为103×12=1236(米).