《2025年万唯中考情境题七年级数学上册苏科版》

10. (教材探究改编)三个连续的偶数,m 是最小的一个,则这三个数的和是 (D)
A.3m
B.$m + 4$
C.$m + 6$
D.$3m + 6$

答案： 【解析】：
题目考查了合并同类项的知识点，特别是关于连续偶数的表示和求和。
首先，根据题目，$m$ 是三个连续偶数中最小的一个。
那么，下一个偶数就是 $m + 2$，接着的下一个偶数就是 $m + 4$。
要求这三个数的和，我们需要将这三个数相加。
即：$m + (m + 2) + (m + 4)$，
去括号得：$m + m + 2 + m + 4$，
合并同类项得：$3m + 6$。
【答案】：
D. $3m + 6$。

11. 已知 $3m^{2}n^{a}$ 与 $2m^{b}n^{5}$ 是同类项,则 $a + b$ 的值为7.

答案： 【解析】：
本题考查同类项的定义，即两个代数式所含的字母相同，且相同字母的指数也相同，则这两个代数式就是同类项。
根据题意，$3m^{2}n^{a}$与$2m^{b}n^{5}$是同类项，所以它们的字母部分和相应的指数必须相同。
对比$m$的指数，我们得到$b = 2$；
对比$n$的指数，我们得到$a = 5$。
所以，$a + b = 5 + 2 = 7$。
【答案】：
$7$

12. 如图是某月的月历,用“X”字型阴影框住 5 个数字,设中心的数字为 a,则所框住的这 5 个数字之和是5a.(用含 a 的代数式表示)

答案： 【解析】：
第12题：
观察月历中用“X”字型阴影框住的5个数字，设中心的数字为a。
根据月历的排列规律，可以得到这5个数字分别为：$a-7$，$a-1$ ，a，$a+1$，$a+7$。
则这5个数字之和为：
$(a-7)+(a-1)+a+(a+1)+(a+7)$
$=a-7+a-1+a+a+1+a+7$
$=5a$

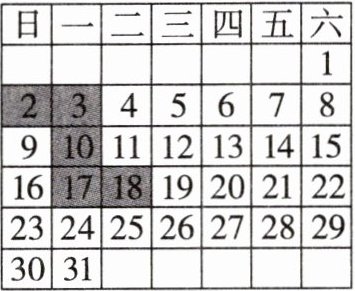
13. 如图,用“Z”字型阴影框住月历中的 5 个数字,设中心的数字为 b,则所框住的这 5 个数字之和是______.(用含 b 的代数式表示)

答案： 第13题：
观察月历中用“Z”字型阴影框住的5个数字，设中心的数字为b。
根据月历的排列规律，可以得到这5个数字分别为：$b-8$，$b-6$，b，$b-1$，$b+1$。
则这5个数字之和为：
$(b-8)+(b-6)+b+(b-1)+(b+1)$
$=b-8+b-6+b+b-1+b+1$
$=5b-14+1-1$
$=5b-14$

14. 已知多项式 $A = 2x^{2} - mx + 3,B = 3nx^{2} - 2x + 1$.
(1)若 $\frac{1}{2}a^{m}bc^{2}$ 与 $3a^{2}bc^{n}$ 的差为单项式,求 $A + B$ 的值;
(2)若 $A + B$ 的值与 x 的取值无关,求 $m - 3n$ 的值.

答案： 答案略

15. 数学文化情境 数学符号 在现代的数学符号统一之前,我国在清朝学堂的课本《代微积拾级》中还用“$\frac{五}{乙^{二}} \top \frac{三}{丙^{二}} \perp \frac{二七}{甲^{二}乙^{二}}$”来表示代数式 $\frac{b^{2}}{5} - \frac{c^{2}}{3} + \frac{a^{2}b^{2}}{27}$,观察其中的规律,化简“$\frac{二}{甲^{二}} \perp \frac{七}{乙^{二}} \top \frac{四}{三甲^{二}}$”的结果为______$\frac{7a^{2}}{12}-\frac{b^{2}}{7}$.

答案： 解：由题意知，“甲”对应“a”，“乙”对应“b”，“二”对应“2”，“七”对应“7”，“四”对应“4”，“三”对应“3”，“⊥”对应“-”，“⊤”对应“+”，分数线上下数字交换位置。
则“$\frac{二}{甲^{二}}$”表示$\frac{a^{2}}{2}$，“$\frac{七}{乙^{二}}$”表示$\frac{b^{2}}{7}$，“$\frac{四}{三甲^{二}}$”表示$\frac{a^{2}}{4×3}=\frac{a^{2}}{12}$（此处“三甲²”应理解为“3×甲²”，分子为“四”即4，故原符号表示$\frac{a^{2}}{3×4}=\frac{a^{2}}{12}$）。
所以原式为$\frac{a^{2}}{2}-\frac{b^{2}}{7}+\frac{a^{2}}{12}$。
合并同类项：$\frac{a^{2}}{2}+\frac{a^{2}}{12}=\frac{6a^{2}}{12}+\frac{a^{2}}{12}=\frac{7a^{2}}{12}$。
结果为$\frac{7a^{2}}{12}-\frac{b^{2}}{7}$。
$\frac{7a^{2}}{12}-\frac{b^{2}}{7}$

1. 若代数式 $x^{2}y - mxy + x^{2} - 3xy + y^{2}$ 合并同类项后不含 xy 项,则 m 的值为 (A)
A.- 3
B.- 1
C.1
D.3

答案： 【解析】：
本题主要考查合并同类项的知识点。
在代数式 $x^{2}y - mxy + x^{2} - 3xy + y^{2}$ 中，我们需要找到所有包含 $xy$ 的项，并将它们合并。
代数式中包含 $xy$ 的项有 $-mxy$ 和 $-3xy$。
合并后，$xy$ 项的系数为 $-m - 3$。
题目要求合并同类项后不含 $xy$ 项，即 $-m - 3 = 0$。
解这个方程，我们得到 $m = -3$。
【答案】：
A

2. 已知关于 x 的多项式 $2x^{2} + mx + 4 - nx^{2} - \frac{1}{3}x + 1$ 的值与 x 的取值无关,则 $n - 3m$ 的值为1.

答案： 【解析】：
首先，将多项式中的同类项合并，即合并$x^2$的系数和x的系数。
多项式 $2x^{2} + mx + 4 - nx^{2} - \frac{1}{3}x + 1$ 合并同类项后得到：
$(2 - n)x^{2} + \left(m - \frac{1}{3}\right)x + 5$
由于多项式的值与x的取值无关，那么x的系数必须都为0，即：
$2 - n = 0$
$m - \frac{1}{3} = 0$
解这两个方程，得到：
$n = 2$
$m = \frac{1}{3}$
最后，求 $n - 3m$ 的值：
$n - 3m = 2 - 3 × \frac{1}{3} = 2 - 1 = 1$
【答案】：
1