《2025年万唯中考情境题七年级数学上册苏科版》

9. 如图所示的素描图中,不存在的几何体是(D)
A.圆锥
B.长方体
C.圆柱
D.球

答案： D

10. 已知一个几何体共有12个顶点、8个面,则这个几何体可能是 (A)
A.六棱柱
B.五棱柱
C.六棱锥
D.五棱锥

答案： A

11. (教材练习第1题改编)如图①是神舟十九号载人飞船,图②是其整流罩的示意图.整流罩的示意图可以看成是由圆锥和圆柱两部分几何体组成的.

答案： 圆锥,圆柱

12. 不透明袋子中装有一个棱柱,小华和小张说出了关于这个棱柱的一些信息.小华:它有12个顶点;小张:所有侧面的面积之和是$180cm^2.$
(1)该棱柱是六棱柱;
(2)若该棱柱的底面边长均为5cm,求每条侧棱长.
解:(2)因为底面边长均为5 cm,所以底面周长为5×6=30(cm),所以每条侧棱长是180÷30=6(cm).

答案： 解:
(1)六;
(2)因为底面边长均为5 cm,所以底面周长为5×6=30(cm),所以每条侧棱长是180÷30=6(cm).

13. (综合与实践·图形变化探究)十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间满足一定的数量关系,被称为多面体欧拉公式.现将一正方体用不同的平面截去一块,得到如下简单多面体:

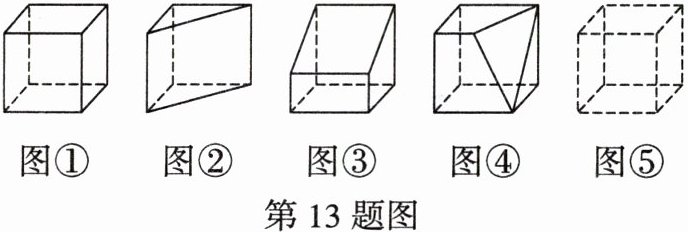
(1)观察上面多面体,填写表格空缺的内容:

|
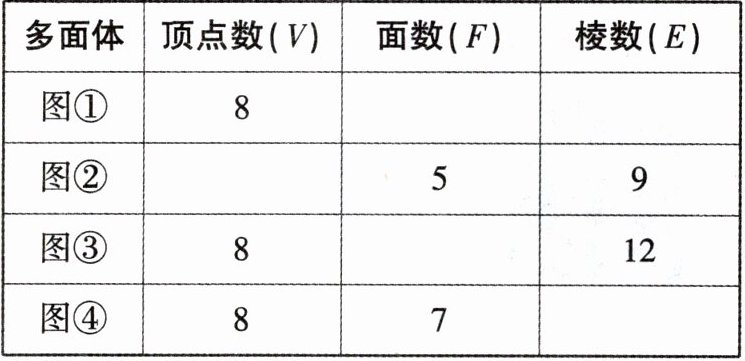
(2)通过填表可以总结出顶点数(V)、面数(F)和棱数(E)之间的数量关系是______,并在图⑤中画出一种不同的截法来验证结论的正确性;
(3)若一个多面体有2024个顶点,4047条棱,试求出它的面数.

答案：
解:
(1)补充表格如下;多面体 顶点数(V) 面数(F) 棱数(E)图① 8 6 12图② 6 5 9图③ 8 6 12图④ 8 7 13
(2)V+F-E=2;【解法提示】观察上表,即可总结出顶点数(V)、面数(F)和棱数(E)之间的数量关系是:V+F-E=2.如解图所示截法: 则该多面体的顶点数(V)为10,面数(F)为7,棱数(E)为15,又因为10+7-15=2,所以结论“V+F-E=2”仍然成立(答案不唯一,合理即可);
(3)由
(2)知,V+F-E=2,当V=2024,E=4047时,F=2025,所以它的面数为2025.