《2025年万唯中考情境题七年级数学上册苏科版》

11. 社会热点情境 春晚 2025年春晚作为春节申遗成功后的首届春晚,整场晚会的主题为“巳巳如意,生生不息”,如图为春晚的主标识,其采用的数学变换是 (B)



A.平移
B.旋转
C.对称
D.翻折

答案： B

12. 将如图所示的图形绕虚线旋转一周后,得到的几何体与下列花瓶形状最相似的是 (C)

答案： C

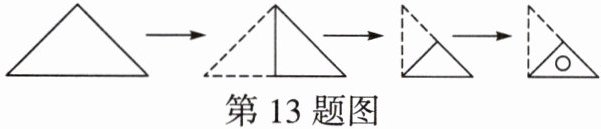
13. (教材活动改编)如图,将一个等腰三角形纸片按下列顺序折叠,在折叠后的纸片上剪去一个圆,然后将纸片展开,得到的图形是 (C)

答案： C

14. “鸣雨既过渐细微,映空摇飏如丝飞”,这句诗中描写雨滴滴下来形成雨丝,用数学知识解释为点动成线.

答案： 点动成线

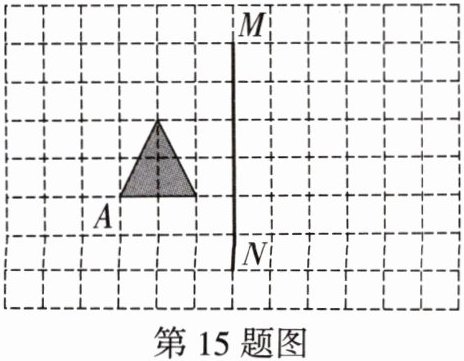
15. 如图,三角形的各个顶点均在正方形网格线的格点上,按要求解决下列问题：
(1)画出三角形绕A点逆时针旋转90°后得到的三角形；
(2)画出三角形沿直线MN翻折后得到的三角形(点A的对应点为点A').

答案：
解:
(1)如解图①即为所求图形;

(2)如解图②即为所求图形.

16. 已知一个长为5,宽为4的长方形,将其绕一条边所在的直线旋转一周可以得到一个圆柱,求这个圆柱的最大体积. (结果保留π,圆柱的体积计算公式为$V = πr^2h)$

答案： 解:分两种情况讨论:①绕长方形的长旋转时,圆柱的体积$ V=\pi×4^{2}×5 = 80\pi $;
②绕长方形的宽旋转时,圆柱的体积$ V=\pi×5^{2}×4=100\pi $,
因为$ 100\pi＞80\pi $,
所以该圆柱的最大体积为$ 100\pi $.

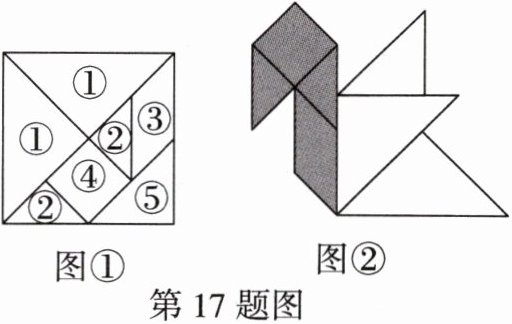
17. 数学文化情境 七巧板 古算书《周髀算经》中有关正方形的分割术,经过历代演变形成七巧板,如图①所示. 图②是由边长为8的正方形分割制作的七巧板拼摆成的图形. 请根据所学的七巧板知识回答下列问题：
(1)请用数字在图②中标出“纸鹤”的各个部分分别对应图①中七巧板的哪一块图形；
(2)求图②中阴影部分的面积；
(3)发挥你的想象力,用七巧板拼成一个图案,画出示意图,并标明所选板的编号.

答案：
解:
(1)标出各个部分如解图①所示;

(2)由题图可知,阴影部分的七巧板图形分别为1个正方形,1个平行四边形,2个小等腰直角三角形,
因为大正方形的边长是8,
所以$ S_{\text{大正方形}}=8×8 = 64 $,
所以$ S_{\text{阴影}}=2S_{\text{小三角形}}+S_{\text{正方形}}+S_{\text{平行四边形}} $
$=2×\frac{1}{16}×64+\frac{1}{8}×64+\frac{1}{8}×64 $
$=8 + 8+8=24 $;
(3)示意图如解图②所示(答案不唯一).