《2025年万唯中考情境题七年级数学上册苏科版》

8. 若关于$x的一元一次方程x - 4 = 3(x - m)的解为x = 1$,则$m$的值为(C)
A.-6
B.-2
C.2
D.6

答案： C

9.(教材习题第8题改编)欢欢在解方程$6(\frac{1}{2}x - 4) - 2x = a - (x - 1)$去括号时,等号右边括号里的-1没有变号,因而求得方程的解是$x = 6$,则方程正确的解是____x=7。

答案： x=7 【解析】把x=6代入3x-24-2x=a-x-1,得18-24-12=a-6-1,解得a=-11.故原方程为6($\frac{1}{2}$x-4)-2x=-11-(x-1),去括号,得3x-24-2x=-11-x+1.
移项,得3x-2x+x=24-11+1.合并同类项,得2x=14.
系数化为1,得x=7.

10.(教材习题第5题改编) 一题多变
变式1 已知两个方程同解,求参数的值
若关于$x的方程3x - 7 = 2(x + a)的解与方程4(1 - x) = x + 9$的解相同,则$a$的值为-4。
变式2 已知一个含参方程的解,求另一个含参方程的解
已知关于$x的一元一次方程2m + 9x = 3的解为x = 1$,则关于$x的方程2(2x + m) = 1 - 2x$的解为$x=\frac{7}{6}$。

答案： 变式1 -4 【解析】解方程4(1-x)=x+9,去括号,得4-4x=x+9.移项,得-4x-x=9-4.合并同类项,得-5x=5.两边同时除以-5,得x=-1.因为两方程的解相同,所以方程3x-7=2(x+a)的解为x=-1.将x=-1代入方程3x-7=2(x+a)中,得-3-7=2(-1+a),解得a=-4.
变式2 $x=\frac{7}{6}$ 【解析】将x=1代入方程2m+9x=3中,得2m+9=3.解得m=-3.将m=-3代入方程2(2x+m)=1-2x中,得2(2x-3)=1-2x.去括号,得4x-6=1-2x.移项,得4x+2x=1+6.合并同类项,得6x=7.系数化为1,得$x=\frac{7}{6}$.

11.(中考新考法·解题策略开放)下面是方程$3(x + 2) - (x + 2) = 6$的两种解法：
解法一：
$3x + 6 - x - 2 = 6$. ①
$2x + 4 = 6$. ②
$2x = 2$. ③
$x = 1$. ④
解法二：
$2(x + 2) = 6$. ①
$2x + 4 = 6$. ②
$2x = 2$. ③
$x = 1$. ④
(1)解法一中第①步的依据是去括号法则,解法二用到的数学思想是整体思想；
(2)选择一种你喜欢的解法解方程$5(x + 3) + 4 = 20 - 3(x + 3)$。
解：选择解法一：
去括号，得$5x + 15 + 4 = 20 - 3x - 9$.
移项，得$5x + 3x = 20 - 9 - 15 - 4$.
合并同类项，得$8x = -8$.
系数化为1，得$x = -1$.

答案： 解:
(1)去括号法则;整体思想;
(2)选择解法一:
去括号,得5x+15+4=20-3x-9.
移项,得5x+3x=20-9-15-4.
合并同类项,得8x=-8.
系数化为1,得x=-1.
选择解法二:
移项,得5(x+3)+3(x+3)=20-4.
合并同类项,得8(x+3)=16.
将(x+3)项的系数化为1,得x+3=2.
移项、合并同类项,得x=-1.
(任选一种解法作答即可)

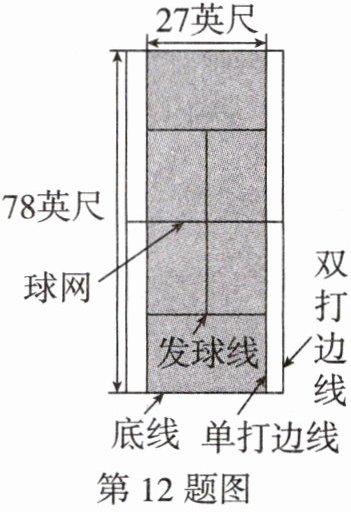
12.(黑白卷)随着近几年我国竞技网球在国际赛事上取得辉煌成绩,网球运动迅速普及。网球场分为单打区和双打区,其平面示意图如图所示(阴影区域为单打区),按照国际尺寸标准：单打区的长、宽分别为78英尺、27英尺,底线到发球线的长度与发球线到球网的长度比为$6:7$,单打边线到双打边线的宽度是底线到发球线的长度的$\frac{1}{4}$,求网球场双打区的宽度。

答案： 解:设底线到发球线的长度为6x英尺,
则发球线到球网的长度为7x英尺,
根据题意列方程,得2(6x+7x)=78,
解得x=3,
所以双打区的宽度为27+2×$\frac{1}{4}$×6×3=36(英尺),
答:网球场双打区的宽度为36英尺.

1. 解方程：(1)$|3x - 5| = 10$；
(2)$2|4x - 9| - 6 = 0$。

答案： 解:
(1)当3x-5＞0,则3x-5=10,
解得x=5,经检验,符合题意;
当3x-5＜0,则-(3x-5)=10,
解得$x=-\frac{5}{3}$,经检验,符合题意.
所以方程的解为x=5或$x=-\frac{5}{3}$;
(2)移项,得2|4x-9|=6.
绝对值整体系数化为1,得|4x-9|=3.
当4x-9＞0,则4x-9=3,
解得x=3,经检验,符合题意;
当4x-9＜0,则4x-9=-3,
解得$x=\frac{3}{2}$,经检验,符合题意.
所以方程的解为x=3或$x=\frac{3}{2}$.