《2025年万唯中考情境题七年级数学上册苏科版》

7. 选择一个运算符号填入算式$1+[\frac {2}{3}×6□(-2)^{3}]÷(-5)中的□$位置上,若要使计算结果最小,应填入的运算符号为(B)
A.+
B.-
C.×
D.÷

答案： B

8. 定义一种新的运算：$a※b= a^{2}÷(b-1)$,例如$3※5= 3^{2}÷(5-1)= 9÷4= \frac {9}{4}$,则计算$(-3)※4$的结果为3。

答案： 3 【解析】原式=(-3)²÷(4-1)=9÷3=3.

9. (教材复习题第14题改编)按照如图所示的运算程序,如果输入的数值是-3,则输出的值是$\frac{7}{54}$。

答案： $\frac{7}{54}$ 【解析】由题图可知，[(-3)²-1]×(-2)÷(-12)=8×(-2)÷(-12)=$\frac{4}{3}$，因为$\frac{4}{3}$＞1，所以[($\frac{4}{3}$)²-1]×(-2)÷(-12)=$\frac{7}{9}$×(-2)÷(-12)=$\frac{7}{54}$，因为$\frac{7}{54}$＜1，所以输出的值是$\frac{7}{54}$.

10. 用科学计算器进行计算的过程中,小明同学按$(1.4+0.6)×2x^{2}-2×5ab/c2= $的顺序输入,则计算器显示的正确答案是3。

答案： 3

11. 为锻炼身体,乐乐开始进行有氧运动——跑步,运动手环每2分钟记录乐乐的跑步动态,以300米为基准,下面是手环的记录情况(单位：米)：
+25,+10,+3,-5,-12,-7,+8。
(1)若乐乐平均跑1米消耗0.6卡路里能量,则这14分钟她消耗了多少能量？
(2)求这14分钟的平均跑步速度。(保留整数)

答案：
(1)由题意知，乐乐共跑了300×7+(25+10+3-5-12-7+8)=2122(米)，2122×0.6=1273.2(卡路里)，所以这14分钟她消耗了1273.2卡路里能量；
(2)由
(1)知，共跑了2122米，2122÷14≈152(米/分钟)，所以这14分钟的平均跑步速度约为152米/分钟.

12. (黑白卷改编)(中考新考法·阅读理解题)进位制是人们为了方便记数和运算而约定的记数系统,十进制是用0~9这十个数字满十进一,如$321= 3×10^{2}+2×10+1$,二进制则是用0和1这两个数字满二进一来表示数,如将二进制数10100转化为十进制数为$1×2^{4}+0×2^{3}+1×2^{2}+0×2+0= 20$。
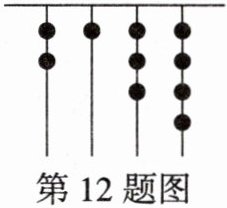
(1)将二进制数100110转化为十进制数为______38；
(2)将六进制数241转化为十进制数为______97；
(3)我国古代《易经》一书记载,远古时期,人们通过在绳子上打结来记录数量。如图,一位母亲在从右到左依次排列的绳子上打结,满5进1(五进制),用来记录孩子自出生后的天数,则这个孩子出生后的天数为多少？

由题图可知，这个五进制数为2134，将其化为十进制数为2×5³+1×5²+3×5+4=294，即这个孩子出生后的天数为294天.

答案：
(1)38；【解法提示】二进制数100110转化为十进制数为1×2⁵+0×2⁴+0×2³+1×2²+1×2+0=38.
(2)97；【解法提示】六进制数241转化为十进制数为2×6²+4×6+1=97.
(3)由题图可知，这个五进制数为2134，将其化为十进制数为2×5³+1×5²+3×5+4=294，即这个孩子出生后的天数为294天.