第15页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
10. 在0,2,-1,-2这四个数中,任意两个数相加,所得结果最小的是 (
A.0
B.-1
C.-2
D.-3
D
)A.0
B.-1
C.-2
D.-3
答案:
D
11. 如图,小明不慎将墨水滴在一条画好的数轴上,根据图中的数值,被墨水覆盖的所有整数之和是 (
A.-2
B.-1
C.1
D.2
B
)A.-2
B.-1
C.1
D.2
答案:
B
12. 数学文化情境 算筹 数学家刘徽在其著作《九章算术注》中,用不同颜色的算筹分别表示正数和负数,如图①表示的是(+4)+(-2)= 2的运算过程.按照这种方法,图②表示的算式是 (
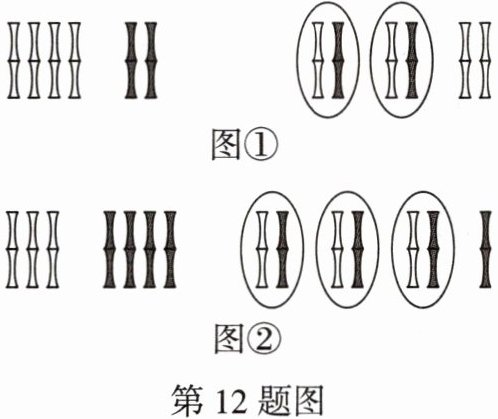
A.(-3)+(+4)= 1
B.(-3)+(-4)= -7
C.(+3)+(-4)= -1
D.(+3)+(+4)= 7
C
)
A.(-3)+(+4)= 1
B.(-3)+(-4)= -7
C.(+3)+(-4)= -1
D.(+3)+(+4)= 7
答案:
C 【解析】由题图①可得,白色小棍所表示的数为正数,黑色小棍所表示的数为负数,(+4)+(-2)=2,图②中有3根白色小棍和4根黑色小棍,所以图②所表示的算式是(+3)+(-4)=-1.
13. (中考新考法·阅读理解题)如图,定义在每一个枝干单元“$\begin{array}{c}a\\ b\quad c\end{array} $”中,都有a= b+c,则图中m+n+p= ______.
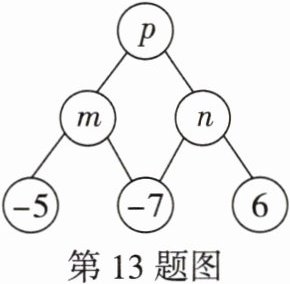


-26
答案:
-26 【解析】根据题意,得m=(-5)+(-7)=-12,n=(-7)+6=-1,所以p=m+n=(-12)+(-1)=-13,所以m+n+p=(-12)+(-1)+(-13)=-26.
14. 已知|a|= 2,|b|= 7,且a<b,则a+b的值为
9或5
.
答案:
9或5 【解析】因为|a|=2,所以a=2或a=-2,因为|b|=7,所以b=7或b=-7.因为a<b,所以a=2,b=7或a=-2,b=7,所以a+b的值是9或5.
15. (教材练习第3题改编)现有一副不含大小王的扑克牌,游戏规则如下:每人抽取相同数量的扑克牌,红色(红桃,方块)为正,黑色(黑桃,梅花)为负,数字之和结果大则获胜,小明、小鹏、小兰某次抽取的结果如下:(J为11,Q为12,K为13,A为1)
小明:红桃J,梅花4;
小鹏:方块3,红桃2;
小兰:黑桃K,方块5.
(1)请问三人中谁能获胜?
(2)若三人又各抽取一张牌,小明抽得黑桃7,小鹏抽得梅花A,小兰抽得红桃4,此时胜出者是谁?
小明:红桃J,梅花4;
小鹏:方块3,红桃2;
小兰:黑桃K,方块5.
(1)请问三人中谁能获胜?
(2)若三人又各抽取一张牌,小明抽得黑桃7,小鹏抽得梅花A,小兰抽得红桃4,此时胜出者是谁?
答案:
解:
(1)小明:(+11)+(-4)=11-4=7, 小鹏:(+3)+(+2)=5, 小兰:(-13)+(+5)=-(13-5)=-8, 因为7>5>-8,所以小明获胜;
(2)小明:7+(-7)=0, 小鹏:5+(-1)=4, 小兰:-8+(+4)=-4, 因为4>0>-4,所以此时胜出者是小鹏.
(1)小明:(+11)+(-4)=11-4=7, 小鹏:(+3)+(+2)=5, 小兰:(-13)+(+5)=-(13-5)=-8, 因为7>5>-8,所以小明获胜;
(2)小明:7+(-7)=0, 小鹏:5+(-1)=4, 小兰:-8+(+4)=-4, 因为4>0>-4,所以此时胜出者是小鹏.
16. 探索研究:
(1)比较下列各式的大小.(填“>”“<”或“=”)
①|3|+|5|
②|-2|+|6|
③$|-\dfrac{1}{2}|+|0|$
④$|-1|+|-\dfrac{3}{4}|$
(2)通过以上比较,请你分析、归纳出:两个数的绝对值之和
(1)比较下列各式的大小.(填“>”“<”或“=”)
①|3|+|5|
=
|3+5|,②|-2|+|6|
>
|-2+6|,③$|-\dfrac{1}{2}|+|0|$
=
$|-\dfrac{1}{2}+0|$,④$|-1|+|-\dfrac{3}{4}|$
=
$|-1+(-\dfrac{3}{4})|$;(2)通过以上比较,请你分析、归纳出:两个数的绝对值之和
大于或等于
两个数的和的绝对值.(填“大于”“小于”“大于或等于”“小于或等于”或“等于”)
答案:
(1)=,>,=,=;【解析】①因为|3|+|5|=8,|3+5|=8,所以|3|+|5|=|3+5|;②因为|-2|+|6|=8,|-2+6|=4,8>4,所以|-2|+|6|>|-2+6|;③因为|-$ \frac{1}{2} $|+|0|=$ \frac{1}{2} $,|-$ \frac{1}{2} $+0|=$ \frac{1}{2} $,所以|-$ \frac{1}{2} $|+|0|=|-$ \frac{1}{2} $+0|;④因为|-1|+|-$ \frac{3}{4} $|=$ \frac{7}{4} $,|-1+(-$ \frac{3}{4} $)|=$ \frac{7}{4} $,所以|-1|+|-$ \frac{3}{4} $|=|-1+(-$ \frac{3}{4} $)|.
(2)大于或等于 【解析】由
(1)得,当a,b同号时,|a|+|b|=|a+b|;当a=0或b=0时,|a|+|b|=|a+b|;当a,b异号时,|a|+|b|>|a+b|,所以两个数的绝对值之和大于或等于两个数的和的绝对值.
(1)=,>,=,=;【解析】①因为|3|+|5|=8,|3+5|=8,所以|3|+|5|=|3+5|;②因为|-2|+|6|=8,|-2+6|=4,8>4,所以|-2|+|6|>|-2+6|;③因为|-$ \frac{1}{2} $|+|0|=$ \frac{1}{2} $,|-$ \frac{1}{2} $+0|=$ \frac{1}{2} $,所以|-$ \frac{1}{2} $|+|0|=|-$ \frac{1}{2} $+0|;④因为|-1|+|-$ \frac{3}{4} $|=$ \frac{7}{4} $,|-1+(-$ \frac{3}{4} $)|=$ \frac{7}{4} $,所以|-1|+|-$ \frac{3}{4} $|=|-1+(-$ \frac{3}{4} $)|.
(2)大于或等于 【解析】由
(1)得,当a,b同号时,|a|+|b|=|a+b|;当a=0或b=0时,|a|+|b|=|a+b|;当a,b异号时,|a|+|b|>|a+b|,所以两个数的绝对值之和大于或等于两个数的和的绝对值.
查看更多完整答案,请扫码查看


