第69页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
8. (教材例4改编)已知一个等腰三角形。若其中一个角比另一个角的2倍小20°,这个等腰三角形顶角的度数是______
44°或80°
。
答案:
44°或80° 【解析】设其中一个角为x°,则另一个角为(2x-20)°,分情况讨论如下:①若x°的角为顶角,则x+2(2x-20)=180,解得x=44,②若x°的角为底角,则2x+(2x-20)=180,解得x=50,此时顶角的度数为2×50°-20°=80°,综上所述,这个等腰三角形顶角的度数为44°或80°.
9. (教材习题第13题改编)如图,将图①中的长方形剪开得到图②,图②中有4个长方形;将图②中的一个长方形剪开得到图③,图③中有7个长方形;将图③中的一个长方形剪开得到图④,图④中有10个长方形,请你根据这个裁剪规律,回答下列问题:
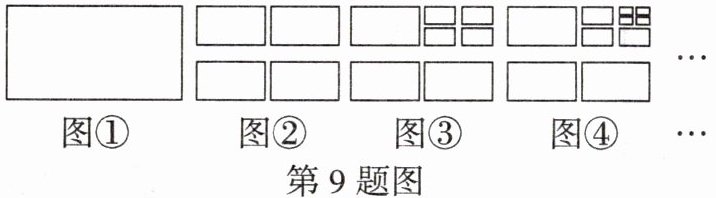
(1)图ⓝ有______个长方形;(用含n的代数式表示)
(2)按照此方式剪下去,第几个图形中有2026个长方形?
(3)已知图⑤中最小的长方形的周长为2,则图①中长方形的周长为多少?
(1)
(2)
(3)

(1)图ⓝ有______个长方形;(用含n的代数式表示)
(2)按照此方式剪下去,第几个图形中有2026个长方形?
(3)已知图⑤中最小的长方形的周长为2,则图①中长方形的周长为多少?
(1)
3n-2
(2)
676
(3)
32
答案:
(1)(3n-2);【解法提示】图①有1个长方形,图②有4个长方形,图③有7个长方形,图④有10个长方形,…,所以图ⓝ有(3n-2)个长方形.
(2)设根据题意,得3n-2=2026,解得n=676,所以第676个图形中有2026个长方形;
(3)设图①长方形的周长为a,则图②的最小的长方形周长为$\frac{1}{2}$a,图③中最小的长方形周长为$\frac{1}{4}$a=$\frac{1}{2^{3-1}}$a,所以图⑤的最小的长方形周长为$\frac{1}{2^{5-1}}$a=$\frac{1}{2^{4}}$a,所以$\frac{1}{2^{4}}$a=2,解得a=32,所以图①中长方形的周长为32.
(1)(3n-2);【解法提示】图①有1个长方形,图②有4个长方形,图③有7个长方形,图④有10个长方形,…,所以图ⓝ有(3n-2)个长方形.
(2)设根据题意,得3n-2=2026,解得n=676,所以第676个图形中有2026个长方形;
(3)设图①长方形的周长为a,则图②的最小的长方形周长为$\frac{1}{2}$a,图③中最小的长方形周长为$\frac{1}{4}$a=$\frac{1}{2^{3-1}}$a,所以图⑤的最小的长方形周长为$\frac{1}{2^{5-1}}$a=$\frac{1}{2^{4}}$a,所以$\frac{1}{2^{4}}$a=2,解得a=32,所以图①中长方形的周长为32.
10. (综合与实践·设计测量方案)【活动背景】在西安博物院展出过一件元代琉璃瓶(不规则形状),请你探究如何能测量出该琉璃瓶的底面积。
【活动准备】一个形似元代琉璃瓶的玻璃瓶(假设该玻璃瓶瓶身为圆柱),一个底面半径为8cm的圆柱形烧杯,一把直尺,一些水(水的损耗忽略不计)。
【活动探究】小智提出一种方案:
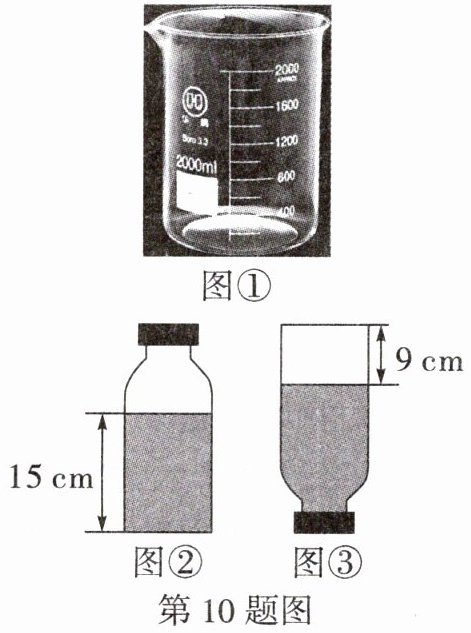
步骤一:先将玻璃瓶中装满水,再全部倒进如图①的圆柱形烧杯中,显示有1200mL(1mL= 1$cm^{3}$)的水;
步骤二:给玻璃瓶中装入一部分水,将瓶口密封。当玻璃瓶正放时,瓶内水面高度为15cm(如图②);
步骤三:将玻璃瓶倒放,此时瓶内空余部分的高度为9cm(如图③)。
【问题解决】(1)若根据步骤一操作,则此时烧杯中的水面高度大约为
(2)根据小智的步骤操作完,请你计算出玻璃瓶的底面积;
【问题拓展】(3)根据上述操作,你还能想出更多测量玻璃瓶底面积的方法吗?
【活动准备】一个形似元代琉璃瓶的玻璃瓶(假设该玻璃瓶瓶身为圆柱),一个底面半径为8cm的圆柱形烧杯,一把直尺,一些水(水的损耗忽略不计)。
【活动探究】小智提出一种方案:
步骤一:先将玻璃瓶中装满水,再全部倒进如图①的圆柱形烧杯中,显示有1200mL(1mL= 1$cm^{3}$)的水;
步骤二:给玻璃瓶中装入一部分水,将瓶口密封。当玻璃瓶正放时,瓶内水面高度为15cm(如图②);
步骤三:将玻璃瓶倒放,此时瓶内空余部分的高度为9cm(如图③)。

【问题解决】(1)若根据步骤一操作,则此时烧杯中的水面高度大约为
6.25
cm;(π取3)(2)根据小智的步骤操作完,请你计算出玻璃瓶的底面积;
设玻璃瓶的底面积为x cm²,根据题意,得15x=1200-9x,解得x=50,答:瓶子的底面积为50 cm²
【问题拓展】(3)根据上述操作,你还能想出更多测量玻璃瓶底面积的方法吗?
先将玻璃瓶中装满水,再将一部分水倒入烧杯得到这部分水的体积,后将瓶口密封并倒置,测得此时水面到瓶底的距离,然后用倒出的水的体积除以水面到瓶底的距离就能得到玻璃瓶底面积.(答案不唯一,合理即可)
答案:
(1)6.25;【解法提示】设烧杯中的水面高度大约为x cm,根据题意,得8×8πx=1200,解得x=6.25,所以烧杯中的水面高度大约为6.25 cm.
(2)设玻璃瓶的底面积为x cm²,根据题意,得15x=1200-9x,解得x=50,答:瓶子的底面积为50 cm²;
(3)先将玻璃瓶中装满水,再将一部分水倒入烧杯得到这部分水的体积,后将瓶口密封并倒置,测得此时水面到瓶底的距离,然后用倒出的水的体积除以水面到瓶底的距离就能得到玻璃瓶底面积.(答案不唯一,合理即可)
(1)6.25;【解法提示】设烧杯中的水面高度大约为x cm,根据题意,得8×8πx=1200,解得x=6.25,所以烧杯中的水面高度大约为6.25 cm.
(2)设玻璃瓶的底面积为x cm²,根据题意,得15x=1200-9x,解得x=50,答:瓶子的底面积为50 cm²;
(3)先将玻璃瓶中装满水,再将一部分水倒入烧杯得到这部分水的体积,后将瓶口密封并倒置,测得此时水面到瓶底的距离,然后用倒出的水的体积除以水面到瓶底的距离就能得到玻璃瓶底面积.(答案不唯一,合理即可)
查看更多完整答案,请扫码查看


