第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
9. $x + y - m - n$的相反数是 (
A.$x - y - m + n$
B.$-x + y + m - n$
C.$-x - y + m + n$
D.$x + y - m - n$
C
)A.$x - y - m + n$
B.$-x + y + m - n$
C.$-x - y + m + n$
D.$x + y - m - n$
答案:
C 【解析】x+y-m-n的相反数是-(x+y-m-n)=-x-y+m+n.
10. (黑白卷)若$2a - b = 1$,则代数式$8a - 4b + 2$的值为
6
.
答案:
6 【解析】8a-4b+2=4(2a-b)+2=4+2=6.
11. 传统文化情境 传统手工艺 刺绣是中国民间传统手工艺之一.如图是李阿姨的一幅刺绣作品,现要给这幅作品装裱一个边框并给边框上色,根据图中信息,上色部分(空白部分)的面积是
6.4a
$m^{2}$.(用含$a$的代数式表示)
答案:
6.4a 【解析】根据题意可得,上色部分的面积=大框的面积-作品的面积,即为2(a+a+0.6)-0.6(2-2a-2a)=6.4a(m²).
12. 先化简,再求值:$2(5x^{2} - 2x + 1) - 3(2x^{2} - x)$,其中$x = -2$.
答案:
解:原式=10x²-4x+2-6x²+3x=4x²-x+2.当x=-2时,原式=4×(-2)²-(-2)+2=20.
13. (教材探究改编)作差法是比较两个数大小的常用方法,例如:比较$-2和-5$的大小,因为$-2 - (-5) = -2 + 5 = 3 > 0$,所以$-2 > -5$.我们在学习整式的加减时,常常类比数的有关运算和运算律,数式具有通性,那么比较整式的大小时,同样也可以类比有理数比较大小的方法.
请根据以上材料,利用作差法解答下列问题:
(1)比较$2x + 5和2x + 7$的大小;
(2)比较$5x^{2} - 4x - 3和-\frac{1}{2}(8x + 12)$的大小.
请根据以上材料,利用作差法解答下列问题:
(1)比较$2x + 5和2x + 7$的大小;
(2)比较$5x^{2} - 4x - 3和-\frac{1}{2}(8x + 12)$的大小.
答案:
解:
(1)2x+5-(2x+7)=2x+5-2x-7=(2-2)x+(5-7)=-2.因为-2<0,所以2x+5<2x+7;
(2)5x²-4x-3-[-1/2(8x+12)]=5x²-4x-3-(-4x-6)=5x²-4x-3+4x+6=5x²+3.因为5x²+3>0,所以5x²-4x-3>-1/2(8x+12).
(1)2x+5-(2x+7)=2x+5-2x-7=(2-2)x+(5-7)=-2.因为-2<0,所以2x+5<2x+7;
(2)5x²-4x-3-[-1/2(8x+12)]=5x²-4x-3-(-4x-6)=5x²-4x-3+4x+6=5x²+3.因为5x²+3>0,所以5x²-4x-3>-1/2(8x+12).
14. (综合与实践·探究利用竖式进行整式运算)
【阅读理解】某数学兴趣小组在研究去括号、合并同类项时,合理利用了小学的列竖式进行加减运算的方法,如此一来不用去括号就能通过算式直接得出结果.具体做法如下:①将多项式按其中一个字母的降幂进行排列;②将同类项的系数写在对应的位置上;③求和(差)计算出对应位置上的系数;④写出结果.例如:计算$(-4x^{2} - 7 + 2x) - (1 - 2x + 3x^{2})$,令$A = -4x^{2} - 7 + 2x$,$B = 1 - 2x + 3x^{2}$,然后将两个整式按照$x$的降幂进行排列,$A = -4x^{2} + 2x - 7$,$B = 3x^{2} - 2x + 1$,将两式的系数对应列式如下:
$\begin{array}{r}-4\quad +2\quad -7\\ -+3\quad -2\quad +1\\ \hline -7\quad +4\quad -8\end{array} $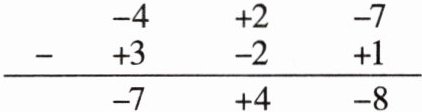
所以$(-4x^{2} - 7 + 2x) - (1 - 2x + 3x^{2}) = -7x^{2} + 4x - 8$.
【触类旁通】若$A = 5x^{2}y^{2} - 6x^{3}y + 7xy^{3} - 2x$,$B = 4x^{3}y - 3x^{2}y^{2} + x - 4xy^{3}$,请用“竖式法”求$A - 2B$.
(1)将$A$,$B按照y$的降幂进行排列;
(2)列出对应系数竖式;
(3)得出多项式的结果.
【阅读理解】某数学兴趣小组在研究去括号、合并同类项时,合理利用了小学的列竖式进行加减运算的方法,如此一来不用去括号就能通过算式直接得出结果.具体做法如下:①将多项式按其中一个字母的降幂进行排列;②将同类项的系数写在对应的位置上;③求和(差)计算出对应位置上的系数;④写出结果.例如:计算$(-4x^{2} - 7 + 2x) - (1 - 2x + 3x^{2})$,令$A = -4x^{2} - 7 + 2x$,$B = 1 - 2x + 3x^{2}$,然后将两个整式按照$x$的降幂进行排列,$A = -4x^{2} + 2x - 7$,$B = 3x^{2} - 2x + 1$,将两式的系数对应列式如下:
$\begin{array}{r}-4\quad +2\quad -7\\ -+3\quad -2\quad +1\\ \hline -7\quad +4\quad -8\end{array} $
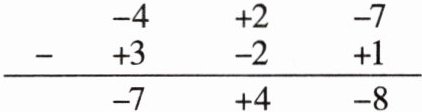
所以$(-4x^{2} - 7 + 2x) - (1 - 2x + 3x^{2}) = -7x^{2} + 4x - 8$.
【触类旁通】若$A = 5x^{2}y^{2} - 6x^{3}y + 7xy^{3} - 2x$,$B = 4x^{3}y - 3x^{2}y^{2} + x - 4xy^{3}$,请用“竖式法”求$A - 2B$.
(1)将$A$,$B按照y$的降幂进行排列;
(2)列出对应系数竖式;
(3)得出多项式的结果.
答案:
解:
(1)将A,B按照y的降幂进行排列:A=7xy³+5x²y²-6x³y-2x,B=-4xy³-3x²y²+4x³y+x;
(2)对应系数竖式为+7 +5 -6 -2- 2×(-4) 2×(-3) 2×(+4) 2×(+1)+15 +11 -14 -4
(3)得出多项式的结果为15xy³+11x²y²-14x³y-4x.
(1)将A,B按照y的降幂进行排列:A=7xy³+5x²y²-6x³y-2x,B=-4xy³-3x²y²+4x³y+x;
(2)对应系数竖式为+7 +5 -6 -2- 2×(-4) 2×(-3) 2×(+4) 2×(+1)+15 +11 -14 -4
(3)得出多项式的结果为15xy³+11x²y²-14x³y-4x.
查看更多完整答案,请扫码查看


