《2025年万唯中考情境题七年级数学上册苏科版》

9. 如图,下列给出的直线,射线,线段能相交的是(C)
A.a与b
B.b与d
C.b与c
D.c与d

答案： C

10. 同一平面内的四条直线最多有m个交点,最少有n个交点,则m-n的值为(D)
A.3
B.4
C.5
D.6

答案： D

11. 日常生活情境 商场布局优化 如图,某商场的四个主要入口位于点A,B,C,D处,现计划在商场内部增设一个智能导览机器人服务站,要求服务站的位置P到四个入口的距离之和最小,以便机器人能快速响应各入口顾客的需求。请画图确定服务站的最佳位置。

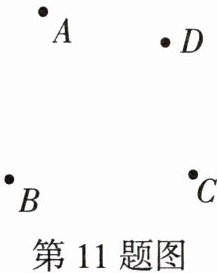
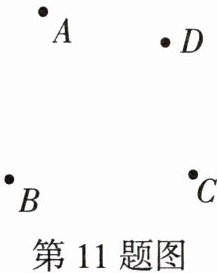
答案：
解:画图确定服务站点P的位置如解图所示.

12. 一题多设问 如图,数轴上的原点为O,点A,B分别为数轴上的两点。
(1)数轴是一条直线(填“直线”“射线”或“线段”)；
(2)数轴上点O左边的部分(包括点O)可以看作什么图形？怎么表示？
数轴上点O左边的部分(包括点O)可以看作是射线,可以表示成射线OA
(3)数轴上不小于-2且不大于3的部分可以看作什么图形,怎么表示？
数轴上不小于-2且不大于3的部分可以看作一条线段,可以表示成线段AB或线段BA
(4)以上三种图形之间有什么关系？
线段向一边延长可以形成射线,线段向两边延长可以形成直线

答案： 解:
(1)直线;
(2)数轴上点O左边的部分(包括点O)可以看作是射线,可以表示成射线OA;
(3)数轴上不小于-2且不大于3的部分可以看作一条线段,可以表示成线段AB或线段BA;
(4)线段向一边延长可以形成射线,线段向两边延长可以形成直线.

13. (教材复习题第3题改编)如图,在一条笔直的工业园区道路上,分别有甲、乙、丙三个工厂。甲工厂有60名员工,乙工厂有30名员工,丙工厂有20名员工。已知甲、乙两工厂相距200米,乙、丙两工厂相距300米。园区管理部门为了提升园区内员工生活的便利性,计划在这条道路上设置一个便利店,要使所有员工到便利店的路程总和最小,便利店应设置在(A)
A.甲工厂处
B.乙工厂处
C.甲、乙工厂之间
D.乙、丙工厂之间

答案： A 【解析】①在甲处设置便利店,所有员工的总路程=30×200+20×(200+300)=16 000(米);②在乙处设置便利店,所有员工的总路程=60×200+20×300=18 000(米);③在丙处设置便利店,所有员工的总路程=60×(200+300)+30×300=39 000(米);④当在甲、乙之间设置便利店时,设便利店到甲的距离是x(0＜x＜200),所有员工的总路程=60x+30×(200-x)+20×(300+200-x)=10x+16 000＞16 000;⑤当在乙、丙之间设置便利店时,设便利店到乙的距离是y(0＜y＜300),所有员工的总路程=60×(200+y)+30y+20×(300-y)=70y+18 000＞16 000;综上可得,便利店设置在甲工厂时,所有员工到便利店的路程总和最小.

14. (综合与实践·探究点数与可连线段数量规律)按要求作图,并回答问题：
(1)若平面内有三个不在同一直线上的点,将每两个点进行连接,可以连成几条线段？
(2)若平面内有四个点,且每三点都不在同一条直线上,将每两个点进行连接,可以连成几条线段？
(3)利用以上原理解决实际问题：在一场绘画展览中,有5个不同风格的主题展厅,主办方希望在每两个展厅之间互相设置一条单向的(即从一个展厅指向另一个展厅)参观引导路线,方便参观者按合理路线欣赏不同展厅作品,请问一共要设置多少条参观引导路线？
(4)写出一个可以用以上问题中的原理解决的实际问题。

答案：
解:
(1)如解图①,可以连成三条线段;
(2)如解图②,可以连成六条线段;

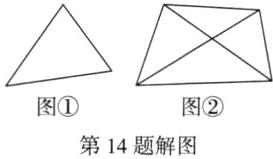
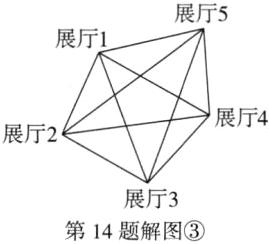
(3)如解图③,将5个展厅看作5个点,因为5个点可连成10条线段,所以每两个展厅之间的路线共有10条,又因为每两个展厅之间互相设置一条单向路线,所以共有2×10=20(条)单向引导路线;

(4)若将一个点看作一个篮球队,每个篮球队两两之间进行一场比赛,则三个篮球队共需进行三场比赛,四个篮球队共需进行六场比赛.(答案不唯一)