第99页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
9. 小颖家离学校1200m,其中一段为上坡路,另一段为下坡路,她去学校共用了16min,假设小颖上坡时的平均速度是3km/h,下坡时的平均速度是5km/h,则小颖上坡用了
4
min,下坡用了12
min.
答案:
4 12 解析:$16min = \frac{4}{15}h$,$1200m = 1.2km$.设上坡用了x h,则下坡用了$(\frac{4}{15} - x)h$.根据题意,得$3x + 5(\frac{4}{15} - x) = 1.2$,解得$x = \frac{1}{15}$,$\frac{4}{15} - x = \frac{1}{5}$,所以$\frac{1}{15}h = 4min$,$\frac{1}{5}h = 12min$,即上坡用了4 min,下坡用了12 min.
10. (绍兴中考)有两种消费券:A券,满60元减20元,B券,满90元减30元.即一次购物大于或等于60元、90元,付款时分别减20元、30元.小敏有一张A券,小聪有一张B券,他们都购买了一件标价相同的商品,各自付款,若能用券时用券,这样两人共付款150元,则所购商品的标价是____
100或85
元.
答案:
100或85 解析:设标价为x元,显然x不可能小于60.若$x≥90$,则两人均可用券,即$x - 20 + x - 30 = 150$,解得$x = 100$;若$60≤x < 90$,则只有小敏可用券,即$x - 20 + x = 150$,解得$x = 85$.所以所购商品的标价是100元或85元.
11. (2024·枣庄校级月考)某人在电车路轨旁与路轨平行的路上骑车行驶,他留意到每隔6min有一辆电车从他后面驶向前面,每隔2min有一辆电车从对面驶向后面.假设电车和此人行驶的速度都不变,请你根据示意图,推出电车每隔
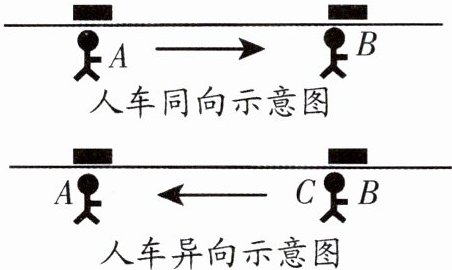
3
min从车站开出一辆.
答案:
3 解析:设电车发车时间间隔为x min,人骑车行驶6 min的路程,则电车行驶$(6 - x)min$,人骑车行驶2 min的路程,则电车行驶$(x - 2)min$,速度都是均匀的,所以可列方程$\frac{6 - x}{6} = \frac{x - 2}{2}$,解得$x = 3$.
12. 某电商销售A,B两种产品,相关信息如下表:
| | 进价/(元/件) | 售价/(元/件) |
| A产品 | 30 | 45 |
| B产品 | 40 | 60 |
(1)该电商十月份备货A,B两种产品一共用去31200元,其中A产品的数量比B产品数量的$\frac{1}{3}$多40件,A,B两种产品各备货多少件?
(2)该电商准备在十一月份的“双十一”活动中采取以下的优惠政策:A产品实行“买五免一”成组销售(每5件产品为一组,每买5件产品可以获得其中1件产品免费的优惠活动),B产品打八五折.
①A产品实行的“买五免一”的优惠活动相当于A产品每件打____
②若A,B两种产品均全部售完,则“双十一”期间这两种产品的总利润将比十月份增加5000元(十月份的备货在当月全部售完).该电商计划为“双十一”备货A产品500件,则B产品的备货数量是多少件?
(1)设B产品备货x件,因为A产品的数量比B产品数量的$\frac{1}{3}$多40件,所以A产品备货$(\frac{1}{3}x + 40)$件.因为该电商十月份备货两种产品一共用去31200元,所以$30(\frac{1}{3}x + 40) + 40x = 31200$,解得$x = 600$,所以$\frac{1}{3}x + 40 = 240$(件),所以A产品备货240件,B产品备货600件.
(2)②设“双十一”B产品的备货数量是y件,因为“双十一”A产品的备货数量是500件,所以“双十一”两种产品的利润为$[500×(45×0.8 - 30) + (60×0.85 - 40)y]$元.因为十月份两种产品的利润为$240×(45 - 30) + 600×(60 - 40) = 15600$(元),又因为“双十一”期间这两种产品的总利润将比十月份增加5000元,所以$500×(45×0.8 - 30) + (60×0.85 - 40)y - 5000 = 15600$,解得$y = 1600$,所以“双十一”B产品的备货数量是1600件.
| | 进价/(元/件) | 售价/(元/件) |
| A产品 | 30 | 45 |
| B产品 | 40 | 60 |
(1)该电商十月份备货A,B两种产品一共用去31200元,其中A产品的数量比B产品数量的$\frac{1}{3}$多40件,A,B两种产品各备货多少件?
(2)该电商准备在十一月份的“双十一”活动中采取以下的优惠政策:A产品实行“买五免一”成组销售(每5件产品为一组,每买5件产品可以获得其中1件产品免费的优惠活动),B产品打八五折.
①A产品实行的“买五免一”的优惠活动相当于A产品每件打____
八
____折;②若A,B两种产品均全部售完,则“双十一”期间这两种产品的总利润将比十月份增加5000元(十月份的备货在当月全部售完).该电商计划为“双十一”备货A产品500件,则B产品的备货数量是多少件?
(1)设B产品备货x件,因为A产品的数量比B产品数量的$\frac{1}{3}$多40件,所以A产品备货$(\frac{1}{3}x + 40)$件.因为该电商十月份备货两种产品一共用去31200元,所以$30(\frac{1}{3}x + 40) + 40x = 31200$,解得$x = 600$,所以$\frac{1}{3}x + 40 = 240$(件),所以A产品备货240件,B产品备货600件.
(2)②设“双十一”B产品的备货数量是y件,因为“双十一”A产品的备货数量是500件,所以“双十一”两种产品的利润为$[500×(45×0.8 - 30) + (60×0.85 - 40)y]$元.因为十月份两种产品的利润为$240×(45 - 30) + 600×(60 - 40) = 15600$(元),又因为“双十一”期间这两种产品的总利润将比十月份增加5000元,所以$500×(45×0.8 - 30) + (60×0.85 - 40)y - 5000 = 15600$,解得$y = 1600$,所以“双十一”B产品的备货数量是1600件.
答案:
(1)设B产品备货x件,因为A产品的数量比B产品数量的$\frac{1}{3}$多40件,所以A产品备货$(\frac{1}{3}x + 40)$件.因为该电商十月份备货两种产品一共用去31200元,所以$30(\frac{1}{3}x + 40) + 40x = 31200$,解得$x = 600$,所以$\frac{1}{3}x + 40 = 240$(件),所以A产品备货240件,B产品备货600件.
(2)①八②设“双十一”B产品的备货数量是y件,因为“双十一”A产品的备货数量是500件,所以“双十一”两种产品的利润为$[500×(45×0.8 - 30) + (60×0.85 - 40)y]$元.因为十月份两种产品的利润为$240×(45 - 30) + 600×(60 - 40) = 15600$(元),又因为“双十一”期间这两种产品的总利润将比十月份增加5000元,所以$500×(45×0.8 - 30) + (60×0.85 - 40)y - 5000 = 15600$,解得$y = 1600$,所以“双十一”B产品的备货数量是1600件.
(1)设B产品备货x件,因为A产品的数量比B产品数量的$\frac{1}{3}$多40件,所以A产品备货$(\frac{1}{3}x + 40)$件.因为该电商十月份备货两种产品一共用去31200元,所以$30(\frac{1}{3}x + 40) + 40x = 31200$,解得$x = 600$,所以$\frac{1}{3}x + 40 = 240$(件),所以A产品备货240件,B产品备货600件.
(2)①八②设“双十一”B产品的备货数量是y件,因为“双十一”A产品的备货数量是500件,所以“双十一”两种产品的利润为$[500×(45×0.8 - 30) + (60×0.85 - 40)y]$元.因为十月份两种产品的利润为$240×(45 - 30) + 600×(60 - 40) = 15600$(元),又因为“双十一”期间这两种产品的总利润将比十月份增加5000元,所以$500×(45×0.8 - 30) + (60×0.85 - 40)y - 5000 = 15600$,解得$y = 1600$,所以“双十一”B产品的备货数量是1600件.
13. (2024·德阳期中)甲、乙两船从B港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是50km/h,水流速度是a km/h,5h后两船同时分别到达A,C两港口,卸装货物后,又同时出发,甲船驶往C港口,乙船驶往A港口.(提示:顺水速度= 船速+水速;逆水速度= 船速-水速)
(1)A,C两港口相距多远?
(2)A,B港口间的距离比B,C港口间的距离比B,C港口间的距离多多少千米?(用含a的代数式表示)
(3)卸装货物后同时出发,两船又经过几小时相遇? 若相遇处距B港口50km,求甲船还需几小时到达C港口.

(1)A,C两港口相距多远?
(2)A,B港口间的距离比B,C港口间的距离比B,C港口间的距离多多少千米?(用含a的代数式表示)
(3)卸装货物后同时出发,两船又经过几小时相遇? 若相遇处距B港口50km,求甲船还需几小时到达C港口.

答案:
(1)因为两船在静水中的速度都是50 km/h,水流速度是a km/h,所以两船在行驶过程中的顺水速度都是$(50 + a)km/h$,逆水速度都是$(50 - a)km/h$.又因为甲、乙两船从B港口同时出发反向而行,5 h后两船同时分别到达A,C两港口,所以$AB = 5(50 + a) = (250 + 5a)km$,$BC = 5(50 - a) = (250 - 5a)km$,所以$AC = AB + BC = 250 + 5a + 250 - 5a = 500(km)$.答:A,C两港口相距500 km.
(2)由
(1)可知$AB = (250 + 5a)km$,$BC = (250 - 5a)km$,所以$AB - BC = 250 + 5a - (250 - 5a) = 10a(km)$.答:A,B港口间的距离比B,C港口间的距离多10a km.
(3)设卸装货物后同时出发,两船又经过x h相遇,则有$(50 + a)x + (50 - a)x = 500$,解得$x = 5$.相遇时,甲船逆水行驶,比开往A港口时的速度慢,故相遇时,在A,B两港口之间,设相遇在点D,作图如下: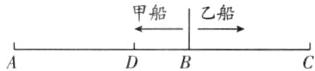 则有$AD = 5(50 - a) = (250 - 5a)km$,所以$BD = AB - AD = 250 + 5a - (250 - 5a) = 10a = 50$(km),解得$a = 5$,所以$CD = AC - AD = 500 - (250 - 5a) = 275(km)$,所以甲船到达C港口还需时间为$\frac{CD}{v_{逆水}} = \frac{275}{50 - 5} = \frac{55}{9}(h)$.答:卸装货物后同时出发,两船又经过5 h相遇.若相遇处距B港口50 km,甲船还需$\frac{55}{9}h$到达C港口.
则有$AD = 5(50 - a) = (250 - 5a)km$,所以$BD = AB - AD = 250 + 5a - (250 - 5a) = 10a = 50$(km),解得$a = 5$,所以$CD = AC - AD = 500 - (250 - 5a) = 275(km)$,所以甲船到达C港口还需时间为$\frac{CD}{v_{逆水}} = \frac{275}{50 - 5} = \frac{55}{9}(h)$.答:卸装货物后同时出发,两船又经过5 h相遇.若相遇处距B港口50 km,甲船还需$\frac{55}{9}h$到达C港口.
(1)因为两船在静水中的速度都是50 km/h,水流速度是a km/h,所以两船在行驶过程中的顺水速度都是$(50 + a)km/h$,逆水速度都是$(50 - a)km/h$.又因为甲、乙两船从B港口同时出发反向而行,5 h后两船同时分别到达A,C两港口,所以$AB = 5(50 + a) = (250 + 5a)km$,$BC = 5(50 - a) = (250 - 5a)km$,所以$AC = AB + BC = 250 + 5a + 250 - 5a = 500(km)$.答:A,C两港口相距500 km.
(2)由
(1)可知$AB = (250 + 5a)km$,$BC = (250 - 5a)km$,所以$AB - BC = 250 + 5a - (250 - 5a) = 10a(km)$.答:A,B港口间的距离比B,C港口间的距离多10a km.
(3)设卸装货物后同时出发,两船又经过x h相遇,则有$(50 + a)x + (50 - a)x = 500$,解得$x = 5$.相遇时,甲船逆水行驶,比开往A港口时的速度慢,故相遇时,在A,B两港口之间,设相遇在点D,作图如下:
 则有$AD = 5(50 - a) = (250 - 5a)km$,所以$BD = AB - AD = 250 + 5a - (250 - 5a) = 10a = 50$(km),解得$a = 5$,所以$CD = AC - AD = 500 - (250 - 5a) = 275(km)$,所以甲船到达C港口还需时间为$\frac{CD}{v_{逆水}} = \frac{275}{50 - 5} = \frac{55}{9}(h)$.答:卸装货物后同时出发,两船又经过5 h相遇.若相遇处距B港口50 km,甲船还需$\frac{55}{9}h$到达C港口.
则有$AD = 5(50 - a) = (250 - 5a)km$,所以$BD = AB - AD = 250 + 5a - (250 - 5a) = 10a = 50$(km),解得$a = 5$,所以$CD = AC - AD = 500 - (250 - 5a) = 275(km)$,所以甲船到达C港口还需时间为$\frac{CD}{v_{逆水}} = \frac{275}{50 - 5} = \frac{55}{9}(h)$.答:卸装货物后同时出发,两船又经过5 h相遇.若相遇处距B港口50 km,甲船还需$\frac{55}{9}h$到达C港口. 查看更多完整答案,请扫码查看


