《2025年学霸题中题七年级数学上册苏科版》

1. 已知数a,b,c在数轴上的位置如图所示,比较a,b,c,-a,-b,|c|,0的大小,并用“＜”号将它们连接起来.

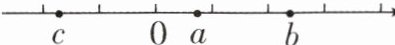
答案： 在数轴上标出 -a,-b,|c|,可知 -b ＜ c ＜ -a ＜ 0 ＜ a ＜ |c| ＜ b.

2. 比较$-\frac {10}{13},-\frac {8}{9}$的大小.

答案： 因为 $-\frac{10}{13}-(-\frac{8}{9})=-\frac{10}{13}+\frac{8}{9}=-\frac{90}{117}+\frac{104}{117}=\frac{14}{117}＞0$,所以 $-\frac{10}{13}＞-\frac{8}{9}$.

3. 若$x= -\frac {2022×2023}{2024×2025},y= -\frac {2022×2024}{2023×2025},z= -\frac {2022×2025}{2023×2024}$,比较x,y,z的大小.

答案： $\frac{x}{y}=-\frac{2022×2023}{2024×2025}×(-\frac{2023×2025}{2022×2024})=\frac{2023^{2}}{2024^{2}}＜1$,又因为 x,y 均为负数,所以 $x ＞ y$,同理,$\frac{y}{z}=\frac{2024^{2}}{2025^{2}}＜1$,可得 $y ＞ z$,所以 $x ＞ y ＞ z$.

4. 比较$\frac {1012}{2025}与\frac {1014}{2027}$的大小.

答案： 因为 $\frac{1012}{2025}＜\frac{1}{2}$ 且 $\frac{1}{2}＜\frac{1014}{2027}$,所以 $\frac{1012}{2025}＜\frac{1014}{2027}$.

5. 比较$-\frac {6}{23},-\frac {4}{17},-\frac {3}{11},-\frac {12}{47}$四个数的大小.

答案： 通分使得分数的分子都为 12,即 $-\frac{6}{23}=-\frac{12}{46},-\frac{4}{17}=-\frac{12}{51},-\frac{3}{11}=-\frac{12}{44},-\frac{12}{47}=-\frac{12}{47}$,因为 $-\frac{12}{44}＜-\frac{12}{46}＜-\frac{12}{47}＜-\frac{12}{51}$,所以 $-\frac{3}{11}＜-\frac{6}{23}＜-\frac{12}{47}＜-\frac{4}{17}$.

6. 比较$\frac {5551}{5555},\frac {9215}{9219}$的大小.

答案： $\frac{5551}{5555}$ 的倒数是 $1\frac{4}{5551},\frac{9215}{9219}$ 的倒数是 $1\frac{4}{9215}$,因为 $1\frac{4}{5551}＞1\frac{4}{9215}$,所以 $\frac{5551}{5555}＜\frac{9215}{9219}$.

7. 设$a= \frac {19961995}{1995},b= \frac {19951996}{1996},c= \frac {19951996}{1995},d= \frac {19961995}{1996}$,比较a,b,c,d的大小.

答案： 各数进行裂项,即 $a=\frac{19951995 + 10000}{1995}=10001+\frac{10000}{1995},b=\frac{19961996 - 10000}{1996}=10001-\frac{10000}{1996},c=\frac{19951995 + 1}{1995}=10001+\frac{1}{1995},d=\frac{19961996 - 1}{1996}=10001-\frac{1}{1996}$,因为 $\frac{10000}{1995}＞\frac{1}{1995}＞-\frac{1}{1996}＞-\frac{10000}{1996}$,所以 $a ＞ c ＞ d ＞ b$.

8. 已知a,b是有理数,且a,b异号,则$|a+b|,|a-b|,|a|+|b|$的大小关系为$|a + b|＜|a - b|=|a|+|b|$.

答案： $|a + b|＜|a - b|=|a|+|b|$ 解析:已知 a,b 异号,不妨取 $a = 2,b = - 1$ 或 $a = - 1,b = 2$.当 $a = 2,b = - 1$ 时,$|a + b|=|2+( - 1)|=1,|a - b|=|2-( - 1)|=3,|a|+|b|=|2|+| - 1|=3$;当 $a = - 1,b = 2$ 时,$|a + b|=| - 1 + 2|=1,|a - b|=| - 1 - 2|=3,|a|+|b|=| - 1|+|2|=3$,所以 $|a + b|＜|a - b|=|a|+|b|$.