《2025年学霸题中题七年级数学上册苏科版》

9. 如图,一个瓶子的容积为 1 L,瓶内装着一些溶液.当瓶子正放时,瓶内溶液的高度为 30 cm,当瓶子倒放时,空余部分的高度为 10 cm.现将瓶内的溶液全部倒入一个圆柱形的杯子里,杯内溶液的高度为 15 cm,则圆柱形杯子的内底面半径约为 (B)
A.2.8 cm
B.4.0 cm
C.5.0 cm
D.6.2 cm

答案： B 解析:设溶液的体积为 x L,那么空余部分的体积为 $\frac{1}{3}x$ L,由题意得 $x + \frac{1}{3}x = 1$，解得 $x = 0.75$.设圆柱形杯子的内底面半径约为 a cm,则 $15πa^{2} = 0.75×1000$，解得 $a ≈ 4.0$，所以圆柱形杯子的内底面半径约为 4.0 cm,故选 B.

10. 轮船在顺水中的速度为 28 km/h,在逆水中的速度为 24 km/h,水面上一漂浮物顺水漂流 20 km,则它漂浮了10h.

答案： 10 解析:设轮船在静水中的速度为 x km/h.由题意得 $2x = 28 + 24$，解得 $x = 26$，即轮船在静水中的速度为 26 km/h,水流速度为 $28 - 26 = 2(km/h)$，所以该漂浮物漂浮时间为 $\frac{20}{2} = 10(h)$.

11. 一个五位数最高位上的数字是 2,如果把这个数字移到个位数字的右边,那么所得的数比原来的数的 3 倍多 489,求原数.

答案： 设原数的后四位是 x,则原数是 $20000 + x$，移后的数是 $10x + 2$.由题意得 $10x + 2 = 3(20000 + x) + 489$，解得 $x = 8641$，故原数为 28 641.

12. 某商品月末的进货价比月初的进货价降了 8%,而销售价不变,这样,利润率月末比月初高 10%,则月初的利润率是15%.

答案： 15% 解析:设月初的利润率为 x%,月初的进货价为 M,则 0.92M 是该商品月末的进货价,可得 $M(1 + x\%) = 0.92M[1 + (x + 10)\%]$，约去 M 得 $1 + x\% = 0.92[1 + (x + 10)\%]$，解得 $x = 15$.故月初的利润率为 15%.

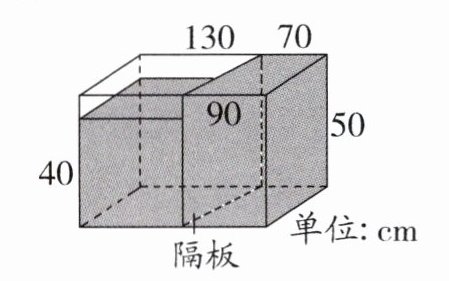
13. 如图,水平桌面上有个内部装水的长方体箱子,箱内有一个与底面垂直的隔板,且隔板左右两侧的水面高度分别为 40 cm、50 cm,现将隔板抽出,若过程中箱内的水量未改变,且不计箱子及隔板厚度,则根据图中的数据,隔板抽出后水面静止时,箱内的水面高度为44cm.

答案： 44 解析:设长方体的宽为 x cm,抽出隔板后水面高度为 h cm,长方体的长为 $130 + 70 = 200(cm)$，$200 - 90 = 110(cm)$，根据题意得 $\frac{(130 + 110)x}{2}×40 + \frac{(70 + 90)x}{2}×50 = 200$ $x$ $h$，解得 $h = 44$.所以隔板抽出后水面静止时,箱内的水面高度为 44 cm.

14. 七(1)班全体同学进行了一次转盘得分活动.如图,将转盘等分成 8 格,每人转动一次,指针指向的数字就是获得的得分,指针落在边界则重新转动一次.根据小红、小明两位同学的对话,求七(1)班共有学生多少人.

答案： 设得 3 分,4 分,5 分和 6 分的共有 x 人,他们平均得分为 y 分.由条件得:
(1)得分不足 7 分的人平均得分为 3 分,依题意得 $xy + 3×2 + 5×1 = 3(x + 5 + 3)$，整理得 $xy - 3x = 13$ ①.
(2)得 3 分及以上的人平均得分为 4.5 分,依题意得 $xy + 3×7 + 4×8 = 4.5(x + 3 + 4)$，整理得 $4.5x - xy = 21.5$ ②.由①+②得 $xy - 3x + 4.5x - xy = 13 + 21.5$，解得 $x = 23$.故七
(1)班共有学生 $23 + 5 + 3 + 4 = 38$(人).