《2025年学霸题中题七年级数学上册苏科版》

1. 将一张长方形纸对折,然后用笔尖在上面扎出“M”,再把它铺平,你见到的图形可能是(A)

答案： A

2. 某数学小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是 (D)
A.甲种方案所用铁丝最长
B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长
D.三种方案所用铁丝一样长

答案： D

3. (2025·甘肃期末)如图,将一个半径为 1 的圆形纸片连续对折三次之后,用剪刀沿虚线①剪开,可以得到一个三角形,内角和为 $ 180 ^ { \circ } $,则将该三角形展开后得到的多边形的内角和为 (C)
A.$ 180 ^ { \circ } $
B.$ 540 ^ { \circ } $
C.$ 1080 ^ { \circ } $
D.$ 2160 ^ { \circ } $

答案： C 解析：因为对折三次之后沿虚线剪开可以得到一个三角形，三角形内角和为 $180^{\circ}$，所以将该三角形展开后得到的多边形的内角和为 $180^{\circ} × 8 - 360^{\circ} = 1080^{\circ}$，故选 C。

4. 如图,观察月历,2025 年的国庆节是星期三.

答案： 三 解析：根据 2025 年 6 月的月历知 7 月 1 日为星期二，7 月 1 日到国庆节还有 92 天，因为 $92 ÷ 7 = 13$（个）$\cdots\cdots1$（天），所以 2025 年国庆节是星期三。

5. (1)有一块三角形的空地如图①所示,为了美化环境,现计划在以三角形各顶点为圆心,2m 长为半径的扇形区域(阴影部分)种上花草,那么种上花草的扇形区域总面积是______ $ m ^ { 2 } $.

(2)如图②,现需在一块四边形的空地上建造一个花园,要在以花园的四个顶点为圆心,2m 长为半径的扇形区域(阴影部分)种上花草,则种上花草的区域(阴影部分)的总面积是______ $ m ^ { 2 } $.

答案：

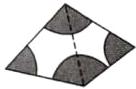
(1) $2\pi$ 解析：因为三个扇形的圆心角的和为 $180^{\circ}$，所以 $S_{\text{阴影部分}} = \pi × 2^{2} × \frac{180^{\circ}}{360^{\circ}} = 2\pi$。
(2) $4\pi$ 解析：如图，将四边形沿虚线剪裁成 2 个三角形，所以原四个扇形就被分成 6 个扇形。所以以花园的四个顶点为圆心，2m 长为半径的扇形区域恰好能拼成一个完整的圆，所以 $S_{\text{阴影部分}} = \pi \cdot r^{2} = \pi \cdot 2^{2} = 4\pi(\text{m}^{2})$。

6. 观察如图所示的月历,解答下列问题：

(1)用长方形框去框月历里同一行的 4 个连续的数.若框里 4 个数的和是 66,则这 4 个数分别是多少?
(2)用一个 $ 4 × 3 $ 的长方形框去任意框 12 个数(如图),框里的 12 个数的和能等于 222 吗?能等于 246 吗?若能,请求出框里的 12 个数中的最小数；若不能,请说明理由.

答案：
(1) 令框里 4 个数中的最小数为 $x$，由题意得 $4x + 6 = 66$，解得 $x = 15$。所以其他三个数为 16，17，18，所以这 4 个数分别是 15，16，17，18。
(2) 令第一行的第一个数即最小的数是 $x$，则其他 11 个数分别为 $x + 1$，$x + 2$，$x + 3$，$x + 7$，$x + 8$，$x + 9$，$x + 10$，$x + 14$，$x + 15$，$x + 16$，$x + 17$，这 12 个数的和为 $x + (x + 1) + (x + 2) + (x + 3) + (x + 7) + (x + 8) + (x + 9) + (x + 10) + (x + 14) + (x + 15) + (x + 16) + (x + 17) = 12x + 102$。 当和为 222 时，$12x + 102 = 222$，解得 $x = 10$。此时，最小的数为 10。观察月历，能框出 12 个数的和等于 222。 当和为 246 时，$12x + 102 = 246$，解得 $x = 12$，此时，最小的数为 12。观察月历，不能框出 12 个数的和等于 246。