《2025年学霸题中题七年级数学上册苏科版》

8. 若$|6 - x|与|y + 9|$互为相反数,则$x = $6,$y = $-9.

答案： 6 -9

9. (1)当$x = $3时,$|x - 3| + 5$有最小值,为5.
(2)当$x = $$-\frac{1}{2}$时,$9 - |x + \frac{1}{2}|$有最大值,为9.

答案：
(1)3 5
(2)$-\frac{1}{2}$ 9

10. 已知$|xy - 2|与|y - 1|$互为相反数,试求$\frac{1}{xy} + \frac{1}{(x + 1)(y + 1)} + \frac{1}{(x + 2)(y + 2)} + … + \frac{1}{(x + 2025)(y + 2025)}$的值.

答案： 由题意得$|xy - 2| + |y - 1| = 0$,所以$xy = 2$,$y = 1$,所以$x = 2$,则原式=$\frac{1}{1×2} + \frac{1}{2×3} + \frac{1}{3×4} + \cdots + \frac{1}{2026×2027} = 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + \cdots + \frac{1}{2026} - \frac{1}{2027} = 1 - \frac{1}{2027} = \frac{2026}{2027}$.

11. (2025·武汉校级月考)【定义新知】
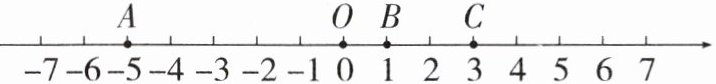
我们知道:式子$|x - 3|$的几何意义是数轴上表示有理数x的点与表示有理数3的点之间的距离,因此,若点A,B在数轴上分别表示有理数a,b,则A,B两点之间的距离$AB = |a - b|$.若点P表示的数为x,请根据数轴解决以下问题:
(1)若$|x + 5| = 6$,则x的值为1或-11.
(2)当$|x + 3| + |x - 1|$取最小值时,x可以取整数-3,-2,-1,0,1;$|x + 3| - |x - 1|$的最大值为4.
(3)当$x = $-2时,$|x + 2| + |x + 6| + |x - 1|$的值最小,最小值为7.
(4)如图,一条笔直的公路边有三个居民区A,B,C和市民广场O,居民区A,B,C分别位于市民广场左侧5km,右侧1km,右侧3km.A居民区有居民1000人,B居民区有居民2000人,C居民区有居民3000人.现因物流需要,需要在该公路上建菜鸟驿站,用于接收这3个小区的快递,若快递的运输成本为1元/(千份·千米),那么菜鸟驿站建在何处才能使总运输成本最低,最低成本是多少?

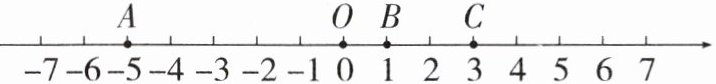
建在C居民区（3km处），最低成本12000元。

答案：
(1) $|x + 5| = 6$表示数轴上点$x$与$-5$的距离为$6$，则$x + 5 = 6$或$x + 5=-6$，解得$x = 1$或$x=-11$。
(2) $|x + 3| + |x - 1|$表示点$x$到$-3$和$1$的距离之和，当$-3\leqslant x\leqslant1$时，距离之和最小，此时$x$可取整数$-3,-2,-1,0,1$；$|x + 3| - |x - 1|$，当$x\geqslant1$时，原式$=(x + 3)-(x - 1)=4$，为最大值。
(3) $|x + 2| + |x + 6| + |x - 1|$表示点$x$到$-6,-2,1$的距离之和，当$x=-2$时，距离之和最小，最小值为$|-2 + 6| + |-2 - 1|=4 + 3=7$。
(4) 设驿站在数轴上表示的数为$x$，总成本$y=1000|x + 5| + 2000|x - 1| + 3000|x - 3|$（单位：元）。当$x = 3$时，$y=1000×8 + 2000×2 + 3000×0=8000 + 4000=12000$元，此时成本最低。
(1) $1$或$-11$
(2) $-3,-2,-1,0,1$；$4$
(3) $-2$；$7$
(4) 建在$C$居民区（$3km$处），最低成本$12000$元。