《2025年学霸题中题七年级数学上册苏科版》

8. 图中以点A,B,C,D,E,O为端点的不同线段有 (C)
A.8条
B.10条
C.13条
D.15条

答案： C 解析:共有13条不同的线段,分别是线段AB,AC,BC,AE,EC,CD,BD,BO,OE,BE,AO,AD,OD.故选C.

9. 在两条平行的直线m,n上分别有4个点和5个点,任选这9个点中的两个连一条直线,则一共可以得到不同的直线的条数为______22.

答案： 22 解析:任选两点都在m(或n)上,只能连出直线m(或n);若任选两点分别在m,n上,则可连直线4×5=20(条),所以一共可以连22条直线.

10. (2025·廊坊期末)一个棋盘上有黑、白两色棋子若干,若把颜色相同的三颗棋子在同一条直线上看作一条直线.请你根据图示,判断满足这种条件的直线共有______条.

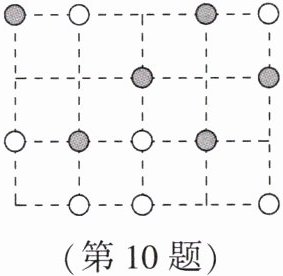
答案：
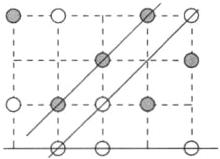
3 解析:如图所示,满足条件的直线共有3条.

11. (1)如图①,A,B两个村庄在一条河l(不计河的宽度)的两侧,现要在河上建一座码头,使它到A,B两个村庄的距离之和最小? 请你确定码头的位置,在图中用点C表示出来,并说明理由.
(2)如图②,草原上有四口油井,位于四边形ABCD的四个顶点上,现在要建立一个维修站H,试问H建在何处,才能使它到四口油井的距离之和HA+HB+HC+HD最小? 说明理由.

答案：

(1)应建在AB连线与l的交点处.如图①,连接AB,交l于点C,则点C就是码头的位置.理由:两点之间线段最短.
(2)应建在AC,BD连线的交点处.如图②,连接AC,BD,交点为H,则点H即为维修站的位置.理由:两点之间线段最短,连接AC,BD,路程最短,在两线段的交点处建维修站才能使得HA+HB+HC+HD最小.

12. 探究归纳题:


(1)试验分析:
如图①,直线上有两点A与B,图中有线段1条.
(2)拓展延伸:
如图②,直线上有A,B,C三个点,以A为端点,有线段AB、线段AC;同样以C为端点,有线段CA、线段CB;以B为端点,有线段BA、线段BC,去除重复线段,图②共有3条线段.同样方法探究出图③中有6条线段.
(3)探索归纳:
如果直线上有n(n为正整数)个点,那么共有$\frac{n(n - 1)}{2}$条线段.(用含n的式子表示)
(4)解决问题:
公共汽车往返于A,B两地之间,中途有4个停靠点(共6个站点),若相邻各站之间距离互不相等,则需要多少种车票? 有多少种票价?
请将这个问题转化为上述模型,并应用上述模型的结论解决问题.
6个站点可对应为直线上的6个点,由(3)得共有$\frac{6×5}{2}=15$(条)线段,又因为各站之间距离互不相等,所以有15种不同的票价.两地之间有往返两种车票,所以共有15×2=30(种)车票.

答案：
(1)1
(2)3 6
(3)$\frac{n(n - 1)}{2}$
(4)6个站点可对应为直线上的6个点,由
(3)得共有$\frac{6×5}{2}=15$(条)线段,又因为各站之间距离互不相等,所以有15种不同的票价.两地之间有往返两种车票,所以共有15×2=30(种)车票.

13. (1)如图,2条直线相交只有1个交点,3条直线相交最多有3个交点,4条直线相交最多有6个交点,5条直线相交最多有10个交点,6条直线相交最多有15个交点,n条直线相交最多有$\frac{n(n - 1)}{2}$个交点.

(2)平面上不重合的两点确定一条直线,不同三点最多可确定3条直线,若平面上不同的n个点最多能确定45条直线,则n的值为10.

答案：
(1)15 $\frac{n(n - 1)}{2}$ 解析:6条直线相交最多有10+5=15(个)交点;n条直线相交最多有1+2+3+…+(n - 1)=$\frac{n(n - 1)}{2}$个交点.
(2)10