《2025年学霸题中题七年级数学上册苏科版》

11. (1)某冷冻厂的冷库温度是$-4^{\circ }C$,现有一批食品必须在$-28^{\circ }C$及以下冷藏,如果每小时能降温$6^{\circ }C$,那么至少应等待4h才能放入该食品.
(2)一辆汽车5h行了320km,照这样计算,行960km要15h.

答案：
(1) $4$ 解析：由题意，得 $[-4 - (-28)] ÷ 6 = 4$ (h)。
(2) $15$ 解析：每小时行 $320 ÷ 5 = 64$ (km)，所以行 $960$ km 要用 $960 ÷ 64 = 15$ (h)。

12. (2025·六安期中)定义新运算：我们把2÷2÷2写作2^{③},(-3)÷(-3)÷(-3)÷(-3)写作$(-3)^{\enclose{circle} {4}},$一般地,把$\underbrace {a÷a÷a÷... ÷a}_{n个a}(a≠0)$记作$a^{\enclose{circle} {n}}.$通过以上信息,请计算：$2025^{②}×(-\frac {1}{2})^{\enclose{circle} {4}}+(-1)^{\enclose{circle} {17}}= $3.

答案：
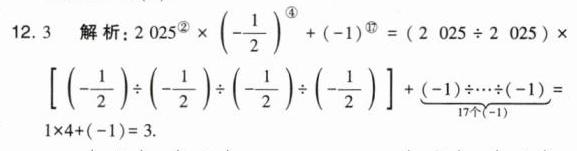
$3$ 

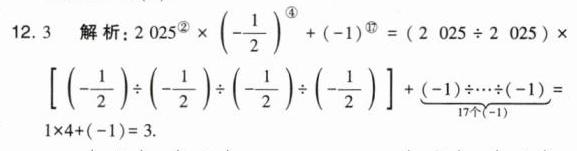
13. 计算：
(1)$(-\frac {2}{3})÷(-\frac {8}{5})÷(-0.25)×(-3)$；
(2)$-8÷[(-\frac {3}{8})×\frac {3}{8}]÷(-10\frac {2}{3})$；
(3)$(-5)÷(-1\frac {2}{7})×\frac {4}{5}×(-2\frac {1}{4})÷7$.

答案：
(1) $(-\frac{2}{3}) ÷ (-\frac{8}{5}) ÷ (-0.25) × (-3) = (-\frac{2}{3}) × (-\frac{5}{8}) × (-4) × (-3) = [(-\frac{2}{3}) × (-3)] × [(-\frac{5}{8}) × (-4)] = 2 × \frac{5}{2} = 5$。
(2) $-8 ÷ [(-\frac{3}{8}) × \frac{3}{8}] ÷ (-10\frac{2}{3}) = -8 ÷ (-\frac{9}{64}) ÷ (-\frac{32}{3}) = -8 × (-\frac{64}{9}) × (-\frac{3}{32}) = -\frac{16}{3}$。
(3) $(-5) ÷ (-1\frac{2}{7}) × \frac{4}{5} × (-2\frac{1}{4}) ÷ 7 = (-5) × (-\frac{7}{9}) × \frac{4}{5} × (-\frac{9}{4}) × \frac{1}{7} = (-5) × \frac{4}{5} × [(-\frac{7}{9}) × (-\frac{9}{4})] × \frac{1}{7} = -4 × \frac{7}{4} × \frac{1}{7} = -1$。

14. 阅读下列材料：
计算：$\frac {1}{24}÷(\frac {1}{3}-\frac {1}{4}+\frac {1}{12})$.
解法一：原式$=\frac {1}{24}÷\frac {1}{3}-\frac {1}{24}÷\frac {1}{4}+\frac {1}{24}÷\frac {1}{12}= \frac {11}{24}$.
解法二：原式的倒数$=(\frac {1}{3}-\frac {1}{4}+\frac {1}{12})÷\frac {1}{24}= (\frac {1}{3}-\frac {1}{4}+\frac {1}{12})×24= \frac {1}{3}×24-\frac {1}{4}×24+\frac {1}{12}×24= 4$,
所以原式$=\frac {1}{4}$.
(1)上述得到的结果不同,你认为解法一是错误的；
(2)请你选择合适的解法计算：$(-\frac {1}{42})÷(\frac {1}{6}-\frac {3}{14}+\frac {2}{3}-\frac {2}{7})$.
原式的倒数$=(\frac{1}{6}-\frac{3}{14}+\frac{2}{3}-\frac{2}{7})÷(-\frac{1}{42})=(\frac{1}{6}-\frac{3}{14}+\frac{2}{3}-\frac{2}{7})×(-42)=-7 + 9 - 28 + 12=-14$，所以原式$=-\frac{1}{14}$。

答案：
(1) 一
(2) 原式的倒数 $= (\frac{1}{6} - \frac{3}{14} + \frac{2}{3} - \frac{2}{7}) ÷ (-\frac{1}{42}) = (\frac{1}{6} - \frac{3}{14} + \frac{2}{3} - \frac{2}{7}) × (-42) = -7 + 9 - 28 + 12 = -14$，所以原式 $= -\frac{1}{14}$。

15. (2025·遂宁校级月考)探究题：阅读下列材料并解决有关问题.
我们知道$|x|= \left\{\begin{array}{l} x,x＞0,\\ 0,x= 0,\\ -x,x＜0,\end{array} \right. 所以当x＞0$时,$\frac {x}{|x|}= \frac {x}{x}= 1$；当$x＜0$时,$\frac {x}{|x|}= \frac {x}{-x}= -1$.
请用上面的结论解决下列问题：
(1)已知a,b是有理数,当$ab＞0$时,$\frac {a}{|a|}+\frac {b}{|b|}=$±2；
(2)已知a,b,c是有理数,当$abc＜0$时,$\frac {a}{|a|}+\frac {b}{|b|}+\frac {c}{|c|}=$-3或1；
(3)已知a,b,c,d是有理数,当$\frac {|abcd|}{abcd}= -1$时,$\frac {a}{|a|}+\frac {b}{|b|}+\frac {c}{|c|}+\frac {d}{|d|}$的最大值是2.

答案：
(1) $\pm 2$ 解析：因为 $ab ＞ 0$，所以 $a$，$b$ 同号，即 $a ＞ 0$，$b ＞ 0$ 或 $a ＜ 0$，$b ＜ 0$，所以 $\frac{a}{|a|} + \frac{b}{|b|} = 1 + 1 = 2$ 或 $\frac{a}{|a|} + \frac{b}{|b|} = -1 -1 = -2$。综上，当 $ab ＞ 0$ 时，$\frac{a}{|a|} + \frac{b}{|b|} = \pm 2$。
(2) $-3$ 或 $1$ 解析：因为 $abc ＜ 0$，所以 $a$，$b$，$c$ 中有 $3$ 个负数或两正一负，当 $a$，$b$，$c$ 都是负数时，$\frac{a}{|a|} + \frac{b}{|b|} + \frac{c}{|c|} = -1 -1 -1 = -3$；当 $a$，$b$，$c$ 中有两正一负时，设 $a ＜ 0$，$b ＞ 0$，$c ＞ 0$，$\frac{a}{|a|} + \frac{b}{|b|} + \frac{c}{|c|} = -1 + 1 + 1 = 1$。综上，当 $abc ＜ 0$ 时，$\frac{a}{|a|} + \frac{b}{|b|} + \frac{c}{|c|}$ 的值为 $-3$ 或 $1$。
(3) $2$ 解析：因为 $\frac{|abcd|}{abcd} = -1$，所以 $a$，$b$，$c$，$d$ 中有 $1$ 个或 $3$ 个负数。当有 $1$ 个负数时，设 $a ＜ 0$，$b ＞ 0$，$c ＞ 0$，$d ＞ 0$，$\frac{a}{|a|} + \frac{b}{|b|} + \frac{c}{|c|} + \frac{d}{|d|} = -1 + 1 + 1 + 1 = 2$；当有 $3$ 个负数时，设 $a ＜ 0$，$b ＜ 0$，$c ＜ 0$，$d ＞ 0$，$\frac{a}{|a|} + \frac{b}{|b|} + \frac{c}{|c|} + \frac{d}{|d|} = -1 -1 -1 + 1 = -2$。综上，$\frac{a}{|a|} + \frac{b}{|b|} + \frac{c}{|c|} + \frac{d}{|d|}$ 的最大值是 $2$。