第15页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
9. (2025·赣州月考)在数轴上有间隔相等的四个点M,N,P,Q,所表示的数分别为m,n,p,q,其中有两个数互为相反数,若m的绝对值最大,则数轴的原点是(
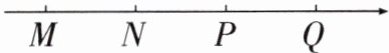
A.点N
B.点P
C.点P或点N,P的中点
D.点P或点P,Q的中点
D
)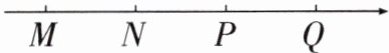
A.点N
B.点P
C.点P或点N,P的中点
D.点P或点P,Q的中点
答案:
D 解析:因为$m$的绝对值最大,所以点$M$离原点最远.因为有两个数互为相反数,所以原点在某两点之间线段的中点处,综上,原点是点$P$,$Q$的中点或点$P$.故选D.
10. (1)一个数在数轴上所对应的点向左平移6个单位长度后,得到它的相反数所对应的点,则这个数为
(2)在数轴上有A,B两点,已知点B对应的数为-2,若将原点O向左移动4个单位长度,A,B两点对应的数恰好互为相反数,则点A原来对应的数是
3
.(2)在数轴上有A,B两点,已知点B对应的数为-2,若将原点O向左移动4个单位长度,A,B两点对应的数恰好互为相反数,则点A原来对应的数是
-6
.
答案:
(1)3 解析:互为相反数的两个数表示的点到原点的距离相等,所以该点到原点的距离为3且在原点右侧,故答案为3.
(2)-6 解析:将原点$O$向左移动4个单位长度后,点$B$对应的数变为2,$A$,$B$两点对应的数恰好互为相反数,故此时点$A$对应的数为-2,将原点$O$向右移动4个单位长度,还原到原来位置,此时点$A$对应的数为-6.
(1)3 解析:互为相反数的两个数表示的点到原点的距离相等,所以该点到原点的距离为3且在原点右侧,故答案为3.
(2)-6 解析:将原点$O$向左移动4个单位长度后,点$B$对应的数变为2,$A$,$B$两点对应的数恰好互为相反数,故此时点$A$对应的数为-2,将原点$O$向右移动4个单位长度,还原到原来位置,此时点$A$对应的数为-6.
11. 化简下列各式的符号,并回答问题:
(1)$-[-(-3)]=$
$-[-(+4.5)]=$
$-\{ +[-(+5)]\} =$
$-\{ -[-(+7)]\} =$
(2)当+5前面有99个负号时,化简后的结果是
(3)计算:
$\underbrace{-(-(-…-(-3)…))}_{2n个负号,n是正整数}+(\underbrace{-(-(-…-(-1)…))}_{(2n - 1)个负号,n是正整数}).$
(1)$-[-(-3)]=$
-3
;$-[-(+4.5)]=$
4.5
;$-\{ +[-(+5)]\} =$
5
;$-\{ -[-(+7)]\} =$
-7
.(2)当+5前面有99个负号时,化简后的结果是
-5
;当-5前面有100个负号时,化简后的结果是-5
;你能总结出什么规律?规律:一个数的前面有奇数个负号,化简后的结果等于它的相反数;一个数的前面有偶数个负号,化简后的结果等于它本身.
(3)计算:
$\underbrace{-(-(-…-(-3)…))}_{2n个负号,n是正整数}+(\underbrace{-(-(-…-(-1)…))}_{(2n - 1)个负号,n是正整数}).$
$\underbrace{-(-(\cdots-(-3)\cdots))}_{2n个负号,n是正整数}+\underbrace{(-(-(\cdots-(-1)\cdots))}_{(2n - 1)个负号,n是正整数}=3 - 1 = 2$
答案:
(1)-3 4.5 5 -7
(2)-5 -5 规律:一个数的前面有奇数个负号,化简后的结果等于它的相反数;一个数的前面有偶数个负号,化简后的结果等于它本身.
(3)$\underbrace{-(-(\cdots-(-3)\cdots))}_{2n个负号,n是正整数}+\underbrace{(-(-(\cdots-(-1)\cdots))}_{(2n - 1)个负号,n是正整数}=3 - 1 = 2$
(1)-3 4.5 5 -7
(2)-5 -5 规律:一个数的前面有奇数个负号,化简后的结果等于它的相反数;一个数的前面有偶数个负号,化简后的结果等于它本身.
(3)$\underbrace{-(-(\cdots-(-3)\cdots))}_{2n个负号,n是正整数}+\underbrace{(-(-(\cdots-(-1)\cdots))}_{(2n - 1)个负号,n是正整数}=3 - 1 = 2$
12. 在数轴上点A表示的数是4,点B,C表示互为相反数的两个数,且点C与点A之间的距离为2,求数轴上A,B两点之间的距离.
答案:
如图①所示,与点$A$相距2个单位长度的点有两个,分别是数2和数6表示的点,所以点$C$表示的数是2或6.
如图②所示,当点$C$表示的数是2时,根据点$B$,$C$表示的数互为相反数可知,点$B$表示的数是-2,此时$A$,$B$两点之间的距离为6.
如图③所示,当点$C$表示的数是6时,根据点$B$,$C$表示的数互为相反数可知,点$B$表示的数是-6,此时$A$,$B$两点之间的距离为10.
综上,点$A$与点$B$两点之间的距离为6或10.


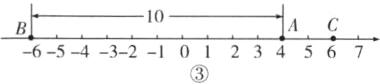
如图①所示,与点$A$相距2个单位长度的点有两个,分别是数2和数6表示的点,所以点$C$表示的数是2或6.
如图②所示,当点$C$表示的数是2时,根据点$B$,$C$表示的数互为相反数可知,点$B$表示的数是-2,此时$A$,$B$两点之间的距离为6.
如图③所示,当点$C$表示的数是6时,根据点$B$,$C$表示的数互为相反数可知,点$B$表示的数是-6,此时$A$,$B$两点之间的距离为10.
综上,点$A$与点$B$两点之间的距离为6或10.


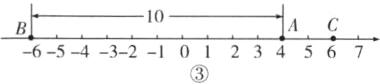
13. 已知表示互为相反数的两个数的点A,B在数轴上的距离是12,将点A沿着数轴先向右运动2s,再向左运动5s到达点C的位置. 设点A的运动速度为每秒1.5个单位长度,则点C表示的数的相反数为
-1.5或10.5
.
答案:
-1.5或10.5 解析:因为表示互为相反数的两个数的点$A$,$B$在数轴上的距离是12,所以点$A$在数轴上表示的数为6或-6.注意到$1.5×2 = 3$,$1.5×5 = 7.5$.①当点$A$在数轴上表示的数为6时,先向右运动2s,得数9,再向左运动5s,得数1.5,即点$C$在数轴上表示的数为1.5,它的相反数为-1.5;②当点$A$在数轴上表示的数为-6时,先向右运动2s,得数-3,再向左运动5s,得数-10.5,即点$C$在数轴上表示的数为-10.5,它的相反数为10.5.
14. 已知a为有理数,数轴上表示$-a$与a的点之间(包括$-a$和a)有99个整数点. (“≥”表示“大于或等于”“不小于”;“≤”表示“小于或等于”“不大于”)
(1)$-a$与a互为相反数吗?
(2)在a与$-a$之间,原点的左右两侧各有多少个整数点?
(3)a的取值范围是什么?
(1)$-a$与a互为相反数吗?
(2)在a与$-a$之间,原点的左右两侧各有多少个整数点?
(3)a的取值范围是什么?
答案:
(1)$-a$与$a$互为相反数.
(2)$-a$与$a$之间有99个整数点,则原点左右两侧各有$(99 - 1)÷2 = 49$(个)整数点.
(3)$a$对应的点到原点的距离在49到50之间,且不能等于50,则$a$的取值范围是$-50 < a ≤ -49$或$49 ≤ a < 50$.
(1)$-a$与$a$互为相反数.
(2)$-a$与$a$之间有99个整数点,则原点左右两侧各有$(99 - 1)÷2 = 49$(个)整数点.
(3)$a$对应的点到原点的距离在49到50之间,且不能等于50,则$a$的取值范围是$-50 < a ≤ -49$或$49 ≤ a < 50$.
查看更多完整答案,请扫码查看


