第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
11. 新题型 新运算 (2024·泸州模拟)从n个不同元素中取出m个元素的所有不同组合的个数,叫作从n个不同元素中取出m个元素的组合数,用符号$C_{n}^{m}$表示.已知“!”是一种数学运算符号,且$1!= 1,2!= 2×1= 2,3!= 3×2×1= 6,4!= 4×3×2×1= 24,... $,若公式$C_{n}^{m}= \frac {n!}{m!(n-m)!}(n≥m,m,n$为正整数),则$C_{7}^{5}$为____
21
.
答案:
21 解析:因为$C_{n}^{m}=\frac{n!}{m!(n-m)!}(n≥m$,n,m为正整数),所以$C_{7}^{5}=\frac{7!}{5!(7-5)!}=\frac{7×6×5×4×3×2×1}{5×4×3×2×1×2×1}=21$.
12. 计算:
(1)$[-2^{4}÷(-2\frac {2}{3})^{2}-\frac {11}{2}]÷\frac {1}{12};$
(2)$|-\frac {5}{7}|×(\frac {4}{5}-\frac {1}{3})÷(-\frac {2}{3})^{2}-(\frac {1}{2})^{2}.$
(1)$[-2^{4}÷(-2\frac {2}{3})^{2}-\frac {11}{2}]÷\frac {1}{12};$
(2)$|-\frac {5}{7}|×(\frac {4}{5}-\frac {1}{3})÷(-\frac {2}{3})^{2}-(\frac {1}{2})^{2}.$
答案:
(1)-93
(2)$\frac{1}{2}$
(1)-93
(2)$\frac{1}{2}$
13. 有个写运算符号的游戏:在“$3□ (2□ 3)□ \frac {4}{3}□ 2^{2}$”中的每个$□$内填入“+”“-”“×”“÷”中的某一个(可重复使用),然后计算结果.
(1)请计算琪琪填入符号后得到的算式:$3×(2÷3)-\frac {4}{3}÷2^{2};$
(2)嘉嘉填入符号后得到的算式是$3÷(2×3)×\frac {4}{3}□ 2^{2}$,一不小心擦掉了$□$里的运算符号,但她知道结果是$-\frac {10}{3}$,请推算出$□$内的符号.
(1)请计算琪琪填入符号后得到的算式:$3×(2÷3)-\frac {4}{3}÷2^{2};$
$\frac{5}{3}$
(2)嘉嘉填入符号后得到的算式是$3÷(2×3)×\frac {4}{3}□ 2^{2}$,一不小心擦掉了$□$里的运算符号,但她知道结果是$-\frac {10}{3}$,请推算出$□$内的符号.
-
答案:
(1)$3×(2÷3)-\frac{4}{3}÷2^{2}=3×(2÷3)-\frac{4}{3}×\frac{1}{4}=3×\frac{2}{3}-\frac{1}{3}=2-\frac{1}{3}=\frac{5}{3}$.
(2)$3÷(2×3)×\frac{4}{3}□2^{2}=3÷6×\frac{4}{3}□2^{2}=\frac{2}{3}□4=-\frac{10}{3}$.因为$\frac{2}{3}-4=-\frac{10}{3}$,所以□里的符号应是“-”.
(1)$3×(2÷3)-\frac{4}{3}÷2^{2}=3×(2÷3)-\frac{4}{3}×\frac{1}{4}=3×\frac{2}{3}-\frac{1}{3}=2-\frac{1}{3}=\frac{5}{3}$.
(2)$3÷(2×3)×\frac{4}{3}□2^{2}=3÷6×\frac{4}{3}□2^{2}=\frac{2}{3}□4=-\frac{10}{3}$.因为$\frac{2}{3}-4=-\frac{10}{3}$,所以□里的符号应是“-”.
14. 新考法 (2025·南通校级月考)取一个自然数,若它是奇数,则加上1,若它是偶数,则除以2,按此规则经过若干步的计算最终可得到1(注:计算到1结束).这个结论在数学上还没有得到证明,但举例验证都是正确的.例如,取自然数5,经过下面5步运算可得1,如图所示.如果自然数m恰好经过5步运算可得到1,那么所有符合条件的m的值有 (
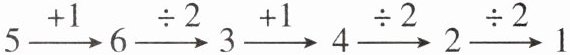
A.3个
B.4个
C.5个
D.6个
C
)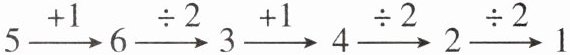
A.3个
B.4个
C.5个
D.6个
答案:
C 解析:设自然数m为第一个数,经过1步运算得到的数为第二个数,以此类推,经过5步运算得到的1为第六个数,则第五个数为$1×2=2$,第四个数为$2×2=4$.①若第三个数是奇数,则第三个数为$4-1=3$,所以第二个数为$3×2=6$,所以第一个数$m=6-1=5$或$m=6×2=12$;②若第三个数是偶数,则第三个数为$4×2=8$,所以第二个数为$8×2=16$或$8-1=7$,所以第一个数$m=16-1=15$或$m=16×2=32$或$m=7×2=14$.综上,所有符合条件的m的值为5,12,14,15,32,共有5个.故选C.
15. 观察下列各式:
$1^{3}= 1= \frac {1}{4}×1^{2}×2^{2};$
$1^{3}+2^{3}= 9= \frac {1}{4}×2^{2}×3^{2};$
$1^{3}+2^{3}+3^{3}= 36= \frac {1}{4}×3^{2}×4^{2};$
$1^{3}+2^{3}+3^{3}+4^{3}= 100= \frac {1}{4}×4^{2}×5^{2};$
…
回答下面的问题:
(1)$1^{3}+2^{3}+3^{3}+4^{3}+5^{3}=$____
(2)计算$1^{3}+2^{3}+3^{3}+... +99^{3}+100^{3}$的值;
(3)计算$11^{3}+12^{3}+... +99^{3}+100^{3}$的值.
$1^{3}= 1= \frac {1}{4}×1^{2}×2^{2};$
$1^{3}+2^{3}= 9= \frac {1}{4}×2^{2}×3^{2};$
$1^{3}+2^{3}+3^{3}= 36= \frac {1}{4}×3^{2}×4^{2};$
$1^{3}+2^{3}+3^{3}+4^{3}= 100= \frac {1}{4}×4^{2}×5^{2};$
…
回答下面的问题:
(1)$1^{3}+2^{3}+3^{3}+4^{3}+5^{3}=$____
$\frac{1}{4}×5^{2}×6^{2}$
;(2)计算$1^{3}+2^{3}+3^{3}+... +99^{3}+100^{3}$的值;
$1^{3}+2^{3}+3^{3}+... +99^{3}+100^{3}=\frac{1}{4}×100^{2}×101^{2}=25502500$
(3)计算$11^{3}+12^{3}+... +99^{3}+100^{3}$的值.
原式$=\frac{1}{4}×100^{2}×101^{2}-\frac{1}{4}×10^{2}×11^{2}=25502500-3025=25499475$
答案:
(1)$\frac{1}{4}×5^{2}×6^{2}$
(2)$1^{3}+2^{3}+3^{3}+... +99^{3}+100^{3}=\frac{1}{4}×100^{2}×101^{2}=25502500$.
(3)原式$=\frac{1}{4}×100^{2}×101^{2}-\frac{1}{4}×10^{2}×11^{2}=25502500-3025=25499475$.
(1)$\frac{1}{4}×5^{2}×6^{2}$
(2)$1^{3}+2^{3}+3^{3}+... +99^{3}+100^{3}=\frac{1}{4}×100^{2}×101^{2}=25502500$.
(3)原式$=\frac{1}{4}×100^{2}×101^{2}-\frac{1}{4}×10^{2}×11^{2}=25502500-3025=25499475$.
查看更多完整答案,请扫码查看


