第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
12. 如图是一个运算程序的示意图,若开始输入的x的值为81,我们看到第一次输出的结果为27,第二次输出的结果为9……第2024次输出的结果为
1
.
答案:
1 解析:第1次,$\frac{1}{3}×81 = 27$;第2次,$\frac{1}{3}×27 = 9$;第3次,$\frac{1}{3}×9 = 3$;第4次,$\frac{1}{3}×3 = 1$;第5次,$1 + 2 = 3$;第6次,$\frac{1}{3}×3 = 1$,…,以此类推,从第3次开始以3,1循环,因为$(2024 - 2)÷2 = 1011$,所以第2024次输出的结果为1。
13. (2025·济南期末)如图①是1个直角三角形和2个正方形,直角三角形的三条边长分别是a,b,c,其中a,b是直角边.正方形的边长分别是a,b.
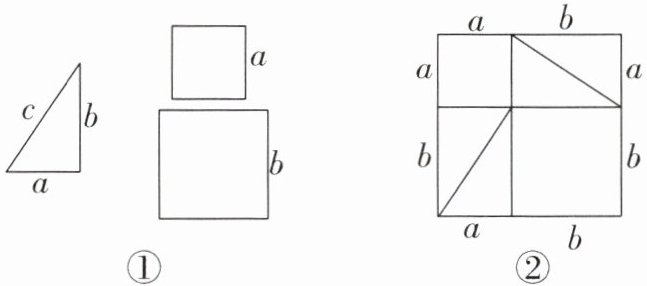
(1)将4个完全一样的直角三角形和2个正方形组成一个大正方形(如图②).用两种不同的方法列代数式表示图②中的大正方形的面积:
方法一:
(2)观察图②,试写出$(a+b)^{2},a^{2},2ab,b^{2}$这四个代数式之间的等量关系:
(3)请利用(2)中的等量关系解决问题:已知图①中三角形的面积是6,图②中大正方形的面积是49,求$a^{2}+b^{2}$的值.
(4)求$3.14^{2}+6.28×6.86+6.86^{2}$的值.

(1)将4个完全一样的直角三角形和2个正方形组成一个大正方形(如图②).用两种不同的方法列代数式表示图②中的大正方形的面积:
方法一:
$a^{2} + 2ab + b^{2}$
;方法二:$(a + b)^{2}$
.(2)观察图②,试写出$(a+b)^{2},a^{2},2ab,b^{2}$这四个代数式之间的等量关系:
$a^{2} + 2ab + b^{2} = (a + b)^{2}$
.(3)请利用(2)中的等量关系解决问题:已知图①中三角形的面积是6,图②中大正方形的面积是49,求$a^{2}+b^{2}$的值.
由于题图①中三角形的面积是6,所以$ab = 12$。因为$a^{2} + 2ab + b^{2} = (a + b)^{2}$,所以$a^{2} + b^{2} = (a + b)^{2} - 2ab = 49 - 2×12 = 25$。
(4)求$3.14^{2}+6.28×6.86+6.86^{2}$的值.
$3.14^{2} + 6.28×6.86 + 6.86^{2} = 3.14^{2} + 2×3.14×6.86 + 6.86^{2} = (3.14 + 6.86)^{2} = 10^{2} = 100$。
答案:
(1)$a^{2} + 2ab + b^{2}$ $(a + b)^{2}$
(2)$a^{2} + 2ab + b^{2} = (a + b)^{2}$
(3)由于题图①中三角形的面积是6,所以$ab = 12$。因为$a^{2} + 2ab + b^{2} = (a + b)^{2}$,所以$a^{2} + b^{2} = (a + b)^{2} - 2ab = 49 - 2×12 = 25$。
(4)$3.14^{2} + 6.28×6.86 + 6.86^{2} = 3.14^{2} + 2×3.14×6.86 + 6.86^{2} = (3.14 + 6.86)^{2} = 10^{2} = 100$。
(1)$a^{2} + 2ab + b^{2}$ $(a + b)^{2}$
(2)$a^{2} + 2ab + b^{2} = (a + b)^{2}$
(3)由于题图①中三角形的面积是6,所以$ab = 12$。因为$a^{2} + 2ab + b^{2} = (a + b)^{2}$,所以$a^{2} + b^{2} = (a + b)^{2} - 2ab = 49 - 2×12 = 25$。
(4)$3.14^{2} + 6.28×6.86 + 6.86^{2} = 3.14^{2} + 2×3.14×6.86 + 6.86^{2} = (3.14 + 6.86)^{2} = 10^{2} = 100$。
14. 已知$(-2x+1)^{5}= a_{5}x^{5}+a_{4}x^{4}+a_{3}x^{3}+a_{2}x^{2}+a_{1}x+a_{0}$是关于x的恒等式(即x取任意值时等式都成立),则$a_{1}+a_{2}+a_{3}+a_{4}+a_{5}= $
-2
.
答案:
−2 解析:当$x = 0$时,$a_{0} = 1$;当$x = 1$时,$a_{5} + a_{4} + a_{3} + a_{2} + a_{1} + a_{0} = -1$,则$a_{1} + a_{2} + a_{3} + a_{4} + a_{5} = -2$。
15. 在学习代数式的值时,介绍了计算程序:用“$□$”表示数据输入、输出框;用“$□$”表示数据处理和运算框;用“$\lozenge$”表示数据判断框(根据条件决定执行两条路径中的某一条).
(1)①如图①,当输入$x= -2$时,输出$y= $____;
②如图②,第一个运算框“$□$”内应填____;第二个运算框“$□$”内应填____.
(2)①如图③,当输入$x= -1$时,输出$y= $____;
②如图④,当输出$y= 37$时,输入的值$x= $____.
(3)为鼓励节约用水,政府决定对用水实行“阶梯价”:
当每月用水量不超过15t(含15t)时,以2元/t的价格收费;当每月用水量超过15t时,超过部分以3元/t的价格收费.请设计出一个“计算程序”,使得输入数为每月用水量x,输出数为水费y.

(1)①如图①,当输入$x= -2$时,输出$y= $____;
②如图②,第一个运算框“$□$”内应填____;第二个运算框“$□$”内应填____.
(2)①如图③,当输入$x= -1$时,输出$y= $____;
②如图④,当输出$y= 37$时,输入的值$x= $____.
(3)为鼓励节约用水,政府决定对用水实行“阶梯价”:
当每月用水量不超过15t(含15t)时,以2元/t的价格收费;当每月用水量超过15t时,超过部分以3元/t的价格收费.请设计出一个“计算程序”,使得输入数为每月用水量x,输出数为水费y.

答案:
(1)①−9 ②×5 −3
(2)①−43 ②42或−6 解析:①当$x = -1$时,$y = -1×2 - 5 = -7 > -20$,$-7×2 - 5 = -19 > -20$,$-19×2 - 5 = -43 < -20$,故答案为-43。②分为两种情况:当$x > 0$时,$x - 5 = 37$,解得$x = 42$;当$x < 0$或$x = 0$时,$x^{2} + 1 = 37$,解得$x = -6$(舍去正数)。故答案为42或-6。
(3)因为当每月用水量不超过15t(含15t)时,以2元/t的价格收费;当每月用水量超过15t时,超过部分以3元/t 的价格收费,所以水费收费分两种情况:$x ≤ 15$和$x > 15$,分别计算。所以可以设计计算程序如图所示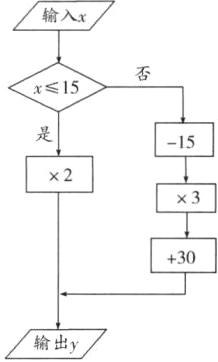
(1)①−9 ②×5 −3
(2)①−43 ②42或−6 解析:①当$x = -1$时,$y = -1×2 - 5 = -7 > -20$,$-7×2 - 5 = -19 > -20$,$-19×2 - 5 = -43 < -20$,故答案为-43。②分为两种情况:当$x > 0$时,$x - 5 = 37$,解得$x = 42$;当$x < 0$或$x = 0$时,$x^{2} + 1 = 37$,解得$x = -6$(舍去正数)。故答案为42或-6。
(3)因为当每月用水量不超过15t(含15t)时,以2元/t的价格收费;当每月用水量超过15t时,超过部分以3元/t 的价格收费,所以水费收费分两种情况:$x ≤ 15$和$x > 15$,分别计算。所以可以设计计算程序如图所示

查看更多完整答案,请扫码查看


