《2025年学霸题中题七年级数学上册苏科版》

1. 四个同学研究一列数：1,-3,5,-7,9,-11,13,…,按照此规律,他们得出第n个数分别如下,你认为正确的是(D)
A.$2n - 1$
B.$1 - 2n$
C.$(-1)^n(2n - 1)$
D.$(-1)^{n + 1}(2n - 1)$

答案： D

2. (2023·牡丹江中考)观察下面两行数：
1,5,11,19,29,…
1,3,6,10,15,…
取每行数的第7个数,计算这两个数的和是(C)
A.92
B.87
C.83
D.78

答案： C 解析：第一行的数规律为 $n^{2}+n - 1$，第二行的数规律为 $\frac{n^{2}+n}{2}$，所以第一行的第 7 个数为 $7^{2}+7 - 1 = 55$，第二行的第 7 个数为 $\frac{7^{2}+7}{2}=28$，所以 $55 + 28 = 83$，故选 C.

3. (2023·常德中考)观察图中的数表(横排为行,竖排为列),按数表中的规律,分数$\frac{20}{2023}$若排在第a行第b列,则$a - b$的值为(C)
A.2003
B.2004
C.2022
D.2023

答案： C 解析：观察数表中的规律发现，分数的分子是几，则必在第几列；只有第一列的分数，分母与其所在行数一致，故 $\frac{20}{2023}$ 在第 20 列，即 $b = 20$；向前递推到第 1 列时，分数为 $\frac{20 - 19}{2023 + 19}=\frac{1}{2042}$，故分数 $\frac{20}{2023}$ 与分数 $\frac{1}{2042}$ 在同一行，即在第 2042 行，则 $a = 2042$，所以 $a - b = 2042 - 20 = 2022$. 故选 C.

4. (广西中考)观察下列一行数：4,1,-8,1,16,1,-32,1,64,1,-128,1,…,则第19个数与第20个数的和为-2047。

答案： -2047 解析：观察可发现规律：这列数的第偶数个数都是 1，第奇数个数是 $(-2)^{\frac{n + 1}{2}+1}$，所以当 $n = 19$ 时，这个数为 $(-2)^{\frac{19 + 1}{2}+1}=-2048$，当 $n = 20$ 时，这个数为 1，所以第 19 个数与第 20 个数的和为 $-2048 + 1 = -2047$.

5. (2024·潍坊中考)将连续的正整数排成如图所示的数表。记$a_{(i,j)}$为数表中第i行第j列位置的数字,如$a_{(1,2)} = 4$,$a_{(3,2)} = 8$,$a_{(5,4)} = 22$。若$a_{(m,n)} = 2024$,则$m = $45,$n = $2。

答案： 45 2 解析：由题图中排布可知，当正整数为 $k^{2}$ 时，若 $k$ 为奇数，则 $k^{2}$ 在第 $k$ 行，第 1 列，下一个数在下一行，上一个数在第 2 列；若 $k$ 为偶数，则 $k^{2}$ 在第 1 行，第 $k$ 列，下一个数在下一列，上一个数在第 2 行；因为 $a_{(m,n)} = 2024 = 2025 - 1 = 45^{2} - 1$，而 $2025 = 45^{2}$ 在第 45 行，第 1 列，所以 2024 在第 45 行，第 2 列，所以 $m = 45$，$n = 2$.

6. 观察多项式：$2a + b$,$4a^2 - b^3$,$6a^3 + b^5$,$8a^4 - b^7$,…,根据规律,第6个多项式为(B)
A.$12a^6 + b^{11}$
B.$12a^6 - b^{11}$
C.$10a^6 - b^{13}$
D.$10a^6 - b^{11}$

答案： B

7. “数形结合”是一种重要的数学思维,观察下面的图形和算式：
$1 = 1 = 1^2$；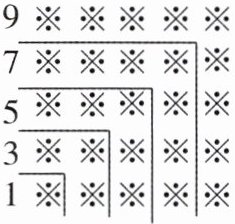
$1 + 3 = 4 = 2^2$；
$1 + 3 + 5 = 9 = 3^2$；
$1 + 3 + 5 + 7 = 16 = 4^2$；
$1 + 3 + 5 + 7 + 9 = 25 = 5^2$；
…
解答下列问题：请用上面得到的规律计算：$21 + 23 + 25 + 27 + … + 101 = $B
A.2601
B.2501
C.2400
D.2419

答案： B 解析：根据图形和算式的变化发现规律：$1 + 3 + 5 + 7 + 9 + \cdots + 19 = 100 = 10^{2}$，$1 + 3 + 5 + 7 + 9 + \cdots + 19 + 21 + 23 + 25 + 27 + \cdots + 101 = 51^{2}$，所以 $21 + 23 + 25 + 27 + \cdots + 101 = 51^{2} - 10^{2} = 2501$. 故选 B.

8. (2024·宁夏中考)观察下列等式：
第1个：$1×2 - 2 = 2^2×0$；第2个：$4×3 - 3 = 3^2×1$；
第3个：$9×4 - 4 = 4^2×2$；第4个：$16×5 - 5 = 5^2×3$。
按照以上规律,第n个等式为$n^{2}(n + 1)-(n + 1)=(n + 1)^{2}(n - 1)$。

答案： $n^{2}(n + 1)-(n + 1)=(n + 1)^{2}(n - 1)$ 解析：观察算式可知，序号的平方乘序号加 1 的积减去序号加 1 的结果等于序号加 1 的平方乘序号减 1 的差，所以第 $n$ 个等式为 $n^{2}(n + 1)-(n + 1)=(n + 1)^{2}(n - 1)$.

9. 如图中的程序所示,输入一个整数便会按程序进行计算：

设输入的x值为18,那么根据程序,第1次计算的结果为9；第2次计算的结果为4；…；这样下去第5次计算的结果是-4；第299次计算的结果是-4。

答案： -4 -4 解析：输入 18，依次得到的结果为 9，4，2，1，-4，-2，-1，-6，-3，-8，-4，-2，-1，…，显然除去前 4 次结果外，从第 5 次的结果 -4 开始，每 6 次一循环，而 $(299 - 4)÷6 = 49\cdots\cdots1$，故第 299 次计算的结果为 -4.

10. 观察下列各式：$-1×\frac{1}{2} = -1 + \frac{1}{2}$,$-\frac{1}{2}×\frac{1}{3} = -\frac{1}{2} + \frac{1}{3}$,$-\frac{1}{3}×\frac{1}{4} = -\frac{1}{3} + \frac{1}{4}$,…。
(1)猜想：$-\frac{1}{100}×\frac{1}{101} = $$-\frac{1}{100}+\frac{1}{101}$；(写成和的形式)
(2)你发现的规律是$-\frac{1}{n}×\frac{1}{n + 1} = $$-\frac{1}{n}+\frac{1}{n + 1}$；(n为正整数)
(3)用规律计算：$(-1×\frac{1}{2}) + (-\frac{1}{2}×\frac{1}{3}) + (-\frac{1}{3}×\frac{1}{4}) + … + (-\frac{1}{999}×\frac{1}{1000}) + (-\frac{1}{1000}×\frac{1}{1001}) = $$-\frac{1000}{1001}$。

答案：
(1) $-\frac{1}{100}+\frac{1}{101}$
(2) $-\frac{1}{n}+\frac{1}{n + 1}$
(3) $-\frac{1000}{1001}$ 解析：原式 $=-1+\frac{1}{2}-\frac{1}{2}+\frac{1}{3}-\frac{1}{3}+\frac{1}{4}-\cdots-\frac{1}{1000}+\frac{1}{1001}=-1+\frac{1}{1001}=-\frac{1000}{1001}$.