《2025年学霸题中题七年级数学上册苏科版》

10.(1)把一根木棒锯成3段需要12 min,那么把它锯成10段需要54min.
(2)一口井深10 m,一只蜗牛从井底向上爬,它白天可向上爬3 m,夜间向下滑2 m,这只蜗牛第8天可以爬出井口.
(3)妈妈使用一个平底锅烙饼,这个平底锅每次只能放2张饼,1张饼要烙两面,烙熟一面要3 min,烙熟3张饼至少需要9min.

答案：
(1)54　解析:根据将木棒锯成3段要锯2次,可得锯1次的时间为12÷2=6(min),将木棒锯成10段要锯9次,需要的时间为6×9=54(min).　　
(2)8　解析:我们把“白天向上爬3m,夜间向下滑2m”看作一个循环.因为蜗牛一个昼夜最多可以向上爬1m,所以最后1个循环是不完整的，用总长度减去最后1个白天向上爬的米数，然后再除以一个循环爬的米数，算出需要多少天，最后再加上最后1个白天即可.(10−3)÷(3−2)=7÷1=7(天),7+1=8(天).即这只蜗牛第8天可以爬出井口.　　
(3)9　解析:充分利用平底锅，尽量使每次都有2张饼在烙.3张饼可以用序号1,2,3表示,列出安排表如下:| | 饼 | 所用时间 | | --- | --- | --- | | 第一次烙 | 1 正、2 正 | 3 min | | 第二次烙 | 1 反、3 正 | 3 min | | 第三次烙 | 2 反、3 反 | 3 min | 3+3+3=9(min),所以烙熟3张饼至少需要9min.

11.如图为阿辉、小燕一起到商店分别买了数杯饮料与在家分饮料的经过.若每杯饮料的价格均相同,则根据图中的对话,阿辉买了多少杯饮料?

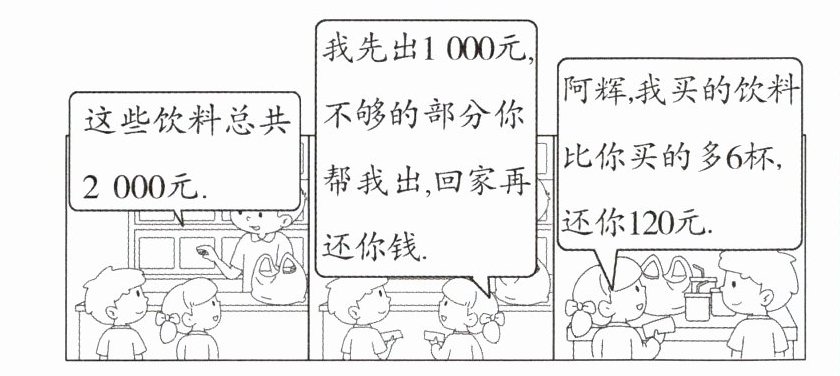
答案： 因为小燕先付1000元，又还给阿辉120元，所以小燕买饮料花了1000+120=1120(元),阿辉花了2000−1120=880(元),所以小燕比阿辉多付了1120−880=240(元).因为小燕比阿辉多买了6杯饮料，所以每杯饮料的价格为240÷6=40(元),所以阿辉买了880÷40=22(杯)饮料.

12.(北京中考改编)某公园划船项目收费标准如下:

某班18名同学一起去该公园划船,若每人划船的时间均为1 h,且每条船均坐满,则租船的总费用最低为______元.
380

答案： 380　解析:由题意列表如下:| 两人船数量 | 四人船数量 | 六人船数量 | 八人船数量 | 费用/元 | | --- | --- | --- | --- | --- | | 0 | 1 | 1 | 1 | 380 | | 0 | 0 | 3 | 0 | 390 | | 0 | 3 | 1 | 0 | 430 | | 1 | 0 | 0 | 2 | 390 | | 1 | 1 | 2 | 0 | 450 | | 1 | 2 | 0 | 1 | 440 | | 1 | 4 | 0 | 0 | 490 | | 2 | 0 | 1 | 1 | 460 | | 2 | 2 | 1 | 0 | 510 | | 3 | 1 | 0 | 1 | 520 | | 3 | 0 | 2 | 0 | 530 | | 3 | 3 | 0 | 0 | 570 | | 4 | 1 | 1 | 0 | 590 | | 5 | 0 | 0 | 1 | 600 | | 5 | 2 | 0 | 0 | 650 | | 6 | 0 | 1 | 0 | 670 | | 7 | 1 | 0 | 0 | 730 | | 9 | 0 | 0 | 0 | 810 | 所以当租1条四人船、1条六人船、1条八人船时总费用最低，最低费用为380元.

13.概念:如果一个n×n矩阵(教材中表现为方格图)的每行、每列及两条对角线的元素之和都相等,且这些元素都是从1到n的自然数,这样的矩阵就称为n阶幻方.有关幻方问题的研究在我国已流传了两千多年,这是一类形式独特的填数字问题.
下面介绍一种构造三阶幻方的方法——杨辉法.口诀(如图):“九子斜排,上下对易,左右相更,四维挺出.”

(1)将左边方格中的9个数填入右边方格中,使每一行、每一列、每条对角线上的三个数之和都相等.

(2)将9个连续自然数填入方格内,使每一行、每一列、每条对角线上的三个数之和都等于60.

答案：

(1)填数如图①.(填法不唯一)　　　　　　　 　　　
(2)设9个连续自然数中的第5个数为x,由已知可得9x = 60×3，解得x = 20。所以这连续的九个数为16，17，18，19，20，21，22，23，24。填数如图②。（填法不唯一）